R语言对混合分布中的不可观测与可观测异质性因子分析

今天上午，在课程中，我们讨论了利率制定中可观察和不可观察异质性之间的区别（从经济角度出发）。

为了说明这一点，我们看了以下简单示例。让 X 代表一个人的身高。考虑以下数据集

可下载资源

> Davis[12,c(2,3)]=Davis[12,c(3,2)]

在这里，关注变量是给定人的身高，

> X=Davis$height

如果我们看直方图，我们有

> hist(X,col="light green", border="white",proba=TRUE,xlab="",main="")

This image has an empty alt attribute; its file name is image.png

专栏

精算科学

关于结合数学、统计方法以及程序语言对经济活动来做风险分析、评估的见解。

探索专栏 ➔

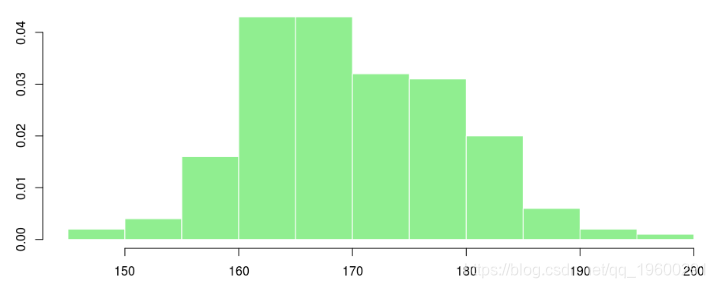
我们可以假设我们具有高斯分布吗？

在这里，如果我们拟合高斯分布，将其绘制出来，并添加基于核的估计量，我们将得到

> (param <- fitdistr(X,"normal")$estimate) 
> f1 <- function(x) dnorm(x,param[1],param[2]) 
> x=seq(100,210,by=.2) 
> lines(x,f1(x),lty=2,col="red") 
> lines(density(X))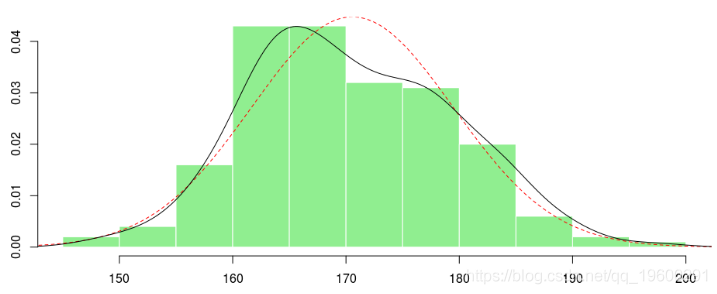

如果看那条黑线，可能会想到一种混合分布，例如

当我们有一个获得混合分布不可观察的异质性因子：概率 p1，一个随机变量 $\mathcal{N}(\mu_1,\sigma_1^2)$ ，概率p2，一个随机变量 $\mathcal{N}(\mu_2,\sigma_2^2)$ 。我们可以使用例如


> (param12 <- c(mix$lambda[1],mix$mu,mix$sigma)) 
[1] 0.4002202 178.4997298 165.2703616 6.3561363 5.9460023

如果我们绘制两个高斯分布的混合图，我们得到


> lines(x,f2(x),lwd=2, col="red") lines(density(X))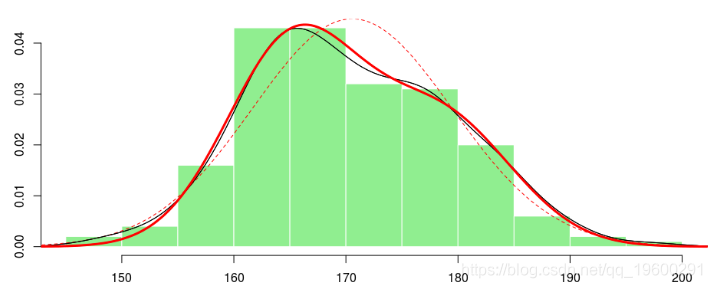

不错。实际上，我们可以尝试使用自己的代码最大限度地提高可能性，


> bvec <- c(0,-1,0,0)
> constrOptim(c(.5,160,180,10,10), logL, NULL, ui = Amat, ci = bvec)$par

[1]   0.5996263 165.2690084 178.4991624   5.9447675   6.3564746

在这里，我们包括一些约束，以保证概率属于单位间隔，并且方差参数保持正值。

进一步来说，如果我们假设基础分布具有相同的方差，即

$X\sim p_1\cdot\mathcal{N}(\theta_1,\sigma^2)+p_2\cdot\mathcal{N}(\theta_2,\sigma^2)$

在这种情况下，我们必须使用之前的代码，并进行一些小的更改，


> (param12c= constrOptim(c(.5,160,180,10), logL, NULL, ui = Amat, ci = bvec)$par)

[1]   0.6319105 165.6142824 179.0623954   6.1072614

最受欢迎的见解

1.R语言绘制生存曲线估计|生存分析|如何R作生存曲线图

2.R语言生存分析可视化分析

3.R语言如何在生存分析与Cox回归中计算IDI，NRI指标

4.r语言中使用Bioconductor 分析芯片数据

5.R语言生存分析数据分析可视化案例

6.r语言ggplot2误差棒图快速指南

7.R 语言绘制功能富集泡泡图

8.R语言如何找到患者数据中具有差异的指标？（PLS—DA分析）

9.R语言中的生存分析Survival analysis晚期肺癌患者4例

如果我们不能观察到异质性因素，这就是我们可以做的。我们实际上在数据集中有一些信息。例如，我们具有人的性别。现在，如果我们查看每个性别的身高直方图，以及基于内核的每个性别的身高密度估计量，

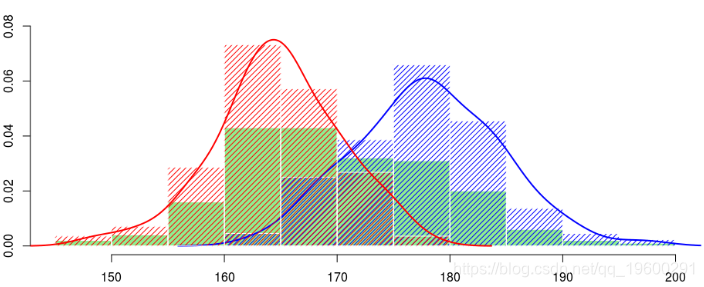
因此，看起来男性的身高和女性的身高是不同的。也许我们可以使用实际观察到的变量来解释样本中的异质性。在形式上，这里的想法是考虑具有可观察到的异质性因素的混合分布：性别，

现在，我们对以前称为类[1]和[2]的解释是：男性和女性。在这里，估算参数非常简单，


sex=="F"
      mean         sd 
164.714286   5.633808 
sex=="M"
      mean         sd 
178.011364   6.404001

如果我们绘制密度，我们有

> lines(x,f4(x),lwd=3,col="blue")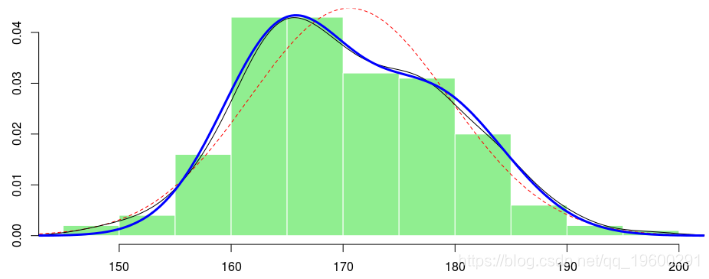

如果再次假设相同的方差怎么办？即，模型变为

然后，一个自然的想法是根据以前的计算得出方差的估计量


> s
[1] 6.015068

再一次，可以绘制相关的密度，

> lines(x,f5(x),lwd=3,col="blue")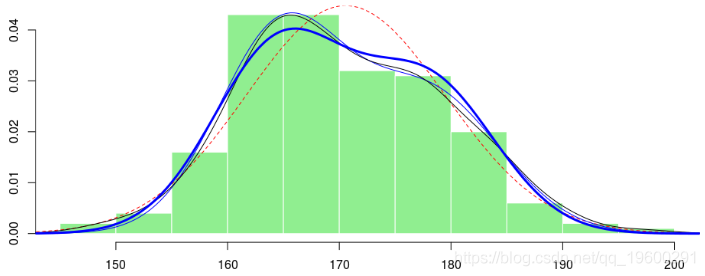

现在，如果我们仔细考虑一下我们所做的事情，那仅仅是对一个因素（人的性别）的线性回归，

$\varepsilon\sim\mathcal{N}(0,\sigma^2)$

实际上，如果我们运行代码来估算此线性模型，


Residuals:
     Min       1Q   Median       3Q      Max 
-16.7143  -3.7143  -0.0114   4.2857  18.9886 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 164.7143     0.5684  289.80   <2e-16 ***
sexM         13.2971     0.8569   15.52   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6.015 on 198 degrees of freedom
Multiple R-squared:  0.5488,	Adjusted R-squared:  0.5465 
F-statistic: 240.8 on 1 and 198 DF,  p-value: < 2.2e-16

我们得到的均值和方差的估计与之前获得的估计相同。因此，正如今天上午在课堂上提到的，如果您有一个不可观察的异质性因子，我们可以使用混合模型来拟合分布，但是如果您可以得到该因子的替代，这是可观察的，则可以运行回归。

可下载资源

关于作者

Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。

本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。

非常感谢您阅读本文，如需帮助请联系我们！