资本资产定价模型（CAPM） 是用于确定是否在一个特定资产的投资是值得的。
本质上，问题是：“该资产的回报是否值得投资？”
在本教程中，我们将应用CAPM模型，使用多元回归模型查看特定股票是否值得投资。
在CAPM模型中，股票的期望收益率为：
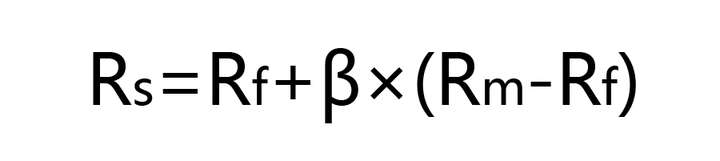
式中，Rs代表该股票的期望收益率，Rf代表无风险利率，Rm代表市场预期收益率，Rm-Rf被称为市场风险溢价，β是风险系数。
接下来，我们对公式逐项进行解析。
无风险收益率Rf
在证券界，通常将期限小于三个月的短期贴现国债视为无风险证券。因为三个月的期限很短，在这期间市场利率波动对债券的影响很小，其收益基本是恒定的，所以可以认为是无风险的。 然而结合我国的情况，目前还没有三个月的国库券，因此无风险利率一般参照短期存款利率。
市场风险溢价Rm-Rf
作为一个投资者，我们选择把钱投资股票而非存进银行，是因为股市的回报要高于银行。市场风险溢价就是用来衡量二者之间差值的工具。换言之，一旦市场风险溢价为负，那CAPM模型也就失去意义了。不过因为股票具有风险，因此某一时期市场溢价出现负值也不是没有可能的。
风险系数β
β系数反映了单个证券与整体市场组合的联动性，用来衡量单个证券的风险。
β>1：股票收益与股指同向变化，且变化比股指快；
β=1：股票收益与股指同向变化，且变化速度相同；
0<β<1：股票收益与股指同向变化，且变化比股指慢；
β=0：无系统风险；
β<0：股票收益永远与股指反向变化。
CAPM：公式
经济学就是权衡取舍。根据CAPM公式，基本上将股票或任何类型的资产类别与相对无风险的资产（通常是政府债券）进行比较，因为这些资产的违约概率非常低。CAPM公式如下
- E（Ri）是期望收益率。
- Rf是无风险资产，通常是政府债券。
- βi 系数反映了单个证券与整体市场组合的联动性，用来衡量单个证券的风险。
- E（Rm）-Rf被认为是 风险溢价。
我们可以用下图以图形方式表示CAPM模型
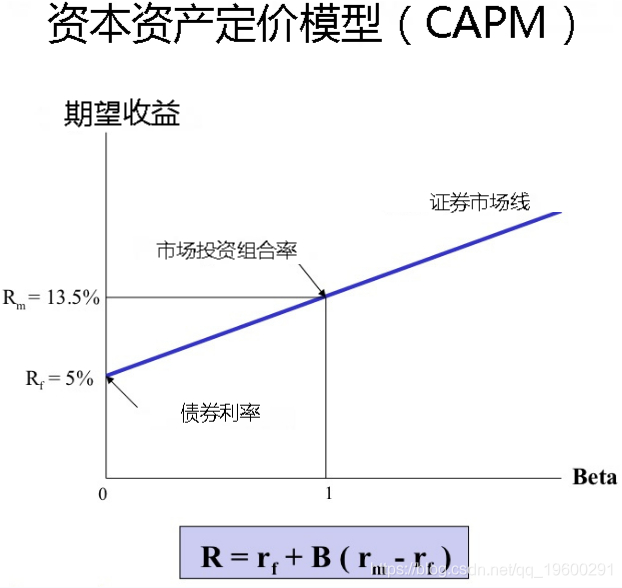
在 证券市场线（SML）上的有效组合或者是单一的无风险资产或行是无风险资产与市场组合的组合。因此，资本市场线不能解释所有的单一证券或者是只有风险证券组合的期望收益率和风险之间的关系。
我们的目标是使用线性回归找到βi的值。
数据
我们将使用数据来查找每只股票的beta。
kable(head(capm, 11), format = 'html')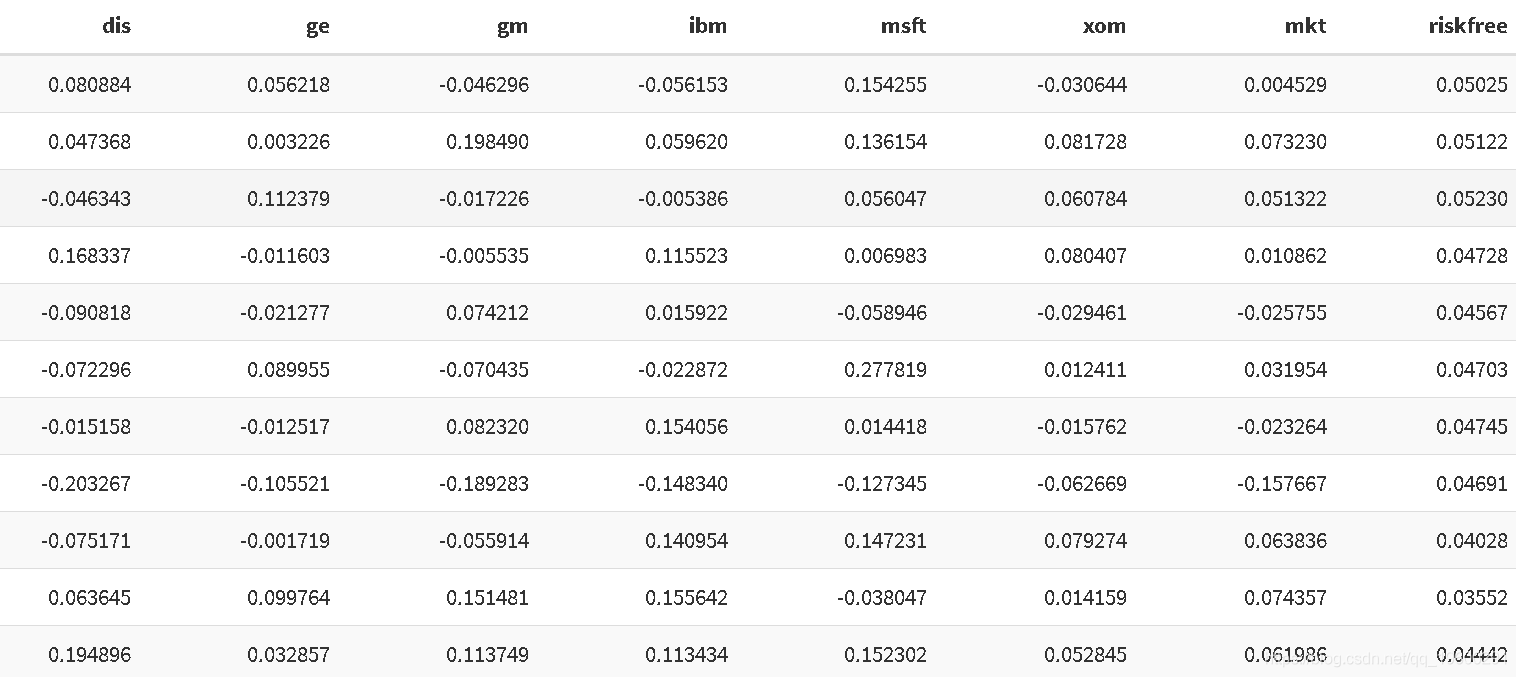 
1. ## dis ge gm
2. ## Min. :-0.267794 Min. :-0.234902 Min. :-0.389313
3. ## 1st Qu.:-0.043638 1st Qu.:-0.032974 1st Qu.:-0.076167
4. ## Median : 0.005858 Median :-0.004716 Median :-0.013017
5. ## Mean : 0.001379 Mean : 0.001361 Mean :-0.009081
6. ## 3rd Qu.: 0.047858 3rd Qu.: 0.040096 3rd Qu.: 0.068138
7. ## Max. : 0.241453 Max. : 0.192392 Max. : 0.276619
8. ## ibm msft xom
9. ## Min. :-0.226453 Min. :-0.343529 Min. :-0.116462
10. ## 1st Qu.:-0.038707 1st Qu.:-0.056052 1st Qu.:-0.028031
11. ## Median : 0.006482 Median : 0.003996 Median : 0.003309
12. ## Mean : 0.008332 Mean : 0.008557 Mean : 0.010488
13. ## 3rd Qu.: 0.051488 3rd Qu.: 0.056916 3rd Qu.: 0.041534
14. ## Max. : 0.353799 Max. : 0.407781 Max. : 0.232171
15. ## mkt riskfree
16. ## Min. :-0.184726 Min. :0.000025
17. ## 1st Qu.:-0.022966 1st Qu.:0.001376
18. ## Median : 0.010952 Median :0.002870
19. ## Mean : 0.002511 Mean :0.002675
20. ## 3rd Qu.: 0.037875 3rd Qu.:0.003904
21. ## Max. : 0.083925 Max. :0.005195
根据我们的数据，我们有六只股票，我们必须决定这些股票是否值得投资。不幸的是，由于我们必须首先将数据转换为公式（1），因此我们不能仅仅拟合回归模型。我们将必须根据已有变量来计算新变量。
我们需要计算每只股票的风险溢价E（Rm）-Rf。
risk.premium <- mkt -riskfree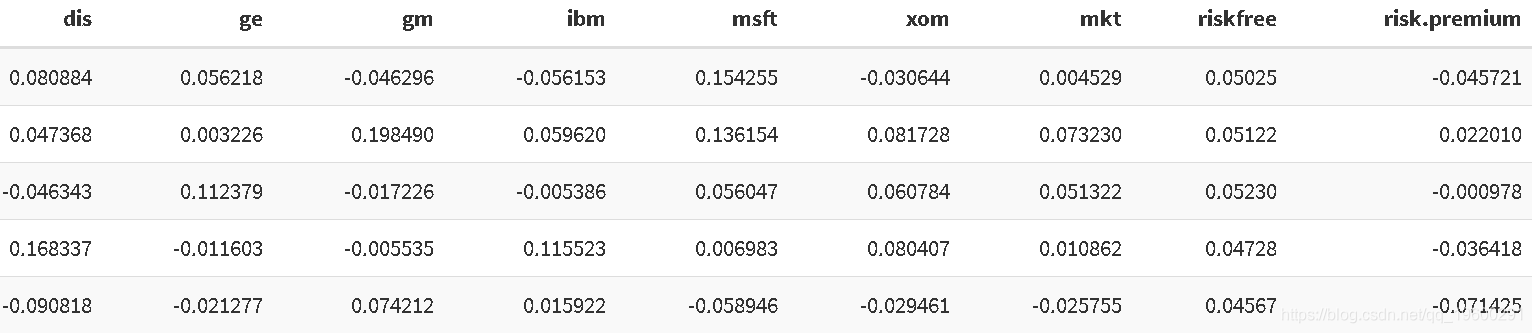
随时关注您喜欢的主题
我们看一下股票（msft）的散点图。
ggplot(aes(y = msft, x = risk.premium)) + geom_point(col='blue') + xlab('风险溢价') +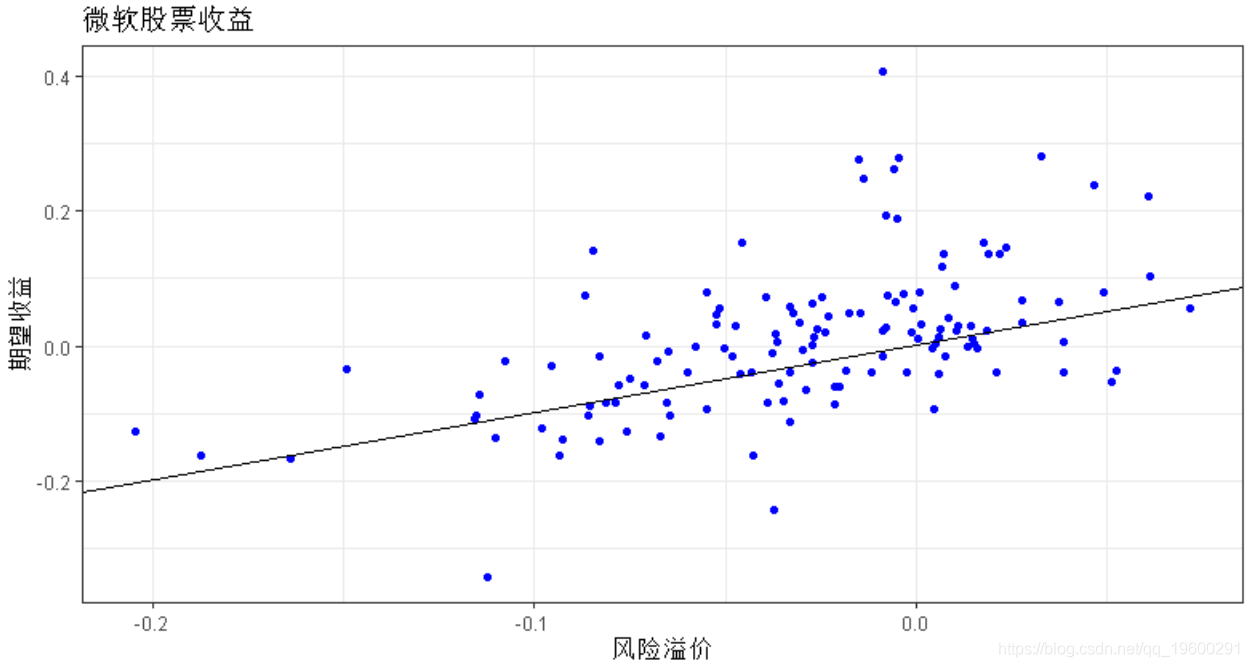 
值得注意的是，风险溢价越高，期望收益就应该越大。否则，投资具有期望低回报的高风险资产并不是明智之举，因为这会导致损失。
拟合模型
现在我们可以开始拟合我们的回归模型。首先，我们必须将数据分为训练集和测试集。
1. # 我们将需要为所有六只股票创建回归模型。
2. dis.fit <- lm(dis ~ riskfree + risk.premium, data = capm)
5. # 建立表格
7. kable(df, format = 'html') %>%
我们如何解释风险溢价的价值？风险溢价越高，资产的波动性或风险就越大，因此，投资者应获得可证明资产风险合理的回报，以弥补损失。
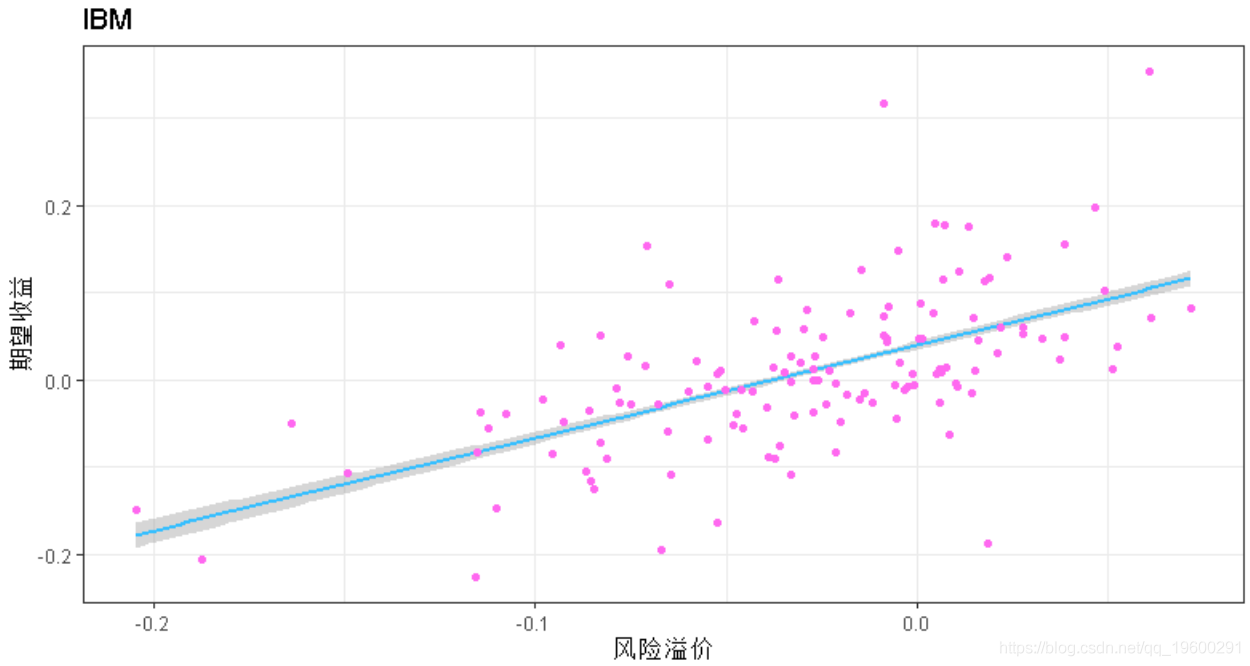
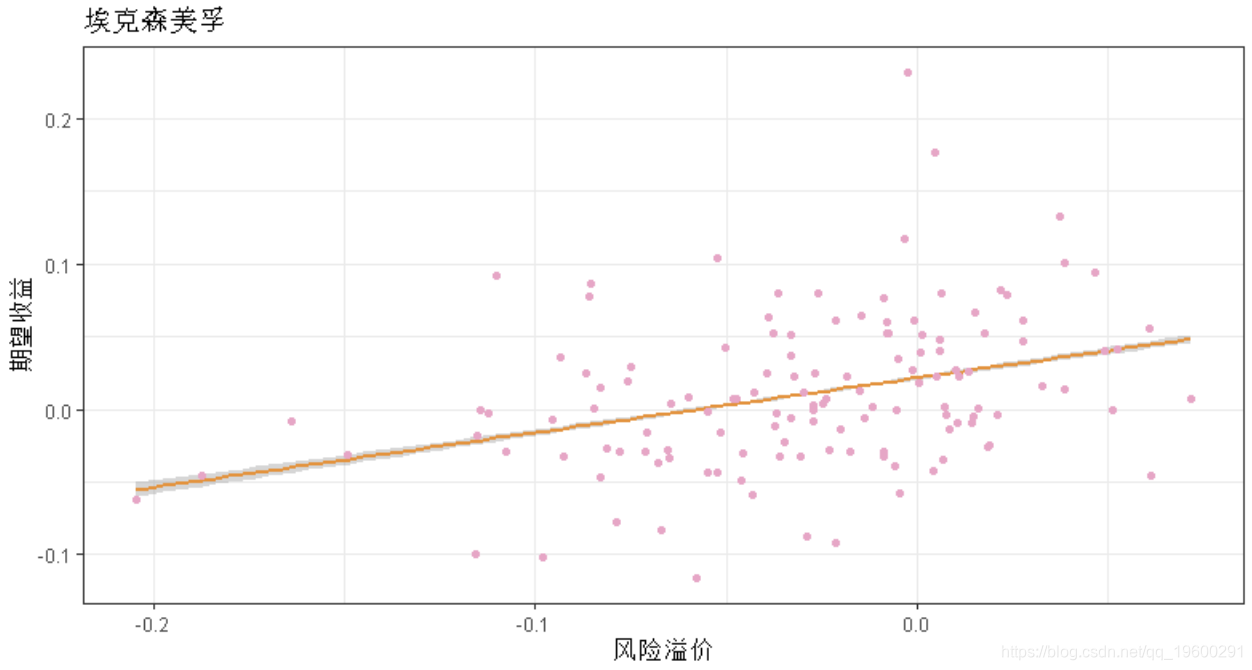
现在我们已经估计了beta，可以使用公式（1）计算每只股票的期望收益。
# 将预测添加到原始数据集
capm$dis.predict <- dis.predict拟合回归线
ggplot aes(y = dis.predict, x = risk.premium) +
geom_smooth(col='tomato2', method='lm') +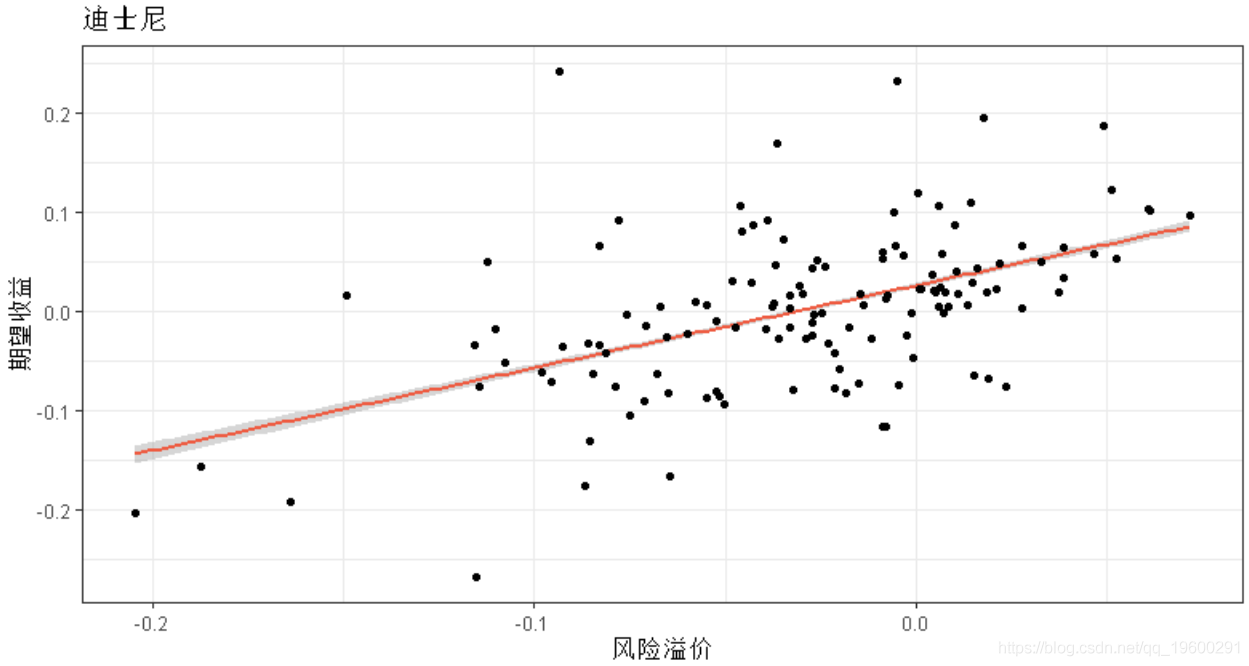 
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
专题：Python实现贝叶斯线性回归与MCMC采样数据可视化分析2实例|附代码数据
视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析
Python谷歌商店Google Play APP评分预测：LASSO、多元线性回归、岭回归模型对比研究
Python+AI提示词出租车出行轨迹：梯度提升GBR、KNN、LR回归、随机森林融合预测及贝叶斯概率异常检测研究
