动量和马科维茨投资组合模型使 均值方差优化 组合成为可行的解决方案。
通过建议并测试：
可下载资源
#*****************************************************************
# 加载历史数据
#*****************************************************************
load.packages('quantmod')
# 加载保存的原始数据
#
load('raw.Rdata')
getSymbols.extra(N8.tickers, src = 'yahoo', from = '1970-01-01', env = data, raw.data =
for(i in data$symbolnames) data[[i]] = adjustOHLC(data[[i]]接下来，让我们测试函数
×
在投资的过程中，大家会常常听到“资产配置”、“投资组合”等术语，这些术语的含义都是通过分散化投资的方式来降低投资过程中所存在的风险。那么问题来了，如何定义投资风险，以及如何分散化投资才能实现收益与风险的最优配比？上世纪50年代，美国经济学家马科维茨首次利用数理分析的方法提出了风险与收益的精确定义，即基于均值方差的投资组合理论，该理论奠定了现代金融投资组合理论的基础。
马科维茨投资组合理论认为投资单只股票的风险可以分为系统性风险和非系统性风险，系统性风险概括来说就是市场风险，例如宏观经济变动或政策变动。非系统性风险指的是特定风险，例如公司破产、财务造假等特定事件，这种风险对于个股的冲击尤其之大，但只要想办法增加组合中的股票数目，该类风险可以被分散掉，这也是我们俗称的“鸡蛋不要放在一个篮子里”。
在马科维茨投资组合理论中，其利用组合方差和均值分别来定义组合风险与收益，其表达式为：
#*****************************************************************
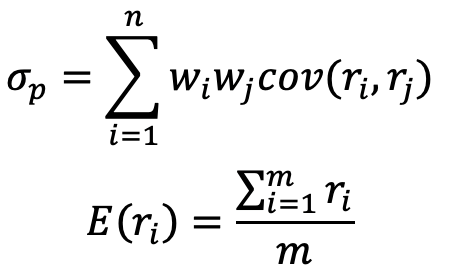
# 运行测试，每月数据
#*****************************************************************
plot(scale.one(data$prices))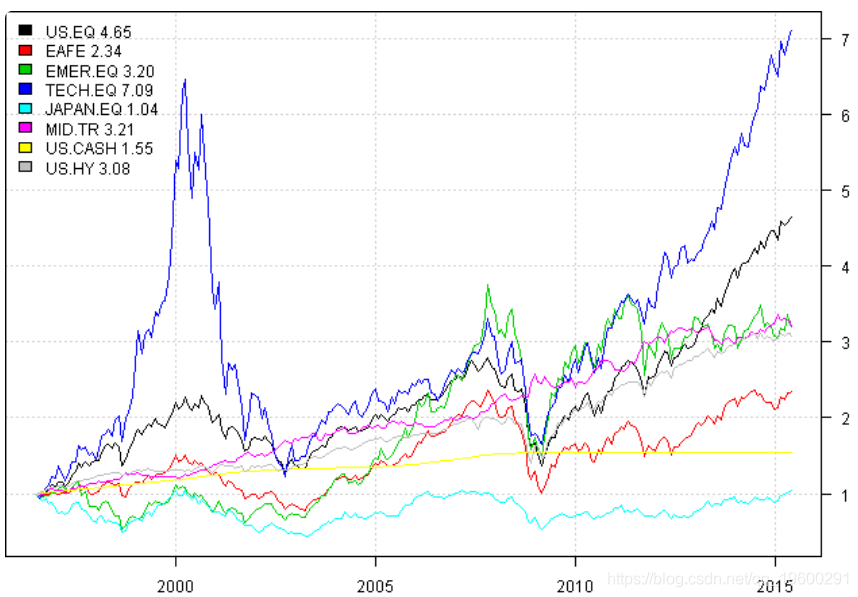
prices = data$prices
plotransition(res[[1]]['2013::'])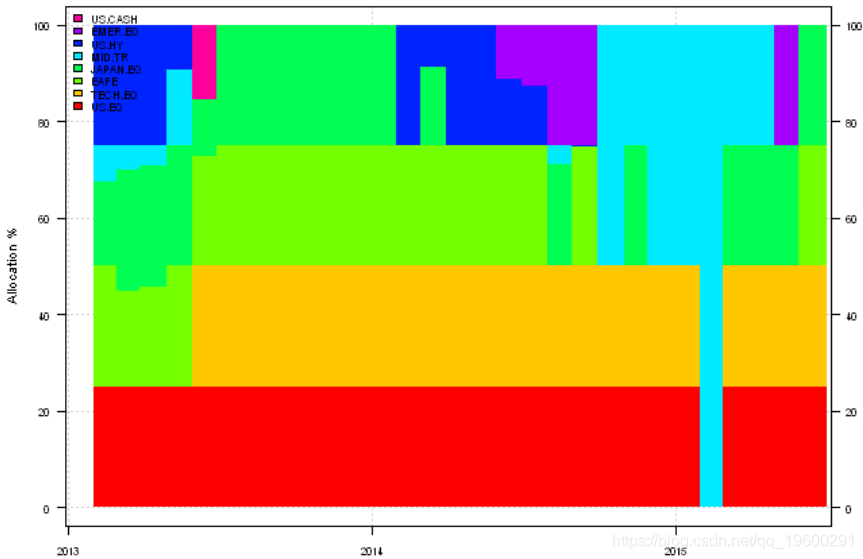
接下来，让我们创建一个基准并设置用于所有测试。
#*****************************************************************
# 建立基准
#*****************************************************************
models = list()
commission = list(cps = 0.01, fixed = 10.0, percentage = 0.0)
data$weight[] = NA
model = brun(data, clean.signal=T, 接下来，让我们获取权重，并使用它们来进行回测
#*****************************************************************
# 转换为模型结果
#*****************************************************************
CLA = list(weight = res[[1]], ret = res[[2]], equity = cumprod(1 + res[[2]]), type = "weight")
obj = list(weights = list(CLA = res[[1]]), period.ends我们可以复制相同的结果
#*****************************************************************
#进行复制
#*****************************************************************
weight.limit = data.frame(last(pric
obj = portfoli(data$prices,
periodicity = 'months', lookback.len = 12, silent=T,
const.ub = weight.limit,urns,1) + colSums(last(hist.returns,3)) +
colSums(last(hist.returns,6)) + colSums(last(hist.returns,12))) / 22
ia
},
min.risk.fns = list(
)
另一个想法是使用Pierre Chretien的平均输入假设
#*****************************************************************
# 让我们使用Pierre的平均输入假设
#*****************************************************************
obj = portfolio(data$prices,
periodicity = 'months', lookback.len = 12, si
create.ia.fn = create.(c(1,3,6,12), 0),
min.risk.fns = list(
TRISK.AVG = target.risk.portfolio(target.r
)
最后，我们准备看一下结果
#*****************************************************************
#进行回测
#*****************************************************************
plotb(models, plotX = T, log = 'y', Left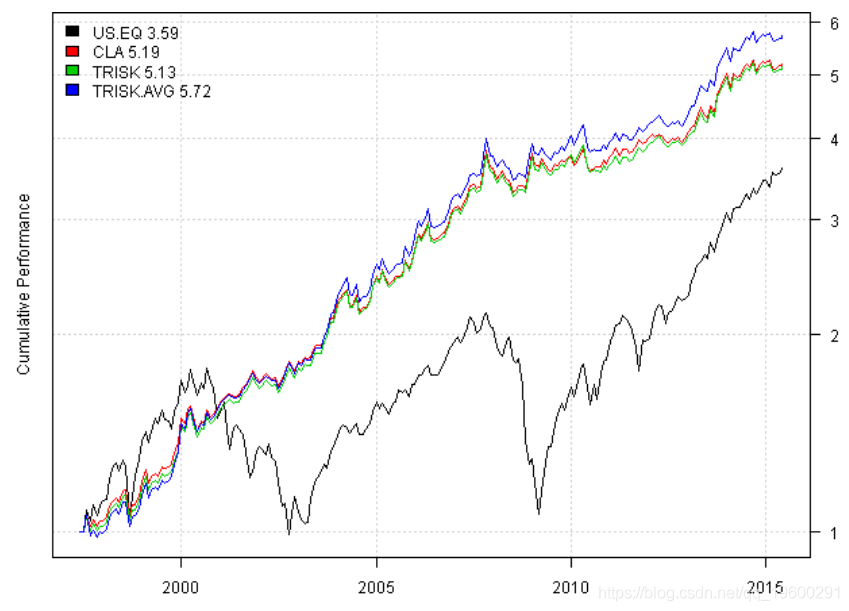
layout(1)
barplot(sapply(models, turnover, data) 随时关注您喜欢的主题
使用平均输入假设会产生更好的结果。我想应该注意的主要观点是：避免盲目使用优化。相反，您应该使解决方案更具有稳健性。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
Python深度强化学习对冲策略：衍生品投资组合套期保值Black-Scholes、Heston模型分析
R语言马科维茨Markowitz均值-方差(风险投资模型)分析最优投资组合数据预期收益率可视化
【视频】因子分析简介及R语言应用实例：对地区经济研究分析重庆市经济指标
R语言宏观经济学：IS-LM曲线可视化货币市场均衡
