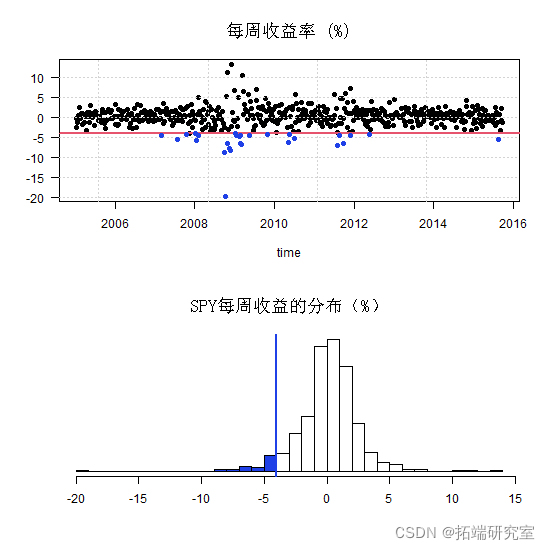
什么是尾部相关性？假设市场出现了属于最差 5% 的日子的回撤：
有人可以问，鉴于市场处于蓝色区域，特定股票下跌的概率是多少？
第一，许多学者认为沪深两市的收益率之间存在很强的相关性。董彬彬(2010) [1] 研究证明，上证综指和深证成指之间具有高度的相关性。刘喜波、王增、谷艳华(2015) [2] 研究表明，沪深股市日收益率序列之间呈现出很高的相关性，表现为当沪深两市出现大幅震荡时，两市收益率的协同作用就会大幅增强。陈梦龙(2016) [3] 研究表明，沪深两市收益率之间存在较高的正向动态条件相关关系，且具有较强的持续性和平稳性。卢俊香、武宇、杜艳丽(2016) [4] 研究发现，沪深股市日收益率序列呈现出较强的相关性以及对称的尾部相关性，当沪深两市出现大幅震荡时，两市收益率的协同作用将大幅增强。
第二，许多学者认为沪深两市的收益率之间存在很强的尾部相关性。余平、钟波(2007) [5] 研究发现，上证综指和深圳成指之间所存在的尾部相关性主要表现在它们之间具有较强的Clayton Copula下尾关系。类似地，闫海梅、王波(2010) [6] 研究也认为，沪深两市股票指数之间的Clayton Copula下尾相关性很显著；毕付宽(2015) [7] 的研究也表明沪深两市在下跌时相关系数更大。吴鑫育、李心丹(2017) [8] 的研究结果表明，沪深股市交易量和价格两个变量的尾部相关性都具有明显的Clayton Copula下尾非对称特征。
第三，尽管不少学者认为中国沪深两市收益率之间存在很强的相关性和尾部依赖性，但是其长期关系并不具有协整性。吴栩、宋光辉、董艳(2014) [9] 通过对沪深股市夏普比率进行研究发现，沪深股票市场间的协整性不明显，其相关性呈现多重分形波动特征。
对于沪深股票市场价格收益指数之间的相关性问题，以上研究虽然已经得出了一些有益的结论，但是，也存在不少问题。
第一，虽然这些研究都证明上证综指与深证成指收益率之间具有较强的相关关系，但却都没有从因果关系的角度解释二者之间互相影响的方向性，对于两个市场如何互相影响缺乏逻辑解释，所以，本文将研究它们之间的双向因果关系。
第二，两个时间序列之间的依赖关系不仅可能存在长期关系，而且也可能存在短期关系，多数研究对于长期关系关注较多，却对于短期关系研究较少，所以，本文将从长期和短期两个方面研究沪深股市收益率指数之间的协整关系和因果关系。
第三，多数有关沪深两市股票收益率之间关系的研究，都集中在对于它们之间静态关系的研究，而对于动态关系的研究较少，所以，本文也将研究它们之间的动态相关性。
第四，以上对于沪深股市收益率尾部之间依赖关系的研究，基本都认为沪深股市收益率之间存在显著的Clayton Copula下尾依赖，但不存在显著的Gumbel Copula上尾依赖。
参考文献 (References)
-
1. 董彬彬. 中国沪深股市相关性研究[J]. 市场周刊: 理论研究, 2010(1): 61-63.
-
2. 刘喜波, 王增, 谷艳华. 基于Copula模型的沪深股市日收益率的相关性研究[J]. 数学的实践与认识, 2015, 45 (11): 101-108.
-
3. 陈梦龙. 中国股票市场的非对称相关性——基于AG-DCC-MGARCH模型的实证分析[J]. 区域金融研究, 2016 (9): 41-48.
-
4. 卢俊香, 武宇, 杜艳丽. 基于Copula的沪深股市相依结构与相关模式研究[J]. 四川理工学院学报(自然科学版), 2016, 29(2): 70-74.
-
5. 余平, 钟波. 基于Copula函数的沪深股市相关性研究[J]. 山西师范大学学报(自然科学版), 2007, 21(3): 28-32.
-
6. 闫海梅, 王波. 沪深300指数与沪深股市尾部相关性分析[J]. 数学的实践与认识, 2010, 40(22): 50-55.
-
7. 毕付宽. 基于非参数核密度估计时变相关Copula的沪深股市相关性研究[J]. 时代金融, 2015(10): 25-32.
-
8. 吴鑫育, 李心丹. 中国股市量价尾部相关性研究——基于随机Copula模型的实证[J]. 金融理论与实践, 2017(1): 93-97.
-
9. 吴栩, 宋光辉, 董艳. 沪深股市夏普比率的多重分形相关性分析[J]. 经济数学, 2014(2): 9-14.
-
10. Jorion, P. (2007) Value at Risk: The New Benchmark for Managing Financial Risk. McGraw-Hill, New York.
我们都了解股票相对于市场的贝塔系数、股票相对于市场的敏感性（例如标准普尔 500 指数）的概念。
尾部相关性的概念类似，因为它是股票对市场回撤的敏感性。如果每次市场下跌，股票下跌，那将意味着两件事：
1. 鉴于市场已经下跌，股票下跌的概率是 100%。
2. 股票对市场下跌非常敏感
直观地认为，这样的方法会与高beta 值相伴而行。但这并不是一对一的。很有可能的是，与另一只低beta 的股票相比，高beta 的股票对下跌的敏感度较低。
形式上，股票左尾对市场左尾的相关性定义为：
(1) 
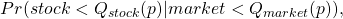
其中 Q 是分位数，这取决于您如何定义尾部，在我们的示例中为 5%。从概率来看，如果两个事件是独立的，那么看到这两个事件的概率是每个事件概率的乘积：
(2) 
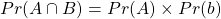
其中 A 是事件：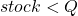 
, B 是事件 
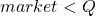。根据经验，我们所做的估计只是简单地计算位于股票 5% 临界值以下的点数，对于位于市场 5% 以下的每个点。这个函数使用这个概念来衡量两个时间序列之间的尾部相关性：
# cc参数定义了尾部。默认为5%。
co<- function{
# 如果两个序列不在同一长度上，则停止。
if(length!=length(sb)){stop }
TT <- length(# 计算有多少是低于5%的 ind0 <- ifelse ind <- which # 鉴于序列a低于5%（意味着有缩减），计算序列b中有多少个 ind1 <- sum(ifelse(reb<quantile,1,0)) # 计算概率 p0 <- id1/TT # 两者都放弃的概率
让我们拉出 10 只 ETF，看看 beta 与尾部相关性度量有何不同。我们拉动股票代码并转换为每周收益。
sym
l=length
end
dat0 = (getSymbols
n = NROW
w0 <- NULL
for (i in 1:l){
dat0 = getSymbols
w1 <- weeklyReturn
w0 <- cbind
}
现在我们计算 beta 和尾部相关性度量，并绘制它。
pr <- bet <- NULL
for(i in 1:(l-1)){
bet\[i\] <- lm
pr\[i\] <- cortr
}
barplot
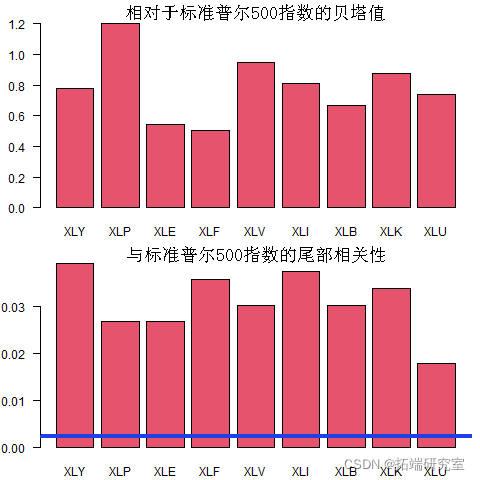
蓝线是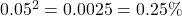 
这是我们对两个完全（尾部）独立序列的期望。
用简单的计量经济学对尾部相关性建模，可以考虑使用回归设置。使用无截距回归同样可以达到第二张图表的底部面板：
(3) 
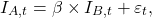
其中，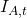 
是事件 A 发生时股票出现回撤的指标函数。看一看：
fiquan <- quantile
indl <- ifelse
betdpe <- NULL
for(i in 1:(l-1)){
fivuan <- quantile
indk <- ifelse
betence\[i\] <- lm$coef\[1\]
}
因此，我们可以使用我们对回归的了解并将分析扩展到多变量案例，而不是使用困难的多维 copula 和收敛问题。
在不仅有B的缩减，而且有C和D的缩减的情况下，我们看到A的缩减有多大可能。
不足和展望
– 我们可以进行推断，但不使用回归系数的通常 STD，因为它是指标回归.
– 我们还必须包括交互项，以使推理有效。
– 我们用更新的回归方法来改进估计；套索lasso、bagging等
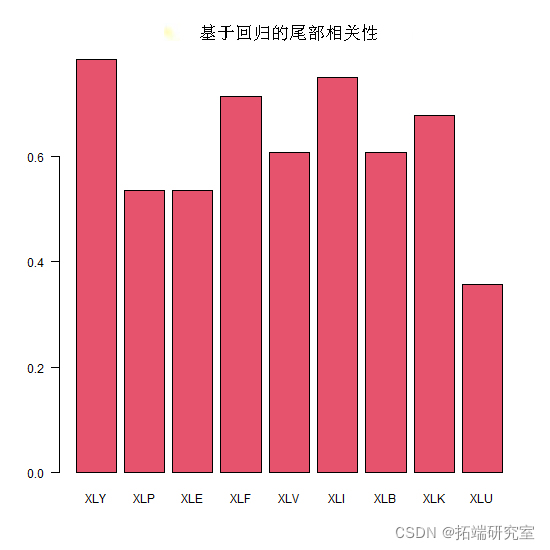
最后，我想知道 XLU（公用事业）ETF 的情况如何，为什么尾部相关性相对于 beta 而言看起来很弱，以及与 XLY（消费者自由裁量权）相比，情况有何不同。
plot lines(lowess, lwd = 2, col = 4)
我们的估计对一些极端观察很敏感。也许稳健的回归会提供更稳定的估计，因此这是另一个可能的扩展。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
文本挖掘分析多元应用：新能源汽车股市、英国封锁、疫情旅游与舆情分析
R语言Stan贝叶斯回归置信区间后验分布可视化模型检验
R语言分类回归分析考研热现象分析与考研意愿价值变现
R语言神经网络模型金融应用预测上证指数时间序列可视化
