现在，分位数回归已被确立为重要的计量经济学工具。

由Kaizong Ye，Liao Bao撰写

与均值回归（OLS）不同，目标不是给定x的均值，而是给定x的一些分位数。您可以使用它来查找具有良好上升潜力的股票。

您可能会认为这与股票的beta有关，但是beta与OLS相关，并且是对称的。

首先随机变量X的分布函数为：

$F(x)=P(X \leq x)$

则它的 $\tau$ 分位数可定义为： $Q_{\tau}(X)=arginf \left\{ x \in \mathbb{R}; F(x)\geq\tau \right\} (0<\tau<1)$

若将分布函数F（x）的逆定义为：

$F _{X}^ {-1}(\tau)=inf[y\in \mathbb{R}; F(y)\geq\tau]$

则

$Q_{\tau}(X)=F_{X}^{-1}(\tau)$

设有随机向量（X，Y），其中Y在给定X=x的情况下的条件累积分布函数为 $F_{Y|X=x}(y|x)$ ，则将该条件随机变量Y|X=x的 $\tau$ 条件分位数定义为： $Q_{\tau}(Y|X = x)=arginf \left\{ y\in \mathbb{R}:F(y|x)\geq\tau \right\} (0<\tau<1)$

假定我们有样本序列 $\left\{ (X_{i},Y_{i} ),(i=1,...,n)\right\}$ 满足下列回归模型，即

$Y=m(X)+\epsilon \quad X \in \mathbb{R}$

假定误差项 $\epsilon_{i}\left\{ i=1,...,n \right\}$ 为独立同分布的序列，且分布情况未知，这Y的 $\tau$ 条件分位数 $m_{\tau}(x)=argmin_{\theta \in \mathbb{R}}\mathbb{E}\left\{ \rho_{\tau}(Y-\theta)|X=x\right\}$

式中， $\rho_{\tau}(u)=u[\tau I(u \geq 0)-(1-\tau)I(u<0)]$ 为分位回归领域的损失函数，有些地方也称之为检验函数。 $I(·)$ 为示性函数。不包含示性函数的损失函数为

$\rho_{\tau}(x)=\left\{ \begin{aligned} \tau x ,u\geq0 \\ (\tau-1)x,u<0 \\ \end{aligned} \right.$

损失函数同样可以用下面一个公式进行表示：

$\rho_{\tau}(u)=u(\tau-I(u<0))$

则我们希望 $E\rho_{\tau}(x-\hat X)$ 尽可能的小，最好等于0，则： $E\rho_{\tau}(x-\hat X)=(\tau-1)\int_{-\infty}^{\hat X}(x-\hat X)dF(x)+\tau\int_{\hat X}^{\infty}(x-\hat X)dF(x)$

最优解为

$0=(1-\tau )\int_{-\infty}^{\hat{X}}dF(x)-\tau\int_{\hat{X}}^{\infty}dF(x)=F(\hat{ X})-\tau$

用样本经验分布函数代替F（x）则

$F(x)=\frac{\sum_{i=1}^{n}{I(X_{i}\leq x)}}{n}$

$\int \rho_{\tau}(x-\hat X)dF_{n}(x)=n^{-1}\sum_{i=1}^{n}\rho_{\tau}(x_{i}-\hat X)$

这些是分位数回归的一些基本思想，这仅仅只涉及到基本的分位数线性回归，还有较为复杂的核回归在随后的研究中再进行更新。

如果市场出现上涨，高beta股票将获得上行波动的收益，但对称地，当市场下跌时，您可能会遭受巨额亏损。

使用下图最好地理解分位数回归的用法：

可下载资源

完整程序、数据和文档（word）

最受欢迎的见解

1.用机器学习识别不断变化的股市状况—隐马尔科夫模型(HMM)的应用

2.R语言GARCH-DCC模型和DCC（MVT）建模估计

3.R语言实现 Copula 算法建模依赖性案例分析报告

4.R语言COPULAS和金融时间序列数据VaR分析

5.R语言多元COPULA GARCH 模型时间序列预测

6.用R语言实现神经网络预测股票实例

7.r语言预测波动率的实现：ARCH模型与HAR-RV模型

8.R语言如何做马尔科夫转换模型markov switching model

9.matlab使用Copula仿真优化市场风险

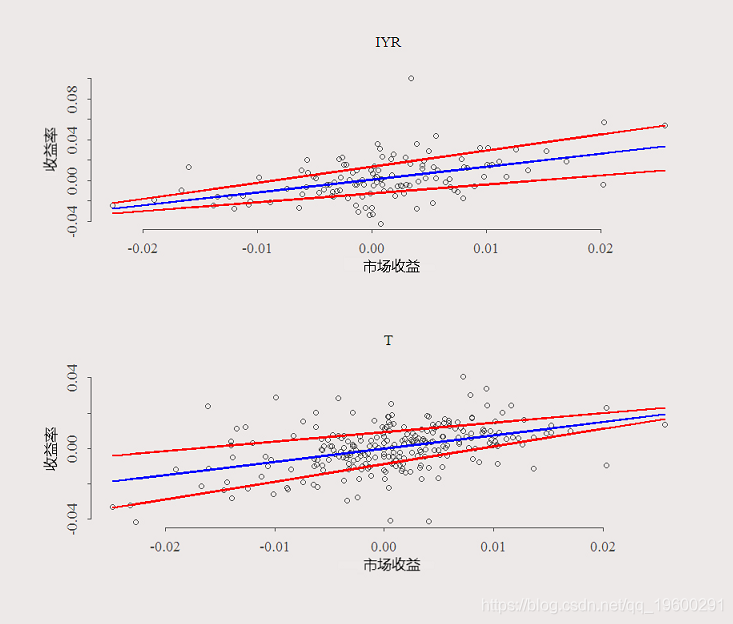
绘制的是股票收益。蓝线是OLS拟合值，红线是分位数（80％和20％）拟合值。

在上部面板中，您可以看到，当市场上涨时（X轴上的正值很高），Y轴上的分散很大。当市场下跌时，相对的分散程度而言较大。在底部面板中，情况相反。当市场上涨时，您“非常了解”股票会发生什么，但是当市场处于下跌时，股票收益的不确定性就会降低。考虑到其他因素，您希望投资组合中包含高位股票。当市场上涨时，它们收益很好，但同时在下跌的过程中提供相对的确定性。

以下代码读取股票行情，并找到最佳比率，即：上行时分散度高，而下行时分散度低：

课程

R语言数据分析挖掘必知必会

从数据获取和清理开始，有目的的进行探索性分析与可视化。让数据从生涩的资料，摇身成为有温度的故事。

立即参加 ➜


dat0 = getSymbols(sy[1], src="yahoo", from=start, to=end, 
 auto.assign = F, warnings = FALSE,symbol.lookup = F)

#查询最近365天：
dat <- gtint(sym = c(tickers,"SPY"),365) 
# 将样品划分成两部分


ins <- n/2
# 在0.2和0.8之间查找斜率 


Tau = c(.2,.8)

for (j in 1:(l-1)
for (i in 1:length(Tau)
  qslope[i,j] = rq(dat$ret[2:ins,j~dat$ret[2:ins,l, tau = Tau[i])$coef[2]

 
# 确定哪些股票有用：



dat$ret <- dat$ret[,rat0<2 & rat0>(-2)]
 
## 画图

plot(dat$ret[1:ins,which.max(rat)]~dat$ret[1:ins,l]
 
plot(dat$ret[1:n,which.min(rat)]~dat$ret[1:n,l],
title(nam)

我们使用样本的前半部分来选择我们要使用的股票。假设我们以最差的比率做空股票，并以最佳的比率做多股票。

R语言时间序列分析模型：ARIMA-ARCH / GARCH模型分析股票价格

阅读文章 ➜

dat$p <- dat$p[,rat0<2 & rat0>(-2)]
plot(dat$p[1:ins,l]/dat$p[1,l], ty = "l", ylim = c(.8,1.5),

plot(dat$p[ins:n,l]/dat$p[ins,l], ty = "l", ylim = c(.8,1.5), xlab = "样本外时期",)