
混合模型是k个分量分布的混合,它们共同形成混合分布
为什么要使用混合模型?
可下载资源
F(x )= Σk = 1ķαķFķ(x )f(x)=∑k=1Kαkfk(x)
让我们通过一个例子激发您为何使用混合模型的原因。让我们说有人向您展示了以下密度图:
高斯混合模型(Gaussian Mixture Model,简称GMM)是在高斯分布的基础上逐渐发展起来的一种聚类算法,高斯分布即为正态分布,是最为常见的数据分布形式。
假设混合高斯模型由k个高斯模型组成,则高斯混合密度函数表达式如下
(1)
其中 、 、 、 、D分别表示第k个高斯模型的概率密度函数、权重、期望、协方差矩阵和维度,从高斯混合密度函数公式可以看出,高斯混合模型就是从多个高斯分布中生成的数据模型,即无论是什么形状的分布,只要高斯函数的数量足够多,大量的高斯函数进行线性组合,就可以准确地表示出任意形状的分布,即构建出任意的高斯混合模型,随着高斯函数数量的增加,这个高斯混合模型就会变得足够复杂,就可以用来逼近任意连续的概率密度分布,正是由于高斯混合模型能够近似地模拟任意形状函数的密度分布,高斯函数的计算性能良好,并且其结果准确可靠,因此近年来高斯混合模型在生物识别中得到广泛的应用。
p <- ggplot(faithful, aes(x = waiting)) +
geom_density()
p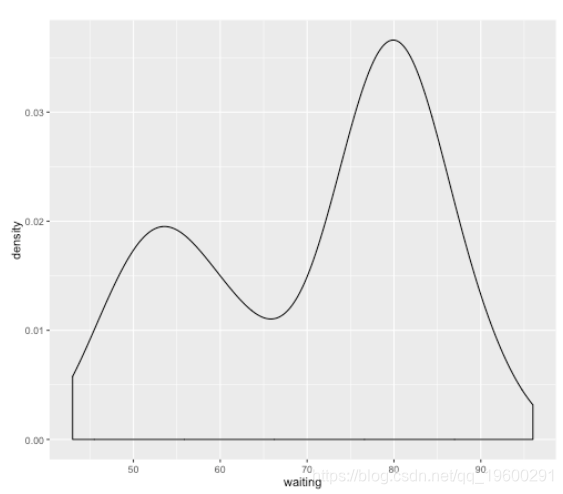
我们可以立即看到所得到的分布似乎是双峰的(即有两个凸起),表明这些数据可能来自两个不同的来源。
head(faithful)
## eruptions waiting
## 1 3.600 79
## 2 1.800 54
## 3 3.333 74
## 4 2.283 62
## 5 4.533 85
## 6 2.883 55 该数据是2列data.frame
- 火山喷发:喷发时间(分钟)
- 等待:喷发之间的时间(分钟)
p +
geom_vline(xintercept = 53, col = "red", size = 2) +
geom_vline(xintercept = 80, col = "blue", size = 2)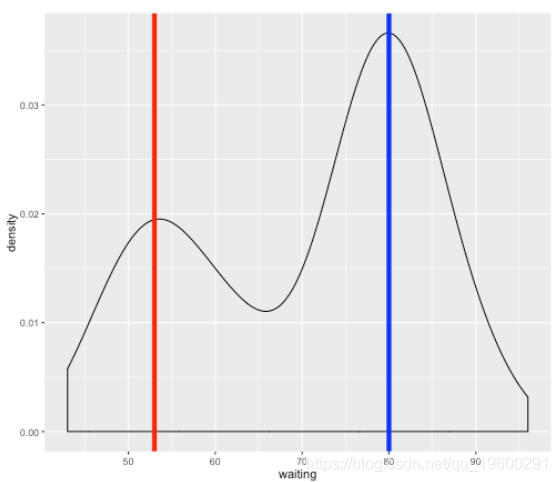
使用高斯混合模型进行聚类
执行混合模型聚类时,您需要做的第一件事是确定要用于组件的统计分布类型。
正态分布由两个变量参数化:
- μμ
- σ2σ2
我们将用 代码来演示GMM的实际应用:
set.seed(1)
wait <- faithful$waiting
mixmdl <- normalmixEM(wait, k = 2)data.frame(x = mixmdl$x) %>%
ggplot() +
fill = "white") +
stat_function(geom = "line", fun = plot_mix_comps,
args = list(mixmdl$mu[1], mixmdl$sigma[1], lam = mixmdl$lambda[1]),
(geom = "line", fun = plot_mix_comps,
args = list(mixmdl$mu[2], mixmdl$sigma[2], lam = mixmdl$lambda[2]),
colour = "blue", lwd = 1.5) +
ylab("Density")
实际上很简单; 红色和蓝色线仅表示2种不同的拟合高斯分布。平均值分别为:
mixmdl$mu
## [1] 54.61489 80.09109
分别具有以下标准偏差:
mixmdl$sigma
## [1] 5.871244 5.867716
mixmdl$lambda
## [1] 0.3608869 0.6391131

另一个重要方面是每个输入数据点实际上被分配了属于这些组件之一的后验概率。我们可以使用以下代码检索这些数据:
post.df <- as.data.frame(cbind(x = mixmdl$x, mixmdl$posterior))
head(post.df, 10) ### x comp.1 comp.2
## 1 79 0.0001030875283 0.999896912472
## 2 54 0.9999093397312 0.000090660269
## 3 74 0.0041357268361 0.995864273164
## 4 62 0.9673819082244 0.032618091776
## 5 85 0.0000012235720 0.999998776428
## 6 55 0.9998100114503 0.000189988550
## 7 88 0.0000001333596 0.999999866640
## 8 85 0.0000012235720 0.999998776428
## 9 51 0.9999901530788 0.000009846921
## 10 85 0.0000012235720 0.999998776428
x列表示数据的值,而comp.1和comp.2分别表示属于任一组件的后验概率。
最终用户决定使用什么“阈值”将数据分配到组中。例如,可以使用0.3作为后阈值来将数据分配给comp.1并获得以下标签分布。
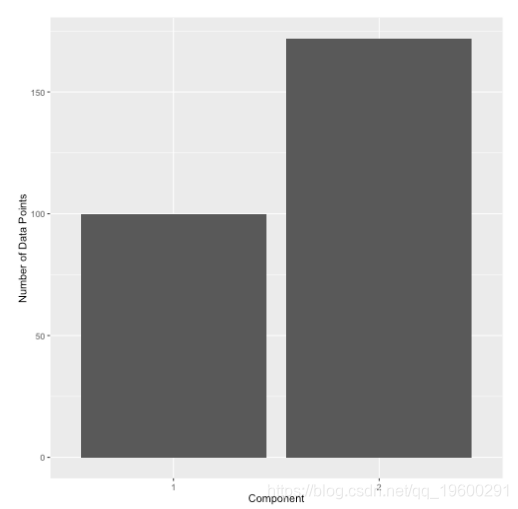
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!

 LLM与词袋、TF-IDF在新闻数据集上分类与聚类多维对比 | 附代码数据
LLM与词袋、TF-IDF在新闻数据集上分类与聚类多维对比 | 附代码数据 R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据
R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据 LLM嵌入K-Means、DBSCAN聚类、PCA主成分分析新闻文本聚类研究|附代码数据
LLM嵌入K-Means、DBSCAN聚类、PCA主成分分析新闻文本聚类研究|附代码数据 R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据
R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据



