每个动态现象都可以用一个潜过程(Λ(t))来表征,这个潜过程在连续的时间t中演化。
有时,这个潜过程是通过几个标志来衡量的,因此潜过程是它们的共同因素。
多元标记的潜过程混合模型
Proust-Lima 等人引入了潜在过程混合模型。(2006 – A Nonlinear Model with Latent Process for Cognitive Evolution Using Multivariate Longitudinal Data – Proust – 2006 – Biometrics – Wiley Online Library 和 2013 – Analysis of multivariate mixed longitudinal data: A flexible latent process approach – Proust‐Lima – 2013 – British Journal of Mathematical and Statistical Psychology – Wiley Online Library ).
使用线性混合模型根据时间对定义为潜过程的感兴趣量进行建模:
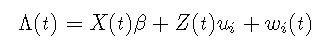
其中:
- X(t) 和 Z(t) 是协变量的向量(Z(t) 包含在 X(t) 中;
- β是固定效应(即总体平均效应);
- ui 是随机效应(即个体效应);它们根据具有协方差矩阵 B 的零均值多元正态分布进行分布;
- (wi(t)) 是一个高斯过程。
根据时间和协变量的 Λ(t) 结构模型与单变量情况完全相同。
现在,我们不再定义一个观察方程,而是定义 K 个不同标记的 K 个观察方程,其中 Yijk是对主体 i、标记 k 和场合 j 的观察。在单变量情况下,可以通过定义特定于标记的链接函数 Hk 来处理几种类型的标记。特定于标记的观察方程还可能包括协变量上的一些对比 γk 以及标记和主体特定的随机截距:
背景和定义
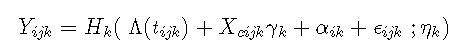
其中:
- αik~N(0,σ2k)
- Xcijk协变量向量
- γk 是对比(k 上的总和等于 0)
- tijk 对象 i、标记 k 和场合 j 的测量时间;
- ϵijk一个独立的高斯误差,均值为 0,方差为 σ2ϵkσϵk2;
- Hk将潜过程转换为标记 k 的尺度和度量的链接函数(由 ηk 参数化)。
目前只考虑连续链接函数。这些与单变量情况(在 lcmm 中)相同。H−1 是一组递增单调函数的参数族:
- 线性变换:这简化为线性混合模型(2 个参数)
- Beta 累积分布族重新调整(4 个参数)
- 具有 m 个节点的二次 I 样条的基(m+2 个参数)
可识别性
与任何潜在变量模型一样,必须定义潜在变量的度量。这里第一个随机效应 ui的方差设置为 1,平均截距(在 β 中)设置为 0。
认知过程示例
在这个例子中,当认知被定义为三种心理测试的共同因素时,我们研究了认知随时间变化的轨迹:MMSE、BVRT和IST。这里的时间尺度是进入队列后的年数,轨迹被假定为时间上的二次方(在个人和人群层面),模型被调整为进入时的年龄。为了进一步研究性别的影响,包括对共同因素的平均效应和对每个标志的差异效应(对比)(在这个例子中不与时间相互作用)。
模型考虑:
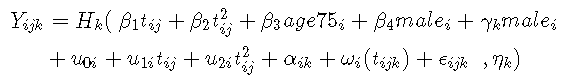
其中:
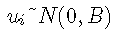 和
和 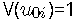 ,
, 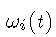 是布朗过程,
是布朗过程, 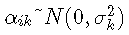 对于 k = 1,2,3:
对于 k = 1,2,3: 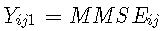 ,
, 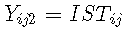 和
和 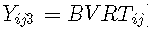
不同链接函数的估计
我们首先创建变量标准化, 避免数值问题:
tie <- (ae - ag_it)/10 ag75 <- (ae_it - 75)/10
随时关注您喜欢的主题
线性链接函数
默认情况下,所有链接函数都设置为线性:
mlmm( ubc'ID', dt = pud, radom = T, cr =B(tme))
非线性链接函数
根据数据的性质,可能需要一些非线性链接函数。例如,这里的 MMSE 是高度偏斜的:
hist(MMSE)
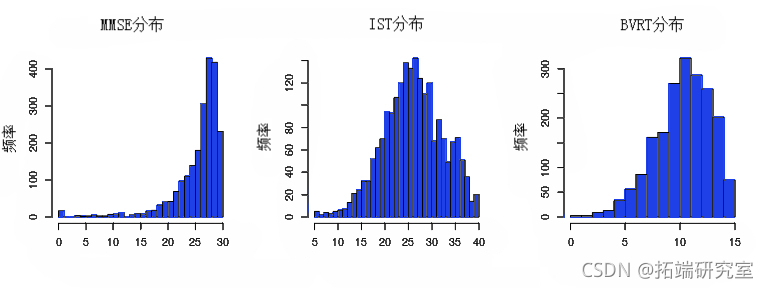
在单变量情况下,可以考虑 Beta CDF 或样条。链接函数族可以对所有标记都相同(即使参数不同):
# 以Beta为例 mlmm( lnk = 'beta')
或者可以不同地选择链接函数。例如,
请注意,样条变换有时可能涉及非常接近 0 的参数,从而导致无法收敛(因为参数位于参数空间的边界)。
# 样条曲线中不同数量的结点
mlmm( lik = c('eta','3-uan-spes','3-antpln'))
修复一些转换参数
这经常发生在 MMSE 中。例如,在下面的示例中,由于 MMSE 变换的第三个参数低于 10e-4,因此不容易达到收敛。
# 样条曲线
mlmm( axe=50, ink = c('3asin'))
通过使用 fix 选项修复此参数,可以轻松解决此问题。为此,可以从估计向量(此处为第 21 个参数)中识别参数的位置:
best

并且可以根据这些估计值和新固定的参数重新拟合模型:
# 样条曲线 mult(B=mp$best)
有了这个约束,模型就可以正确收敛。
模型比较
mult对象是多元潜在过程混合模型,它们假设潜过程的轨迹完全相同,但链接函数不同。在单变量情况下,可以使用信息标准来比较模型。该 summary 给我们这样的信息。
sumrtbe(ml)

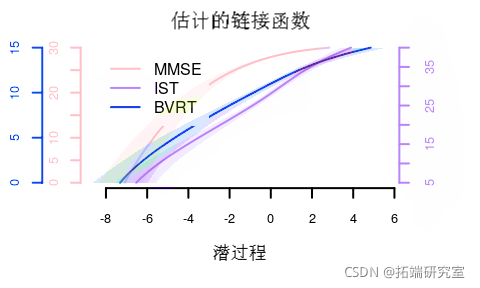
涉及 Beta 变换和样条变换的模型在 AIC 方面似乎比显示偏离正态性的线性变换要好得多。
可以在模型之间绘制和比较转换:
par(mrow=c(1,1)) plot(llnes2, col = c(ol\[2\],ol\[3\]ol4\]), ld =1,ly=4)
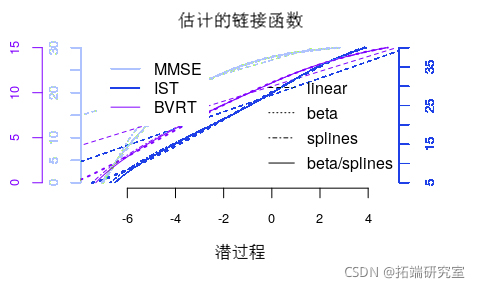
除了线性变换,所有的估计变换都非常接近。
后拟合输出
估计的链接函数:
链接函数的置信区间可以通过蒙特卡罗方法获得:
predict(ml_btapl) plt(Cl)
概括
该模型的摘要包括收敛性、拟合优度标准和估计参数。
summary






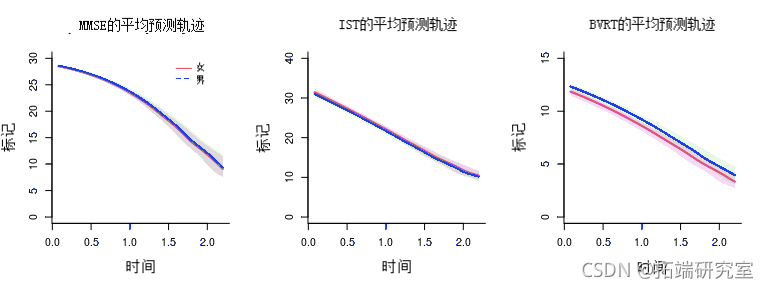
从估计结果来看,基础认知随着时间的推移有一个二次方的轨迹,基线时年龄较大的受试者的认知水平系统地较低。根据性别没有差异。然而,性别对心理测试有明显的差异性影响(P=0.0003),男性的BVRT系统性较高,女性的IST水平较高。
方差解释
对于多元数据,潜在过程是不同标记的共同潜在因素。因此,我们可以计算解释潜在过程的每个标记的残差方差。解释的这种方差取决于协变量并在特定时间计算。
VarE(tbsp,dtafme(tme=0))

例如,公因子解释了 42% 的 MMSE 残差变化,而它解释了时间 0 时 26% 的 BVRT 残差变化。
标记的预测轨迹图
可以根据协变量分布计算标记的预测轨迹,然后绘制。
predct(btapl,nwdta=dtew,va.tim='ime') plt(prec_we, ld=c(1)
拟合优度:残差图
与任何混合模型一样,我们希望特定主题的残差(右下图)是高斯分布的。
plt(mlep, 0.8)
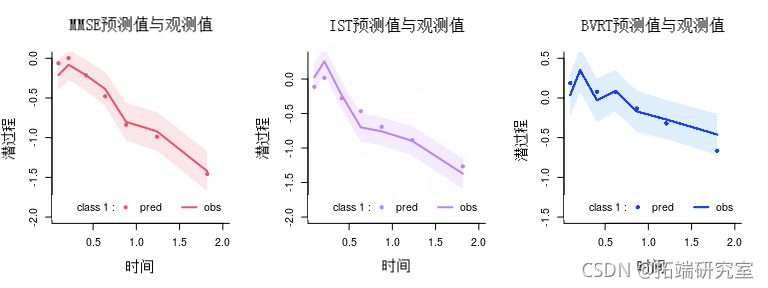
拟合优度:预测与观察的关系图
可以根据时间绘制平均预测和观察结果。请注意,预测和观察是在潜过程的范围内(观察被转换为估计的链接函数):
plot(beal, whch="fit", time="ti")

可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!

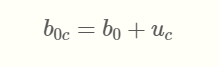
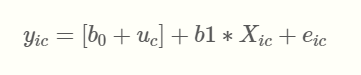
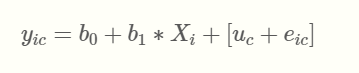

 R软件线性模型与lmer混合效应模型对生态学龙类智力测试数据层级结构应用
R软件线性模型与lmer混合效应模型对生态学龙类智力测试数据层级结构应用 R语言LCMM多维度潜在类别模型流行病学研究:LCA、MM方法分析纵向数据
R语言LCMM多维度潜在类别模型流行病学研究:LCA、MM方法分析纵向数据 Python线性混合效应回归LMER分析大鼠幼崽体重数据、假设检验可视化
Python线性混合效应回归LMER分析大鼠幼崽体重数据、假设检验可视化 R语言贝叶斯INLA空间自相关、混合效应、季节空间模型、SPDE、时空分析野生动物数据可视化
R语言贝叶斯INLA空间自相关、混合效应、季节空间模型、SPDE、时空分析野生动物数据可视化
