随着越来越多的数据被数字化，获取信息变得越来越困难。

由Kaizong Ye，Weilong Zhang撰写

我们在本文中重点关注的一个示例是评估公司面临的不同风险领域。为此，我们参考公司提交给证券交易委员会的年度报告，其中提供了公司财务业绩的全面摘要[1]，包括公司历史，组织结构，高管薪酬，股权，子公司和经审计的财务报表等信息，以及其他信息。

目的

除了通常的信息（例如股票的波动性，季节性方面）之外，公司还会发布诸如

“我们的前15名客户约占我们净销售额的80％”
“已经对我们提起产品责任诉讼”

可下载资源

完整程序、数据和文档（word）

这些作为潜在投资者对公司状况的警告[3]。目的是对公司面临的风险进行分类，这可以作为对警告投资者和潜在投资者的充分建议。

分析的意义

其中大多数是标准的东西–例如，库存波动很大，有些企业是季节性的。我们寻找异常的信息，例如“我们的前15名客户约占我们净销售额的80％”或“对我们提起了许多产品责任诉讼” – 非处方药制造商。或考虑演唱会的发起人提出：“我们承担大量债务和租赁义务，这可能会限制我们的运营并损害我们的财务状况。”

分析

根据David Blei的说法，主题模型是一种算法，用于发现大量，非结构化文档集合的主要主题。主题模型可以根据发现的主题来组织集合[2]

Topic Model

主题模型（Topic Model）是以非监督学习的方式对文档的隐含语义结构(latent semantic structure)进行聚类(clustering)的统计模型。

主题模型认为在词(word)与文档(document)之间没有直接的联系，它们应当还有一个维度将它们串联起来，主题模型将这个维度称为主题(topic)。每个文档都应该对应着一个或多个的主题，而每个主题都会有对应的词分布，通过主题，就可以得到每个文档的词分布。依据这一原理，就可以得到主题模型的一个核心公式：

$p(w_{i}|d_{j})=\sum_{k=1}^{K}p(w_{i}|t_{k})\times p(t_{k}|d_{j})$

在一个已知的数据集中，每个词和文档对应的 $p(w_{i}|d_{j})$ 都是已知的。而主题模型就是根据这个已知的信息，通过计算 $p(w_{i}|t_{k})$ 和 $p(t_{k}|d_{j})$ 的值，从而得到主题的词分布和文档的主题分布信息。而要得到这个分布信息，现在常用的方法就是LSA(LSI)和LDA。其中LSA主要是采用SVD的方法进行暴力破解，而LDA则是通过贝叶斯学派的方法对分布信息进行拟合。

LDA算法

隐含狄利克雷分布（Latent Dirichlet Allocation, LDA）是由David Blei等人在2003年提出的，该方法的理论基础是贝叶斯理论。LDA根据词的共现信息的分析，拟合出词-文档-主题的分布，进而将词、文本都映射到一个语义空间中。

LDA算法假设文档中主题的先验分布和主题中词的先验分布都服从狄利克雷分布。在贝叶斯学派看来，先验分布+数据(似然)=后验分布。我们通过对已有数据集的统计，就可以得到每篇文档中主题的多项式分布和每个主题对应词的多项式分布。然后就可以根据贝叶斯学派的方法，通过先验的狄利克雷分布和观测数据得到的多项式分布，得到一组Dirichlet-multi共轭，并据此来推断文档中主题的后验分布，也就是我们最后需要的结果。那么具体的LDA模型应当如何进行求解，其中一种主流的方法就是吉布斯采样。结合吉布斯采样的LDA模型训练过程一般如下：

随机初始化，对语料中每篇文档中的每个词w，随机地赋予一个topic编号z。
重新扫描语料库，对每个词w按照吉布斯采样公式重新采样它的topic，在语料中进行更新。
重复以上语料库的重新采样过程直到吉布斯采样收敛。
统计语料库的topic-word共现频率矩阵，该矩阵就是LDA的模型。

经过以上的步骤，就得到一个训练好的LDA模型，接下来就可以按照一定的方式针对新文档的topic进行预估，具体步骤如下：

随机初始化，对当前文档中的每个词w，随机地赋予一个topic编号z。
重新扫描当前文档，按照吉布斯采样公式，重新采样它的topic。
重复以上过程直到吉布斯采样收敛。
统计文档中的topic分布即为预估结果。

主题模型是探索或理解任何语料库集合的一种巧妙方法。首先，清理工作空间并加载所需的程序包，如下所示：

rm(list=ls()) # 清理工作空间
 
library("tm")
library("wordcloud")
library(lda)

为了简便起见，我们下载了数据，并从中提取了公司的风险部分。

textdata = readRDS("data.Rds")

我们计算词频(term frequency,TF)和逆文档频率（IDF inverse document frequency）进行评估

stpw = c("item.","1a","risk","factors","may","and","our","the","that","for","are","also","u","able","use","will","can","s")      # 选择stopwords.txt文件
stopwords('english')         # tm软件包停用词列表
comn  = unique(c(stpw, stpw1))       # 两个列表的并集
stopwords = unique(c(gsub("'","",comn),comn)) # 删除标点符号后的最终停用词lsit
 
#############################################################
#                       文本清理                     #
#############################################################
 
text.clean = function(x)                          #文本数据
{
  x  =  gsub("<.*?>", "", x)                  # 用于删除HTML标签的正则表达式
  x  =  gsub("[^[:alnum:]///' ]", " ", x)     # 仅保留字母数字
  x  =  iconv(x, "latin1", "ASCII", sub="")   # 仅保留ASCII字符
  x  =  tolower(x)                          # 转换为小写字符
  x  =  removePunctuation(x)                # 删除标点符号
  x  =  removeNumbers(x)                    # 删除数字
  x  =  stripWhitespace(x)                  # 删除空格
  x  =  gsub("^\\s+|\\s+$", "", x)          # 删除开头和结尾的空格
  x  =  gsub("'", "", x)                    # 删除撇号
  x  =  gsub("[[:cntrl:]]", " ", x)         # 用空格替换控制字符
  x  =  gsub("^[[:space:]]+", "", x)        # 删除文档开头的空白
  x  =  gsub("[[:space:]]+$", "", x)        # 删除文档末尾的空白
 
 
###########################################################
# 定义文档矩阵
###########################################################
custom.dtm  = function(x1,                               # 文本语料库
                scheme)                           # tf 或 tfidf
{
  
 
#删除空白文档（即总和为零的列）
for (i1 in 1:ncol(tdm.new)){ if (sum(tdm.new[, i1]) == 0) {a0 = c(a0, i1)} }
length(a0)    # 语料库中的空文档
if (length(a0) >0) { tdm.new1 = tdm.new[, -a0]} else {tdm.new1 = tdm.new};
 
dim(tdm.new1)    # 减少tdm
 
}

视频

文本挖掘：主题模型（LDA）及R语言实现分析游记数据

探索见解 ➜

去bilibili观看 ➜

探索更多视频 ➜

词频(term frequency,TF)定义为词t在文档d中出现的次数[7]，而逆文档频率估计整个文档集合中词的稀有性。（如果在集合的所有文档中都出现一个词，则其IDF为零。）

#tokenize以列表形式输出：
  doc.list <- strsplit(companyRDF$RF, "[[:space:
 
  # 计算词表:
  term.table <- table(unlist(doc.list))

对于我们的分析，我们使用 tf-idf， 通过较小的权重来规范出现在所有文档中的关键词的影响。

########################################################
#            创建文档矩阵           #
########################################################
 
x1 = Corpus(VectorSource(companyRDF$RF))          # 创建语料库
#x1 = n.gram(x1,"bi",2)                   # 将至少2频率的Bi-gram编码为uni-gram
 
dtm1 = custom.dtm(x1,"tf")               # 文档频率
dtm2 = custom.dtm(x1,"tfidf")            # 逆文档频率
freq1 = (sort(apply(dtm1,2,sum), decreasing =T)) # 计算词频
 
 (sort(apply(su,2,sum), decreasing =T)) # 计算词频

我们将首先在语料库中建立唯一的词汇表，然后再映射到每个公司

 
get.terms <- function(x) {
    index <- match(x, vocab)
    index <- index[!is.na(index)]

我们记录与数据集相关的统计信息。

 D <- length(documents)      #文件数 (85)
  W <- length(vocab)         # 词汇中的词数 (6662)
  doc.length <- sapply(documents, function(x) sum(x[2, ]))  # 每个文档的数量
  N <- sum(doc.length)  #数据总数

语料库中有 D = 85个文档 和 W = 6662个关键词标记。并且我们必须确定K个主题。

Topic模型为我们提供了两个主要输出：

一个是关键词概率的θ矩阵-告诉我们每个关键词属于每个主题的概率是多少。

二是ω文档矩阵-它是文档中主题比例的概率分布。

现在，我们建立了一个包含6个主题的主题模型。主题比例（α）和主题多项式的Dirichlet超参数的值分别为0.02和0.02。

最受欢迎的见解

1.探析大数据期刊文章研究热点

2.618网购数据盘点-剁手族在关注什么

3.r语言文本挖掘tf-idf主题建模，情感分析n-gram建模研究

4.python主题建模可视化lda和t-sne交互式可视化

5.疫情下的新闻数据观察

6.python主题lda建模和t-sne可视化

7.r语言中对文本数据进行主题模型topic-modeling分析

8.主题模型：数据聆听人民网留言板的那些“网事”

9.python爬虫进行web抓取lda主题语义数据分析

 
lda.cgibbs(documents = documents, K = K
                                     ,num.iterations = G, alpha = alpha
                                     ,eta = eta, initial = NU

使用LDAvis可视化拟合模型

我们已经计算了每个文档的数量以及整个语料库中关键词的出现频率。我们将它们连同θ，ω和vocab一起保存在列表中，作为数据对象 Risk，包含在LDAvis包中。

现在，我们准备调用 CreateJSON（） 函数 LDAvis。此函数将返回一个字符串，该字符串表示用于填充可视化效果的JSON对象。createJSON（）函数计算主题频率，主题间距离，并将主题投影到二维平面上以表示它们彼此之间的相似性。

  json <- createJSON(phi = RiskAnalysis$pta, 
                     doc.length = RiskAnalysis$doc.length,

serVis（）函数可以采用json并以多种方式提供结果。我们评论了以下代码，因为这是一个交互式代码。

  #serVis(json)

这是我们选择的6个主题的可视化

总体

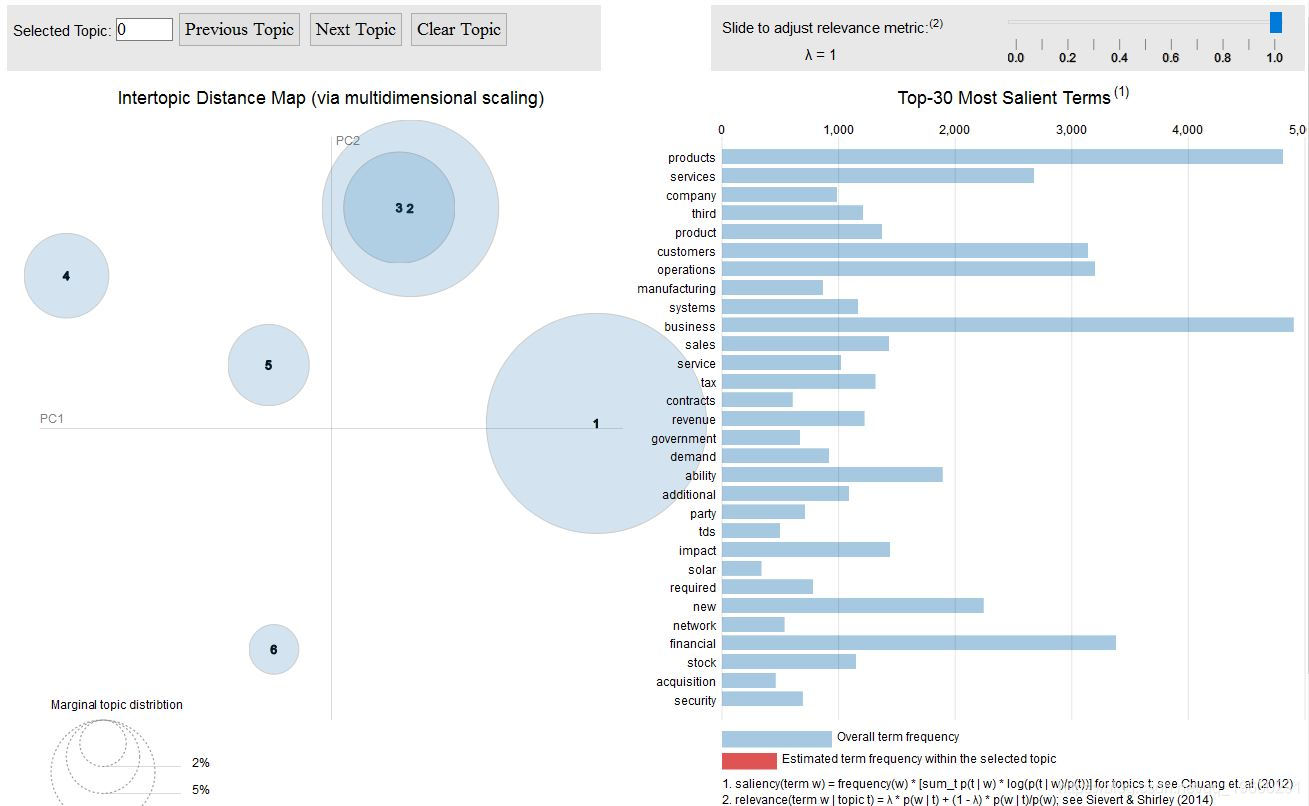
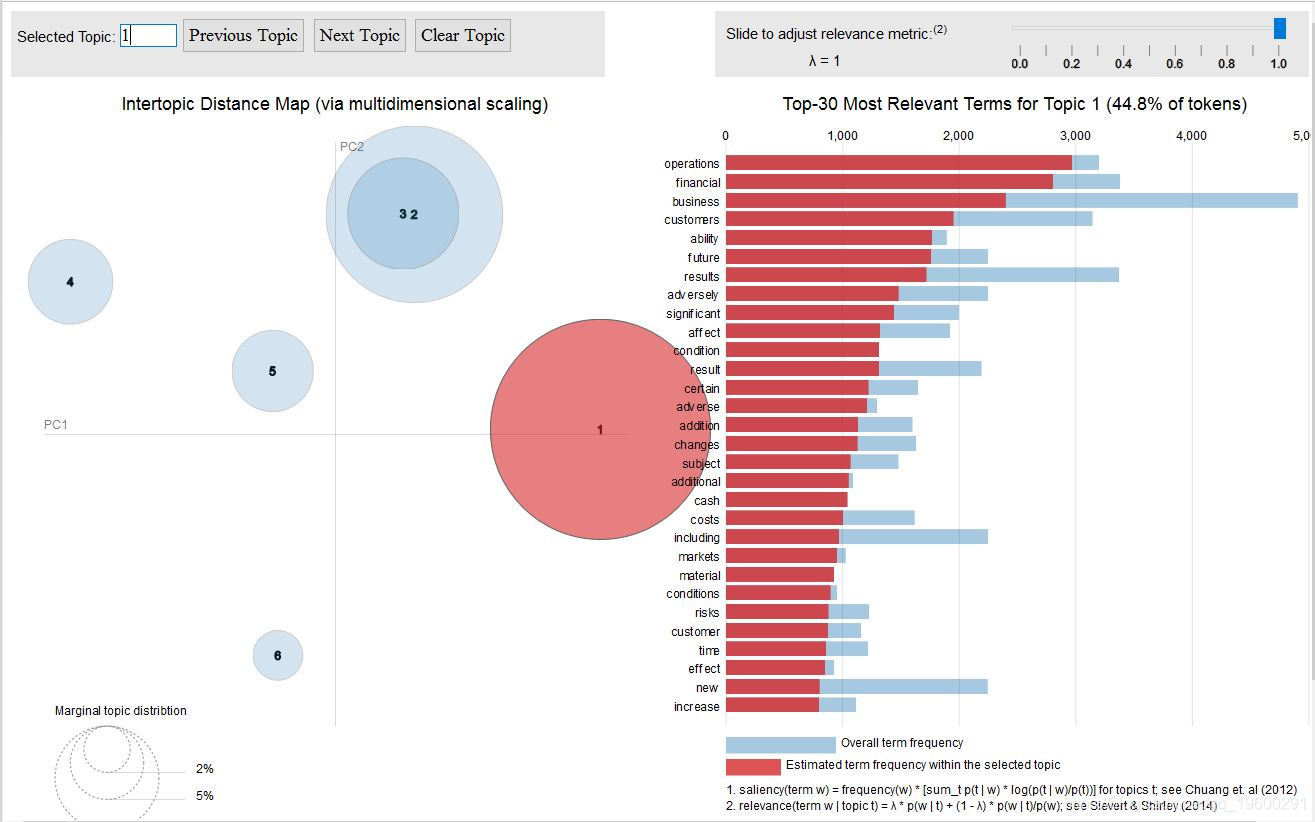
主题一

自然语言处理NLP：情感分析疫情下的新闻数据

阅读文章 ➜

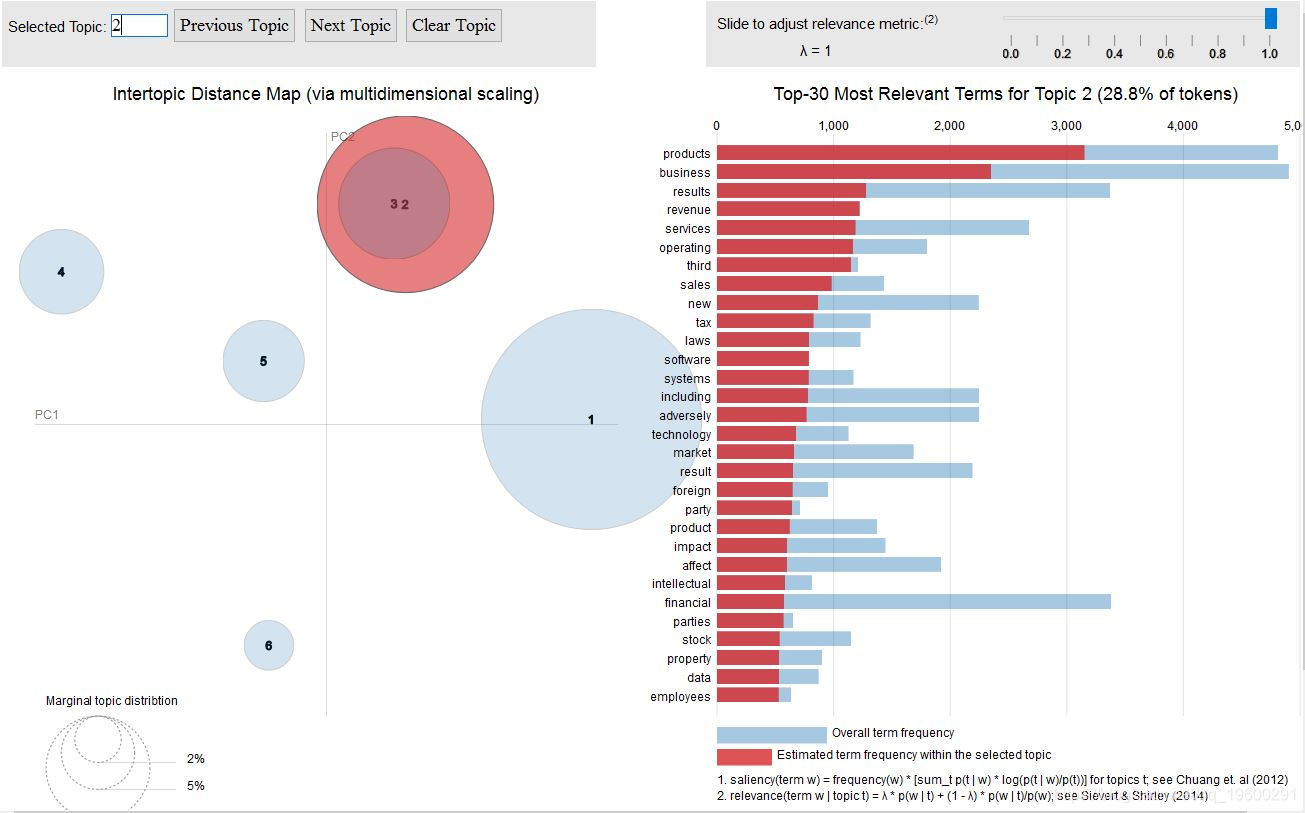
主题二

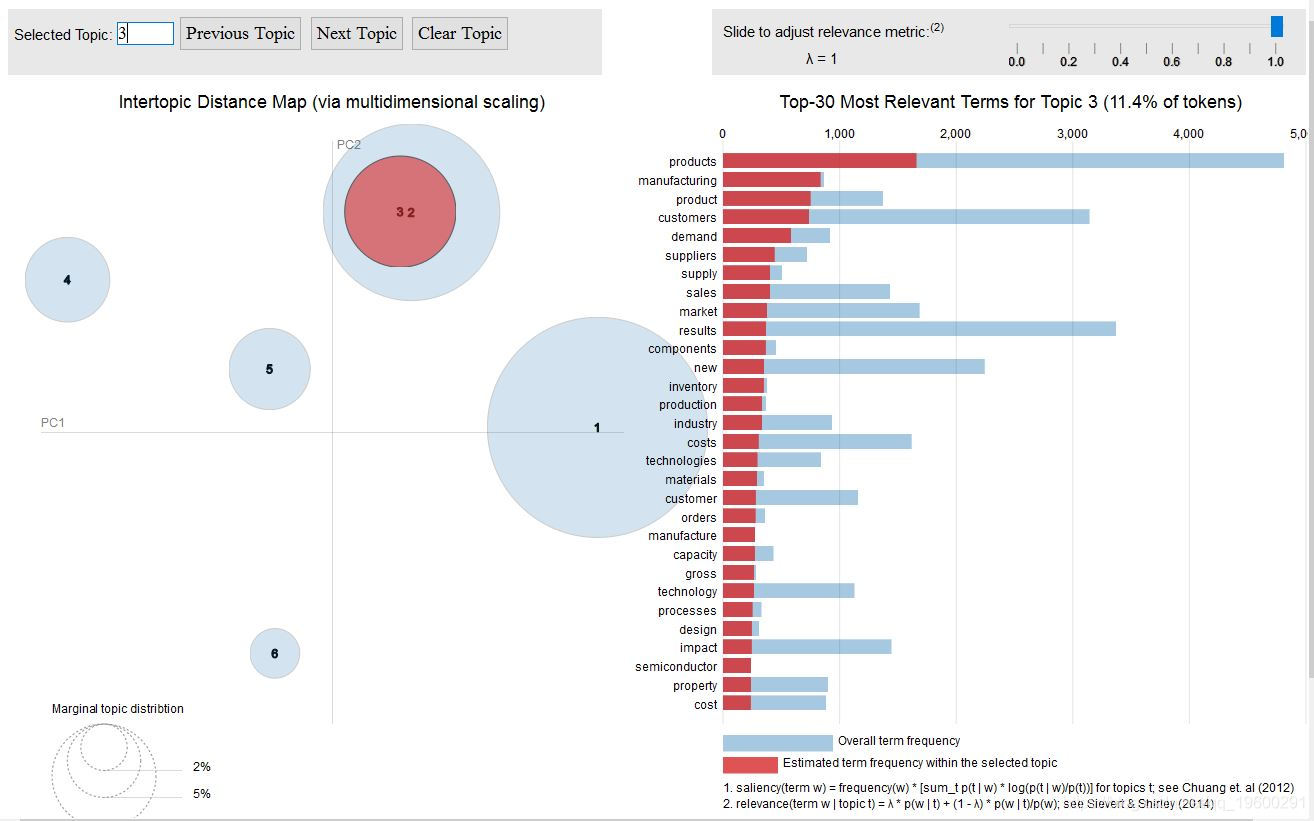
主题三

主题四

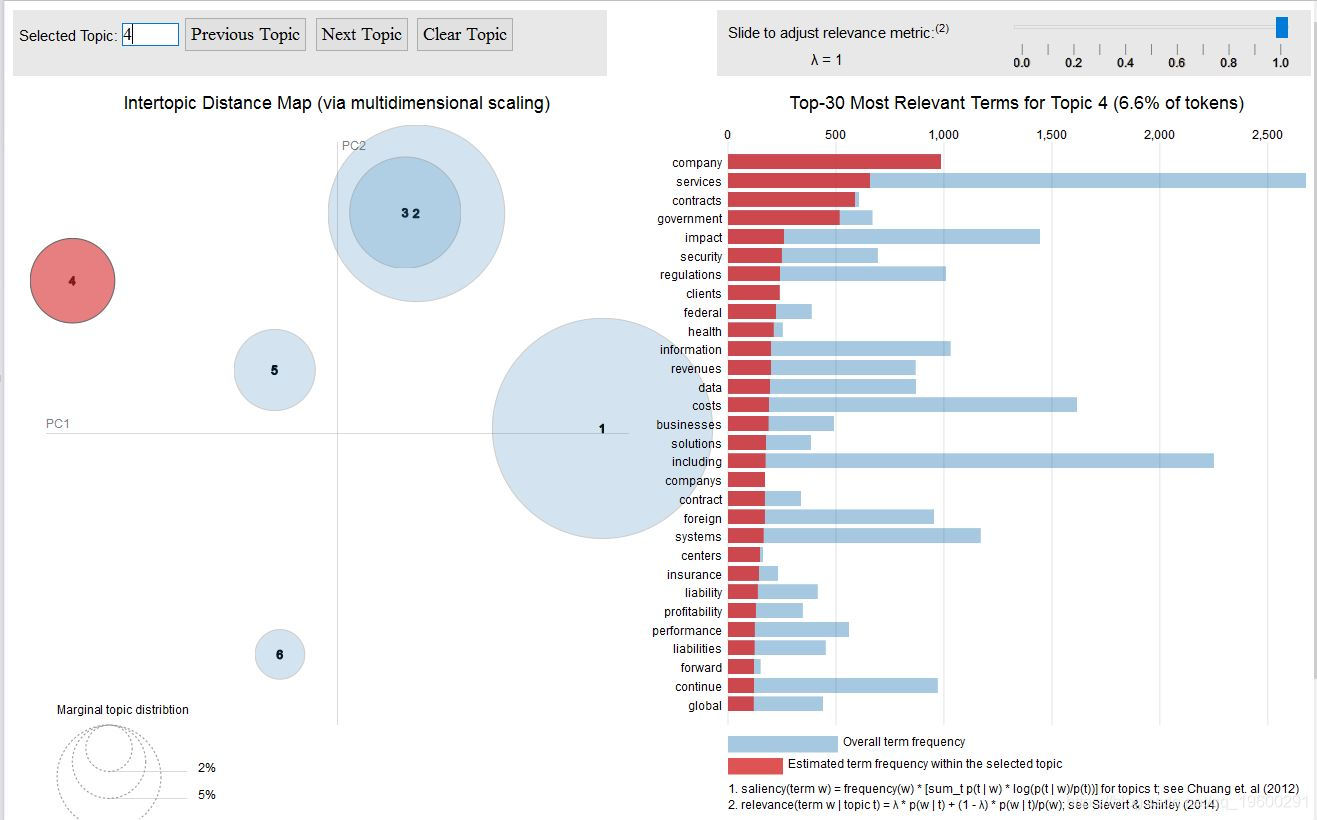
主题五

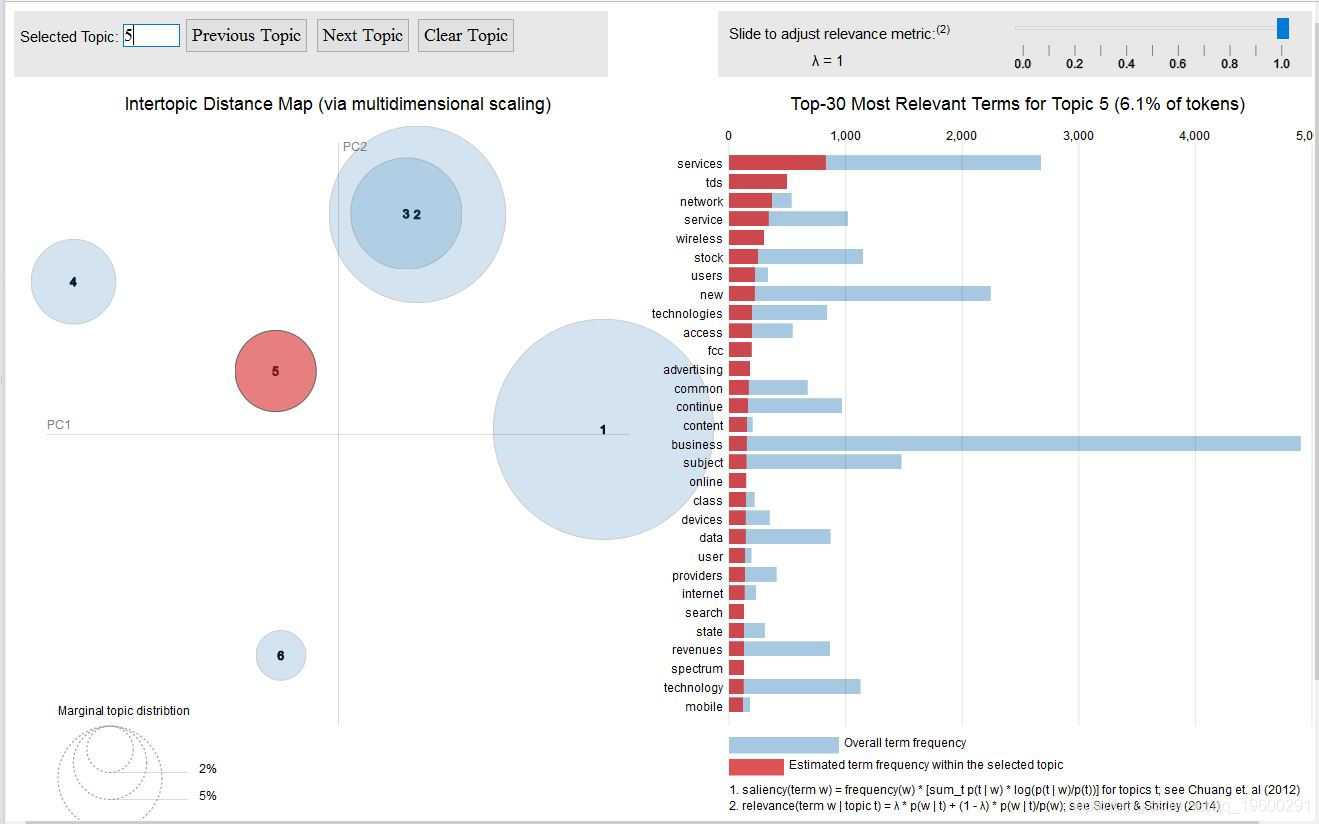
主题六

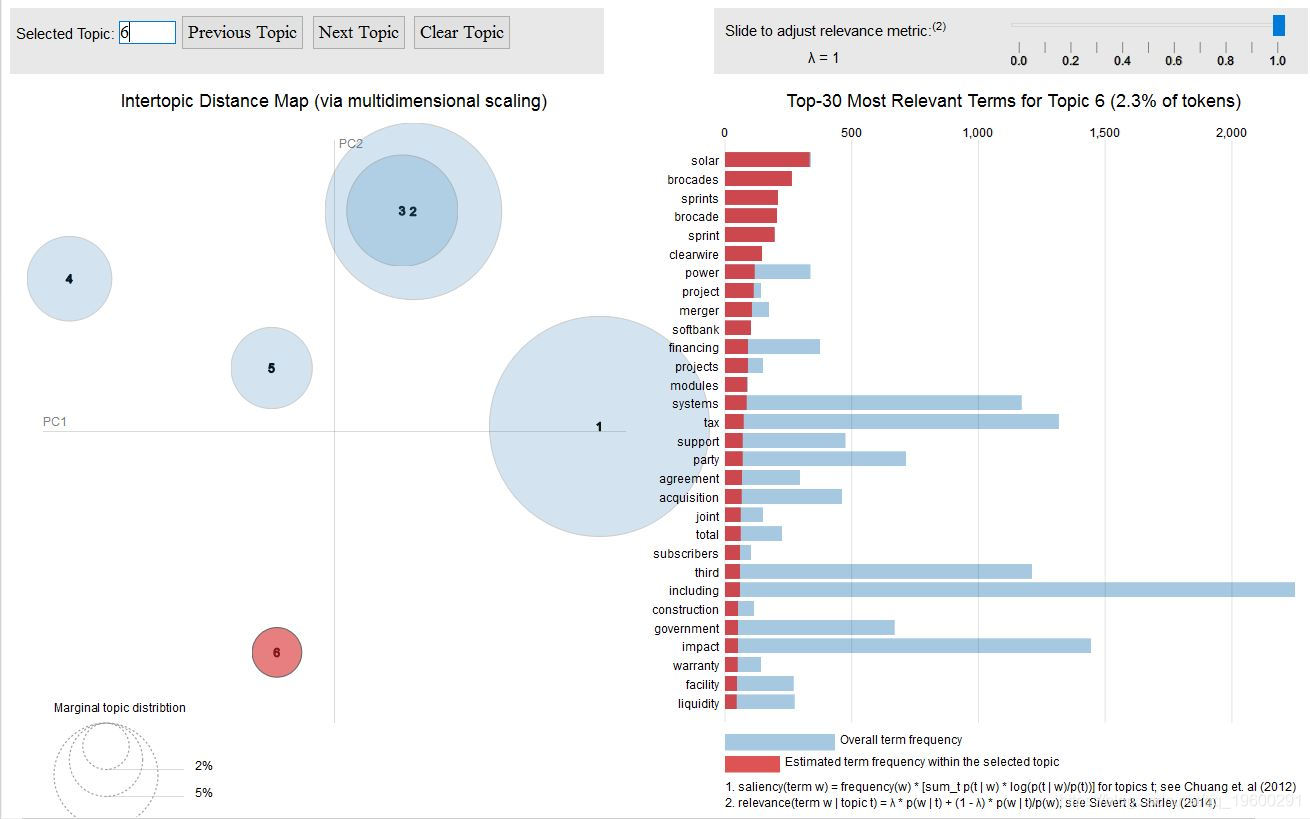
我们可以看到 Topic-2 和 Topic-3 彼此重叠，这从它们中的关键词也可以看出。但是，如果我们仔细观察一下， 主题3 则更多地涉及 制造业 ，其中涉及供应管理，需求和供应等。 主题2 则更多地涉及软件产品，运营，收入和服务。

我们选择一个值K = 6

  
K = 6 # 选择模型中的主题数
opics(dtm2,  K = K, verb = 2) # 拟合K主题模型

## 
## Top 12 phrases by topic-over-null term lift (and usage %):
## 
## [1] 'bull', 'corning', 'rsquo', 'glass', 'teledyne', 'middot', 'vpg', 'ndash', 'vishay', 'dalsa', 'dow', 'lecroy' (17) 
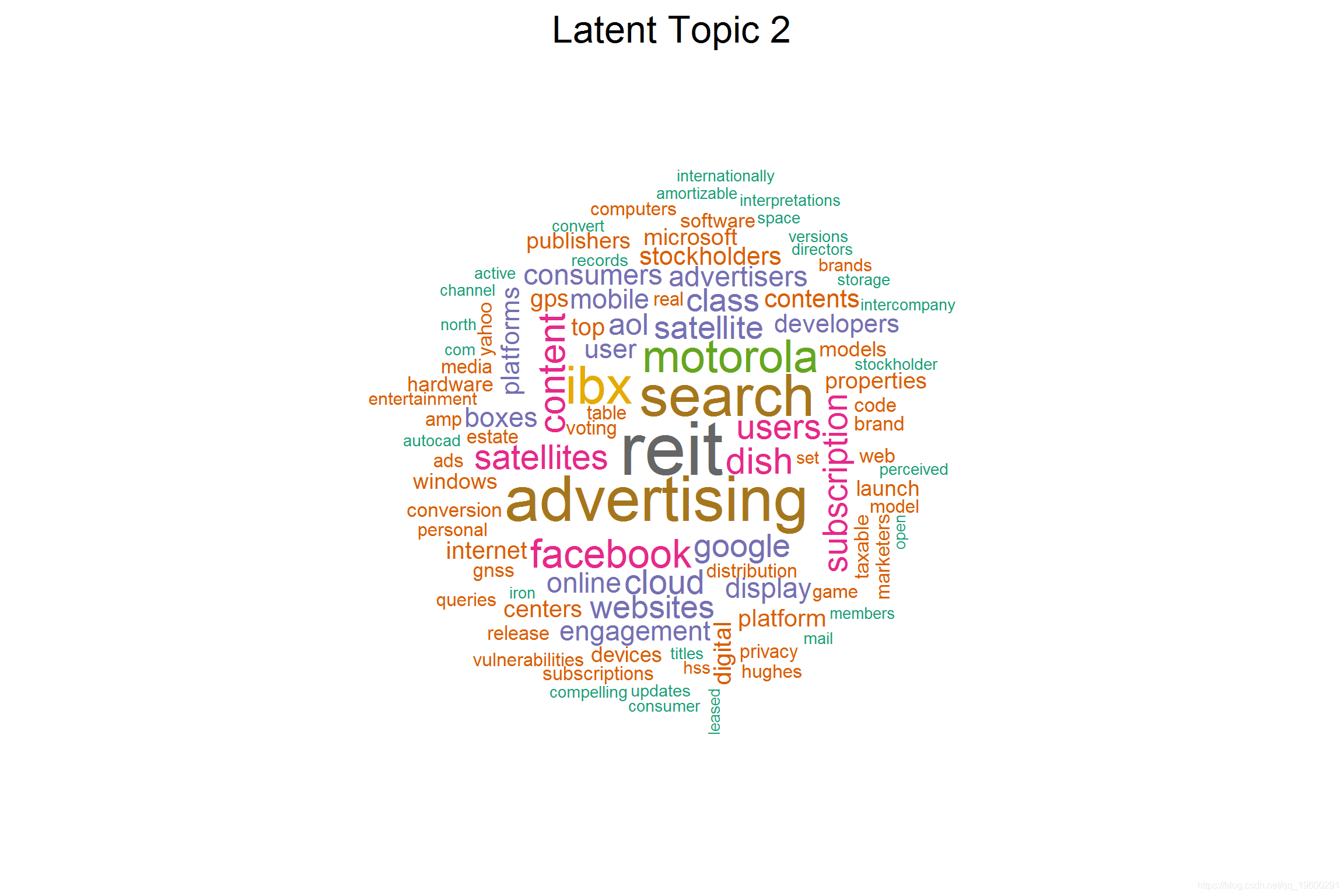
## [2] 'aol', 'advertisers', 'yahoo', 'ads', 'advertising', 'tapp', 'reit', 'apps', 'engagement', 'zuckerberg', 'ibx', 'titles' (16.9) 
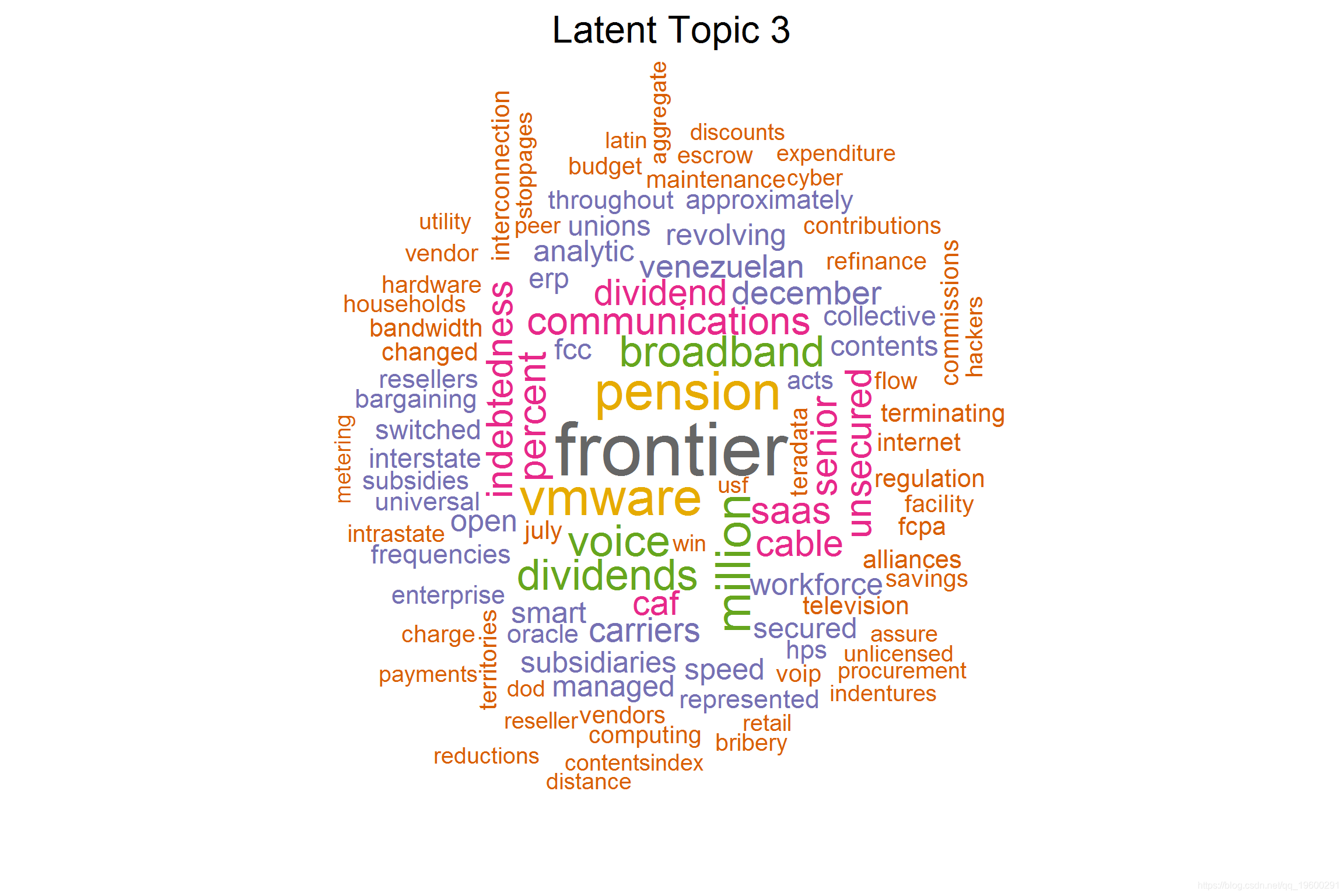
## [3] 'frontier', 'households', 'mbps', 'switched', 'escrow', 'unserved', 'windstream', 'rural', 'collective', 'territories', 'bargaining', 'tower' (16.8) 
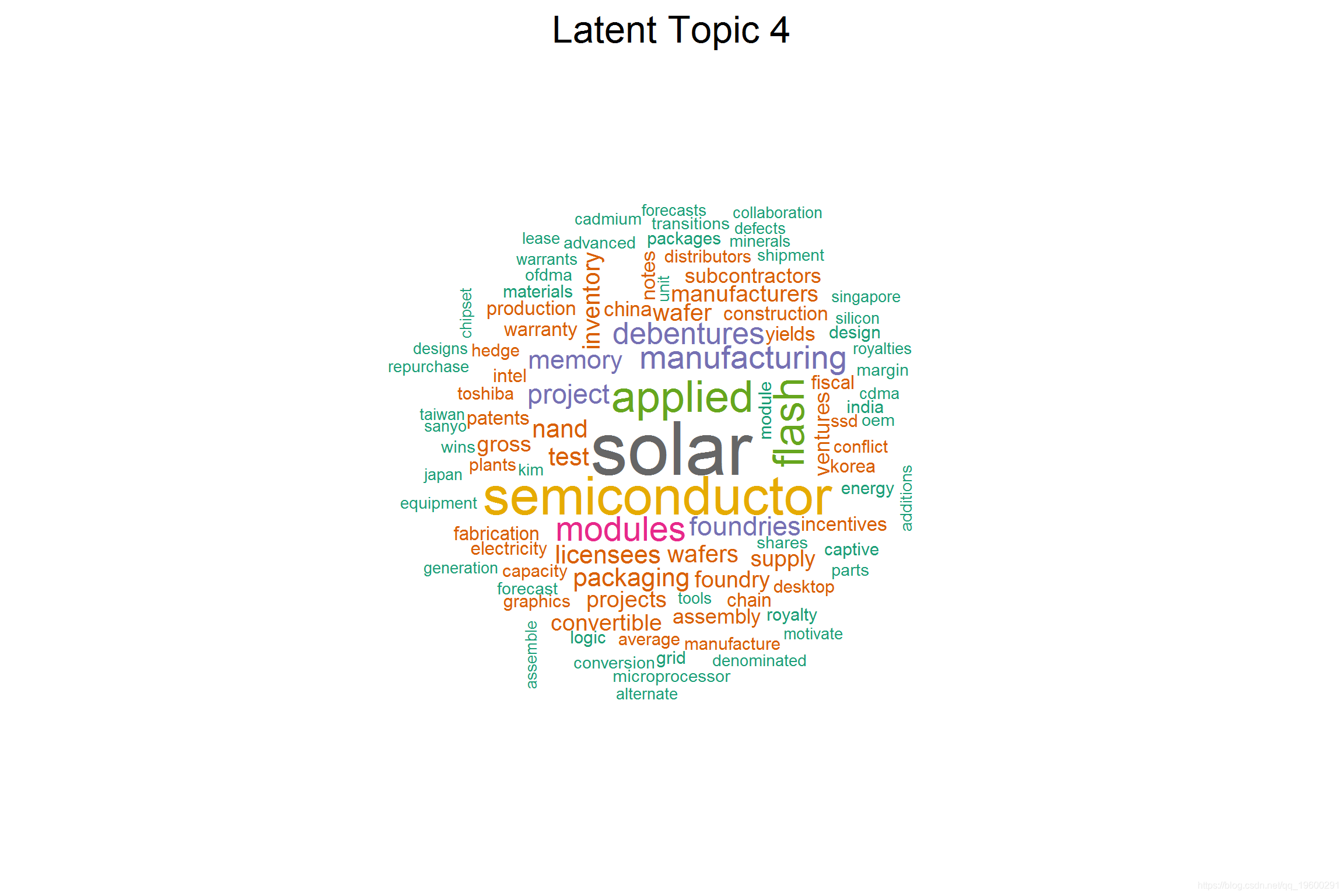
## [4] 'flash', 'nand', 'captive', 'ssd', 'solar', 'modules', 'memory', 'bics', 'reram', 'module', 'applied', 'wafers' (16.8) 
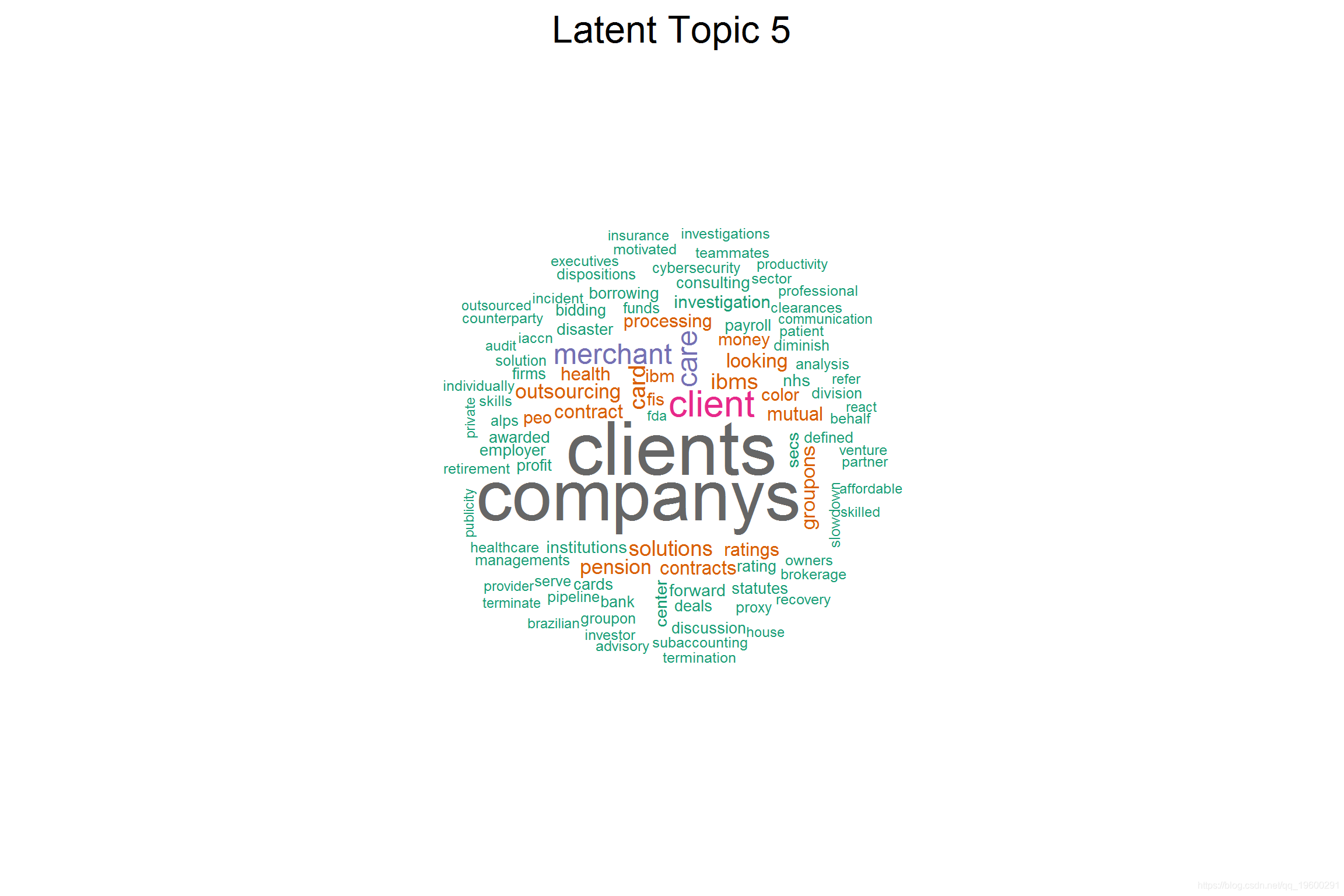
## [5] 'merchant', 'groupons', 'companys', 'peo', 'nhs', 'clients', 'iaccn', 'motivated', 'ibms', 'client', 'csc', 'lorenzo' (16.8) 
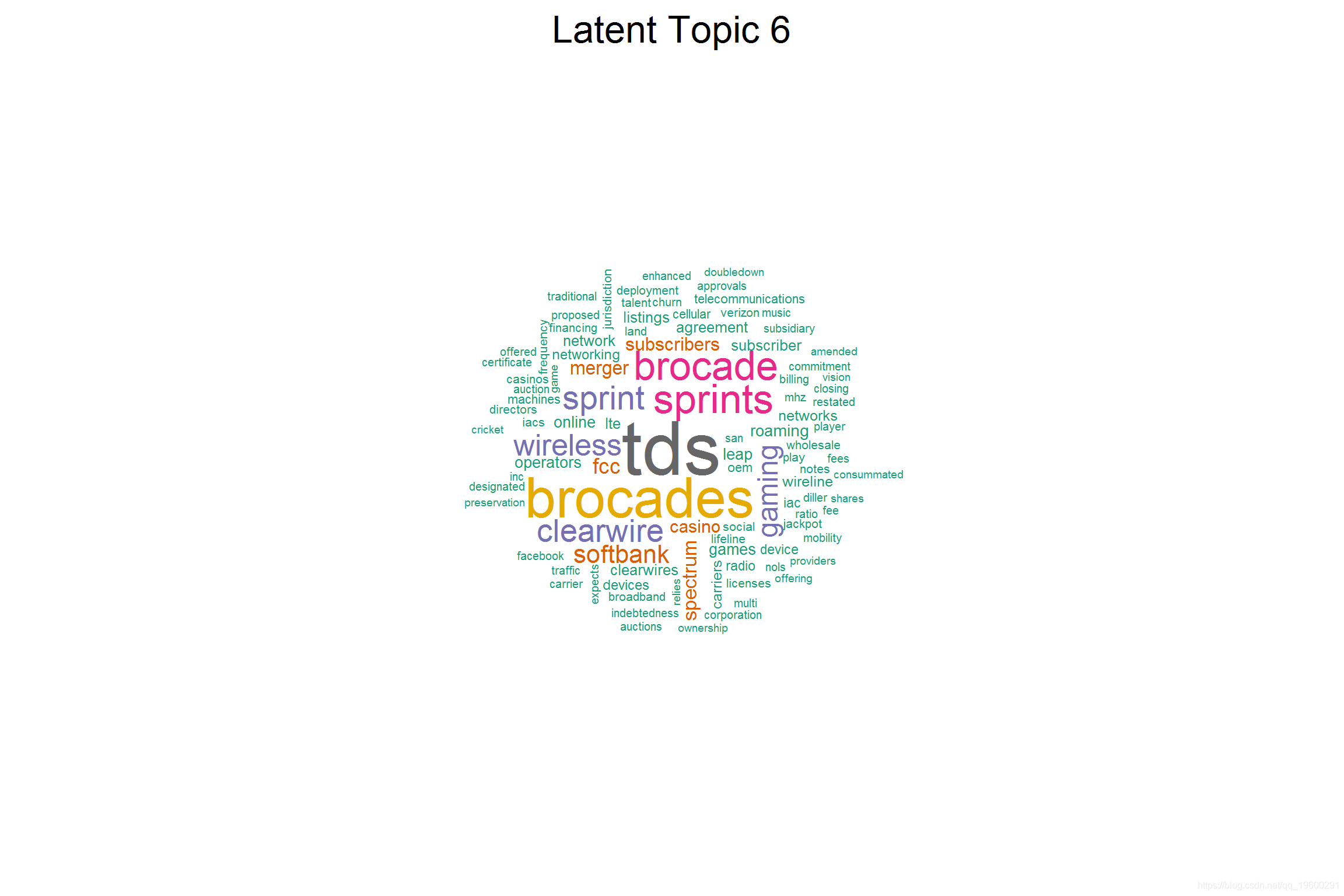
## [6] 'leap', 'cricket', 'preservation', 'blurred', 'dated', 'deploys', 'mvno', 'subsidized', 'waiting', 'rollout', 'leaps', 'dividing' (15.8) 
## 
## Dispersion = -0.01

我们来看一下项概率矩阵θ，以总项概率的降序对这个矩阵进行排序：

##            topic
## phrase                 1            2            3            4            5            6
##   tds       2.648959e-06 2.586869e-06 2.805227e-06 2.680430e-06 2.702986e-06 3.510401e-02
##   brocades  2.842265e-06 2.669269e-06 2.823106e-06 2.920408e-06 2.799614e-06 2.506861e-02
##   clients   3.646912e-06 3.546243e-06 3.928365e-06 3.578786e-06 1.898607e-02 3.969126e-06
##   companys  3.492683e-06 3.201781e-06 3.634969e-06 3.471822e-06 1.816372e-02 3.747852e-06
##   sprints   2.549403e-06 2.484293e-06 2.629347e-06 2.561769e-06 2.579702e-06 1.698829e-02
##   brocade   2.856517e-06 2.680381e-06 2.839519e-06 2.936274e-06 2.811306e-06 1.651110e-02
##   solar     3.302091e-06 3.124243e-06 3.361212e-06 1.292429e-02 3.270826e-06 3.614037e-06
##   sprint    2.578740e-06 2.513213e-06 2.669652e-06 2.595447e-06 2.609471e-06 1.278997e-02
##   reit      3.553825e-06 1.196685e-02 3.855616e-06 3.501886e-06 3.483736e-06 3.886507e-06
##   clearwire 2.549970e-06 2.484945e-06 2.630211e-06 2.562457e-06 2.580352e-06 1.193481e-02

另外，我们看到了与主题相关的文档关联概率的ω矩阵。

##         topic
## document          1          2         3          4         5         6
##       1  0.13290480 0.13105774 0.1318767 0.35729726 0.1209075 0.1259561
##       2  0.23640159 0.13706762 0.1484124 0.21041974 0.1342693 0.1334293
##       3  0.13676833 0.12301388 0.1227510 0.37290276 0.1251001 0.1194639
##       4  0.09920569 0.09944122 0.1006772 0.09860462 0.5015284 0.1005428
##       5  0.13465553 0.14035768 0.2964859 0.13016315 0.1426592 0.1556786
##       6  0.09969202 0.10480960 0.4542832 0.10026436 0.1099848 0.1309660
##       7  0.11668769 0.10861933 0.1301019 0.11348415 0.4139718 0.1171352
##       8  0.38743792 0.12338647 0.1222238 0.12780836 0.1241574 0.1149860
##       9  0.19793670 0.13959183 0.2197639 0.13766412 0.1675246 0.1375189
##       10 0.18527824 0.14644241 0.2087677 0.17083618 0.1542025 0.1344730

我们可以说文档1和文档3在主题4上的权重很大，而文档7在主题5上的权重很大。文档2是主题1和主题4的混合。

一些关键词具有高频，另一些具有低频。我们要确保词频不会过度影响主题权重。因此，我们使用称为“提升”的量度对关键词频率进行归一化。

关键词的提升是通过关键词的出现概率归一化的主题成员概率。如果某个主题的关键词提升很高，那么可以说，该关键词对于构建该主题很有用。

由于主题函数不会返回关键词的提升矩阵，因此我们可以编写一个简单的函数来计算每个关键词的提升。

 
    ptermtopic = theta[i, j]     # 关键词i是主题j成员的概率
    pterm = sum(dtm1[,i])/sum1   # 关键词i在语料库中出现的边际概率
    lift[i, j] = ptermtopic/pterm   # 因此，lift是通过出现概率归一化的主题隶属概率
      }
}

我们为以下选择的六个主题生成一个词云

 
for (i in 1:K){       # 每个主题
a0 = which(lift[,i] > 1) # 主题i的提升大于1的项
freq = theta[a0,i] # 大于1的项的Theta
freq = sort(freq,decreasing = T) # 主题i具有较高概率的关键词
 
# 自动更正提升度高于1的主题词
n = ifelse(length(freq) >= 100, 100, length(freq))
 
 
# 绘制词云图
wordcloud(rownames(top_word), top_word,  scal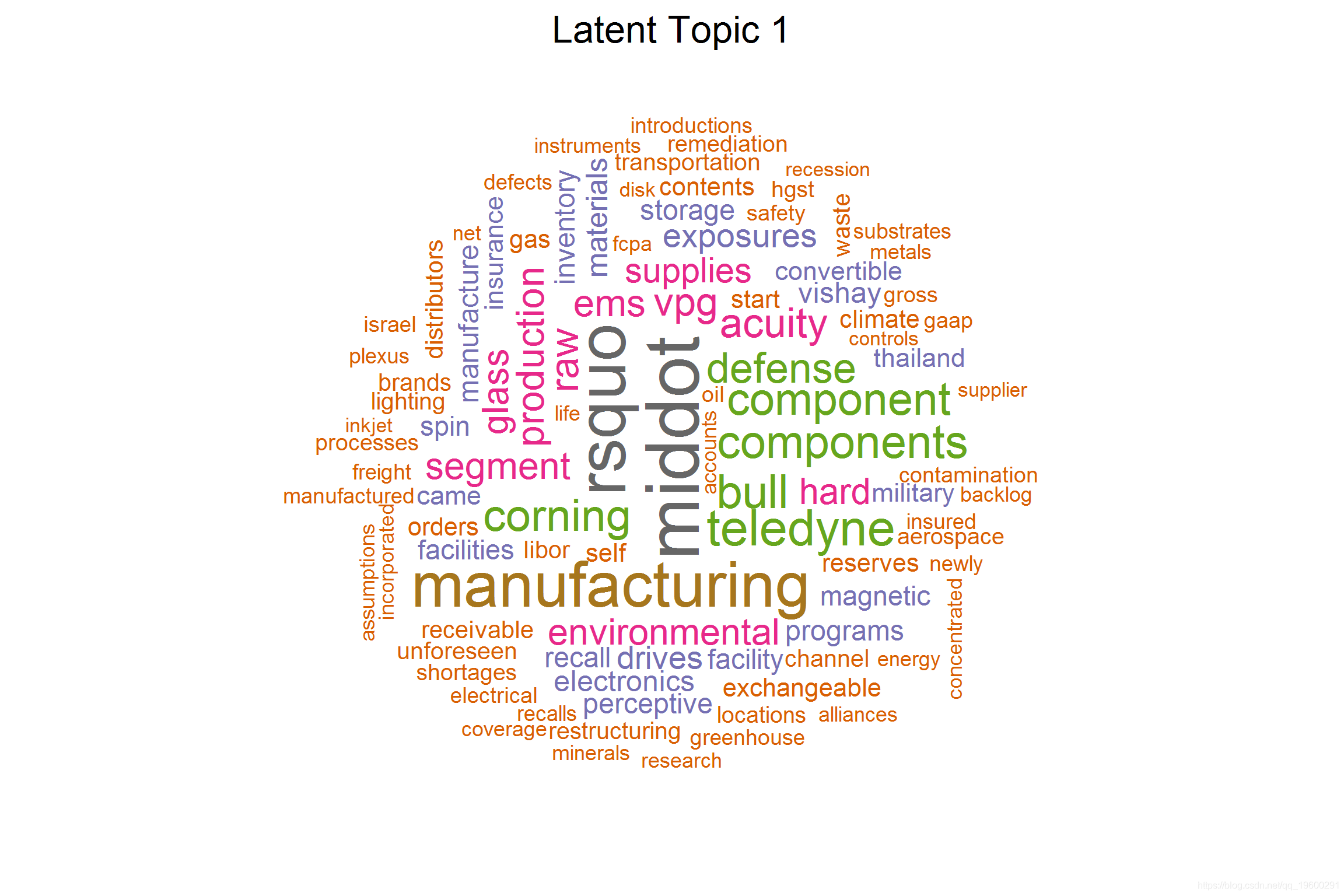

研究共现矩阵可视化图进一步了解

for (i in 1:K){       # 每个主题
a0 = which(lift[,i] > 1) # 主题i的提升力大于1的项
freq = theta[a0,i] # 大于1的项的Theta
freq = sort(freq,decreasing = T) # 主题i具有较高能力的词
 
# 自动更正大于20的词
n = ifelse(length(freq) >= 20, 20, length(freq))
 
# 现在获取前30个单词，让我们找到文档矩阵
mat  = dtm1[,match(row.names(top_word),colnames(dtm1))]
 
# 将连接数限制为2
for (p in 1:nrow(cmat)){
  vec = cmat[p, 
 
plot(graph,         #要绘制的图形
 layout=layout.fruchterman.reingold,    #布局方法 
 vertex.frame.color='blue',         #点边界的颜色
 vertex.label.color='black',        #名称标签的颜色
 vertex.label.font=1,           #名称标签的字体
 vertex.size = .00001,   # 点大小

eta = function(mat, dtm) {
 rownames(a12) = rownam 
    a13[1:15];  length(a13)
    a14a = match(a13, terms1);      # 匹配项在mat1矩阵中的位置

以下是根据我们选择的主题对公司进行的分类。

eta.file
    read_doc = mat[order(mat[,i], decreasing= T),]  # 对文档概率矩阵（twc）进行排序
    read_names = row.names(read_doc[1:n,])          # 前n个文档的文档索引
    s[[i]] = calib[as.numeric(read_names),1]     # 将前n个公司名称存储在列表中

## [1] "Companies loading heavily on topic 1 are"
## [1] "TELEDYNE TECHNOLOGIES INC"  "CORNING INC"                "VISHAY INTERTECHNOLOGY INC" "BENCHMARK ELECTRONICS INC"  "WESTERN DIGITAL CORP"      
## [1] "--------------------------"
## [1] "Companies loading heavily on topic 2 are"
## [1] "FACEBOOK INC"  "ECHOSTAR CORP" "YAHOO INC"     "AOL INC"       "GOOGLE INC"   
## [1] "--------------------------"
## [1] "Companies loading heavily on topic 3 are"
## [1] "FRONTIER COMMUNICATIONS CORP" "WINDSTREAM HOLDINGS INC"      "LEVEL 3 COMMUNICATIONS INC"   "MANTECH INTL CORP"            "CENTURYLINK INC"             
## [1] "--------------------------"
## [1] "Companies loading heavily on topic 4 are"
## [1] "FIRST SOLAR INC"        "SANDISK CORP"           "SUNPOWER CORP"          "APPLIED MATERIALS INC"  "ADVANCED MICRO DEVICES"
## [1] "--------------------------"
## [1] "Companies loading heavily on topic 5 are"
## [1] "AUTOMATIC DATA PROCESSING"   "DST SYSTEMS INC"             "COMPUTER SCIENCES CORP"      "CERNER CORP"                 "INTL BUSINESS MACHINES CORP"
## [1] "--------------------------"
## [1] "Companies loading heavily on topic 6 are"
## [1] "SPRINT CORP"                  "TELEPHONE & DATA SYSTEMS INC" "INTL GAME TECHNOLOGY"         "BROCADE COMMUNICATIONS SYS"   "LEAP WIRELESS INTL INC"      
## [1] "--------------------------"

结论

潜在主题1

主要讲与产品制造及其需求-供应链有关的风险。

潜在主题2

主要讲在线和移动广告相关的主题。

潜在主题3

该潜在主题讲以与股息和养老金相关成本相关的风险。此外，我们还可以看到与宽带和有线电视运营商相关的风险。

潜在主题4

该潜在主题讲与太阳能行业财务/合并相关的风险。

潜在主题5

该潜在主题是卫生部门，并讨论与实施政府法规有关的风险。

参考资料

可下载资源

关于作者

Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。

本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。

非常感谢您阅读本文，如需帮助请联系我们！

R语言主题模型LDA评估公司面临的风险领域与可视化

随着越来越多的数据被数字化，获取信息变得越来越困难。

目的

分析的意义

分析

Topic Model

LDA算法

使用LDAvis可视化拟合模型

自然语言处理NLP：情感分析疫情下的新闻数据

结论

参考资料

相关文章

R语言主题模型LDA评估公司面临的风险领域与可视化

随着越来越多的数据被数字化，获取信息变得越来越困难。

目的

分析的意义

分析

Topic Model

LDA算法

使用LDAvis可视化拟合模型

自然语言处理NLP：情感分析疫情下的新闻数据

结论

参考资料

相关文章

关注有关新文章的微信公众号