什么是PCR?(PCR = PCA + MLR)
PCR是处理许多 x 变量的回归技术
• 给定 Y 和 X 数据:
• 在 X 矩阵上进行 PCA
– 定义新变量:主成分(分数)
• 在 多元线性_回归_(_MLR_) 中使用这些新变量中的一些来建模/预测 Y
• Y 可能是单变量或多变量。
在响应变量Y与p个解释变量的回归模型中,当解释变量间具有较强的多重共线性时,利用经典的回归方法求回归系数的最小二乘估计,一般效果较差。主成份回归的主要思想是首先通过主成分分析来精简变量,将多个相关的原始变量指标转化为几个独立的综合指标,然后将其作为主成分的观测值,并建立回归模型,以简化回归方程的结构。
主成分回归可以解决变量间共线性的问题,但也给回归模型的解释带来一定的复杂性,因为主成分是原始变量的线性组合,不是直接观测的变量,其含义有时不明确。在求得主成分回归方程后,经常又适用逆变换将其变为原始变量的回归方程。当原始变量间有较强的多重共线性,其主成分又有特殊的含义时,采用主成分回归的效果往往较好。
例子
# 对数据 set.seed(123) da1 <- marix(c(x1, x2, x3, x4, y), ncol = 5, row = F)
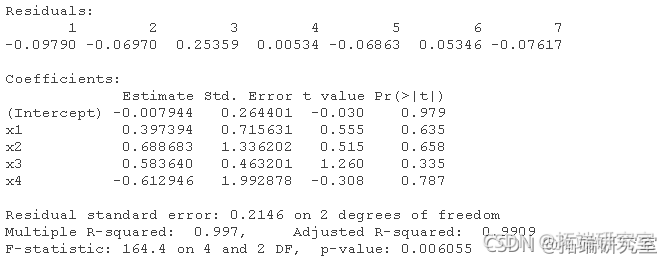
多元线性回归和逐步剔除变量,手动:
# 对于data1:(正确的顺序将根据模拟情况而改变)。 lm(y ~ x1 + x2 + x3 + x4) lm(y ~ x2 + x3 + x4) lm(y ~ x2 + x3) lm(y ~ x3)
可下载资源
作者


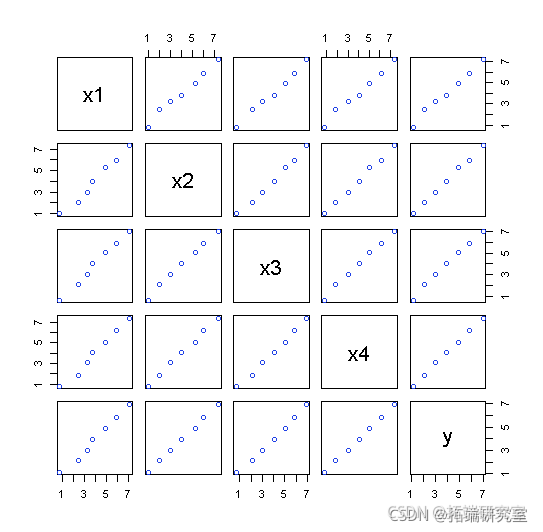
配对关系图
pais(atix, ncol = 5, byrow = F

如果重复:
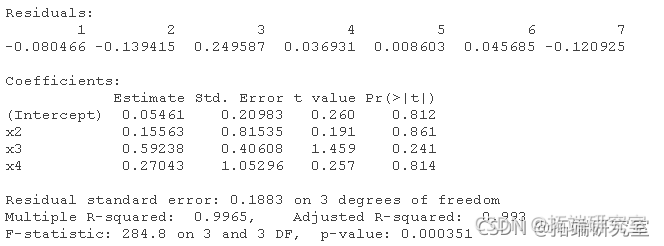
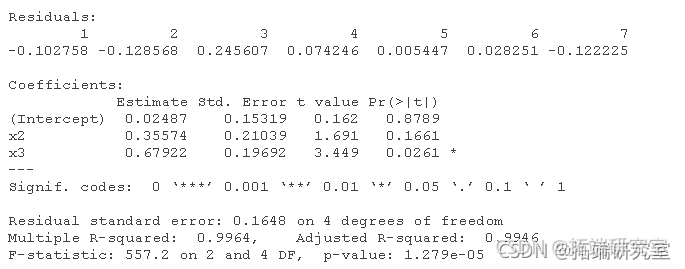
# 对于data2: lm(y ~ x1 + x2 + x3 + x4) lm(y ~ x1 + x2 + x4) lm(y ~ x2 + x4) lm(y ~ x2)




数据集 2 的绘图:
使用四个 x 的均值作为单个变量来分析两个数据集:
xn1 <- (dt1\[,1\] + a1\[,2\] + at1\[,3\] + dt1\[,4\])/4 lm(data1\[,5\] ~ xn1) lm(data2\[,5\] ~ xn2)


检查一下X数据的PCA的载荷loading是什么。
随时关注您喜欢的主题
# 几乎所有的方差都在第一主成分解释。 prnmp(dt1\[,1:4\])

# 第一个成分的载荷 picp(dta1\[,1:4\])$lads\[,1\]

它们几乎相同,以至于第一个主成分本质上是四个变量的平均值。让我们保存一些预测的 beta 系数 – 一组来自数据 1 的完整集和一组来自均值分析的:
c1 <- smry(lm(dta1\[,5\] ~ dta1\[,1\] + dta1\[,2\] + ata1\[,3\] + dt1\[,4\]))$coficns\[,1\] f <- summry(rm2)$cefets\[,1\]
我们现在模拟三种方法(完整模型、均值(=PCR)和单个变量)在 7000 次预测中的表现:
# 对预测进行模拟。 误差<- 0.2 xn <- (x1 + x2 + x3 + x4)/4 yt2 <- cf\[1\] + cf\[2\] * xn yht3 <- cf\[1\] + cf\[2\] * x3 bro(c(um((y-hat)^2)/7000 min = "平均预测误差平方")
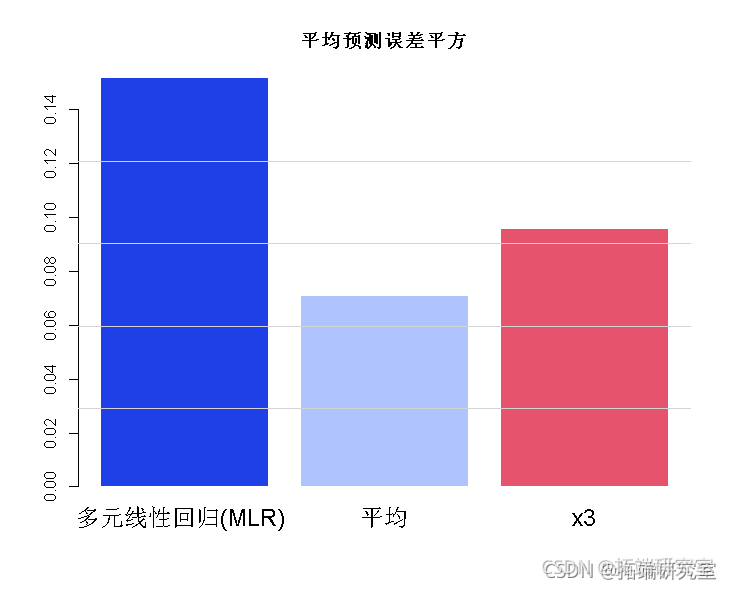
PCR 分析误差最小。
示例:光谱类型数据
构建一些人工光谱数据:(7 个观测值,100 个波长)
# 光谱数据实例 mapot(t(spcra) ) mtlnes(t(spcra))
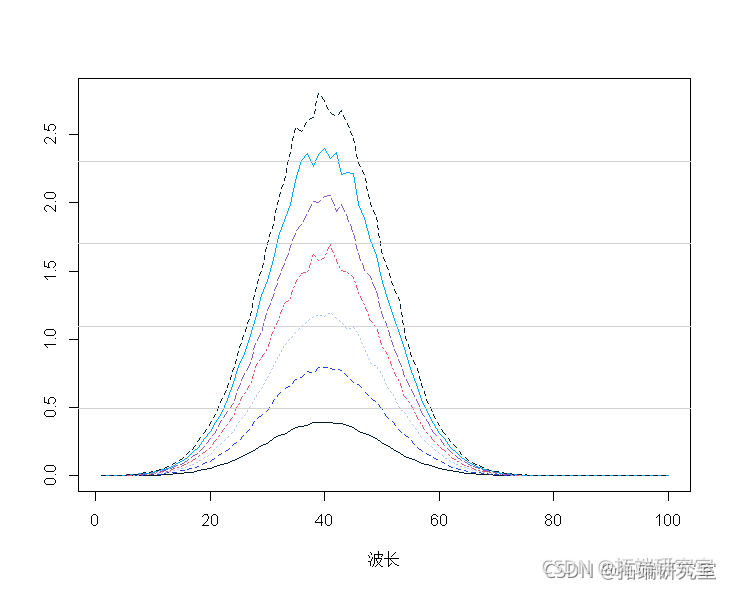
平均光谱表明:
mtpot(t(secra)) malies(t(spcta)) mnp <- apply(spcra, 2, mean) lines(1:100, mnp, lwd = 2)
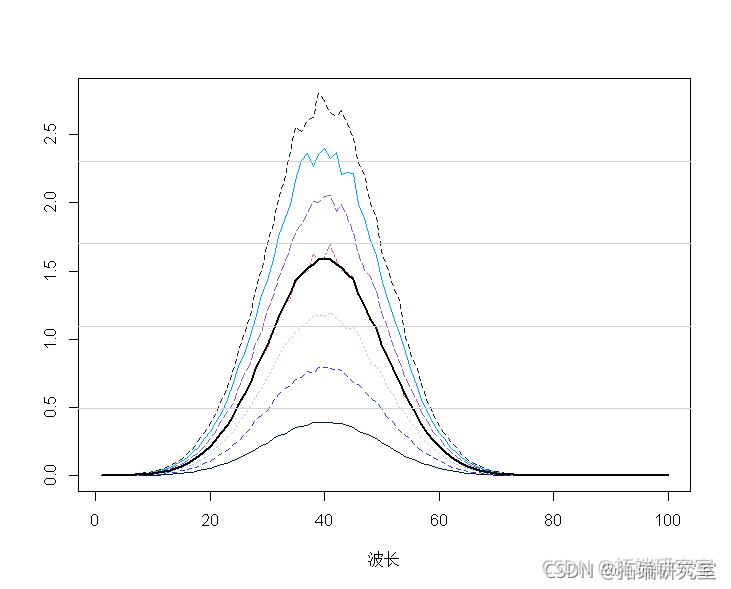
平均中心光谱:
spcamc<-scae(spcta,scale=F) plot(t(spermc),tpe="")

标准化光谱:
sptracs<-scale(spetra,scale=T,center=T) matott(specrams),tye="n", matlies(t(sectramcs))
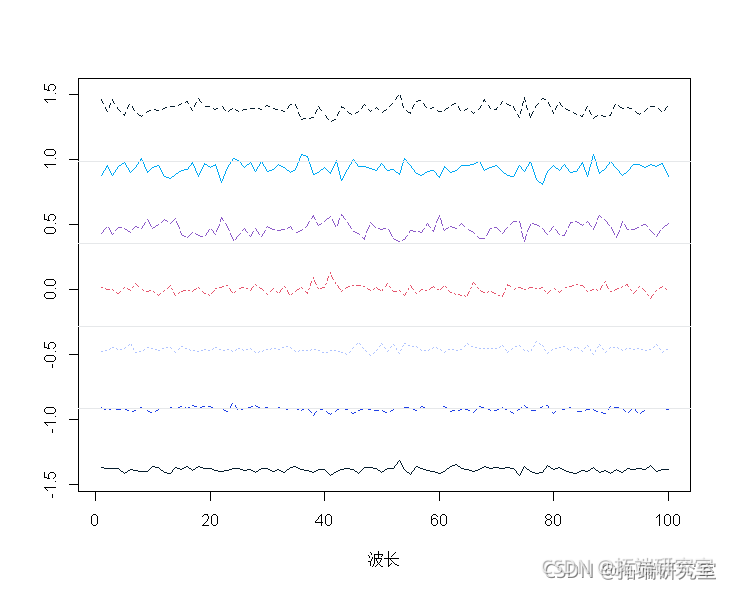
# 用特征函数对相关矩阵做PCA。 pcaes <- eien(cor(spra)) ladigs <- pces$vectors\[,1\]. score <- peramcs%*%t(t(lodis1)) pred <- soes1 %*% loadings1 ## 1-PCA预测值转换为原始尺度和平均值。 mtrx(repeasp, 7), nro=7, brw=T)
在单个概览图中收集的所有图:
par(mfrow = c(3, 3) matlot(t(sectr)

PCR是什么?
• 数据情况:

• 用A 主成分t1、t2… 做MLR而不是所有(或部分)x。
• 多少个成分:通过交叉验证确定。
怎么做?
1. 探索数据
2. 进行建模(选择主成分数量,考虑变量选择)
3. 验证(残差、异常值、影响等)
4. 迭代 2. 和 3。
5. 解释、总结、报告。
6. 如果相关:预测未来值。
交叉验证
• 忽略一部分观察值
• 在剩余(减少的)数据上拟合模型
• 预测模型遗漏的观察值:yˆi,val
• 对所有观察值依次执行此操作并计算总体模型性能:
 (预测的均方根误差)
(预测的均方根误差)
最后:对所有选择的分量(0、1、2、…、… )进行交叉验证并绘制模型性能
barplot(names.arg)

选择最佳成分数:
• 总体误差最小的主成分。
重采样
• 交叉验证 (CV)
•留一法(_Leave-On_e-_Out_,简称LOO)
• Bootstrapping
• 一个很好的通用方法:
– 将数据分成训练集和测试集。
– 在训练数据上使用交叉验证
– 检查测试集上的模型性能
– 可能:重复所有这些多次(重复双交叉验证)
交叉验证 – 原则
• 最小化预期预测误差:
平方预测误差 = Bias2 +方差
• 包括“许多”PC主成分:低偏差,但高方差
• 包括“很少”PC 主成分:高偏差,但低方差
• 选择最佳折衷!
验证 – 存在于不同的级别
1. 分为 3 个:训练(50%)、验证(25%)和测试(25%)
2. 拆分为 2:校准/训练 (67%) 和测试 (33%)
训练中,CV/bootstrap •更常用
3. 没有 “固定分割”,而是通过CV/bootstrap反复分割,然后在每个训练组内进行CV。
4. 没有分割,但使用(一级)CV/bootstrap。
5. 只对所有数据进行拟合–并检查误差。
示例:汽车数据
# 例子:使用汽车数据。 # 将X矩阵定义为数据框中的一个矩阵。 mtas$X <- as.ix(mcas\[, 2:11\]) # 首先,我们考虑随机选择4个属性作为测试集 mtcrs_EST<- mtcrs\[tcars$rai == FASE,\] 。 tcaTRAIN <- mtars\[tcarstrai == TUE,\] 。
现在所有的工作都在 训练数据集上进行。
探索数据
我们之前已经这样做了,所以这里不再赘述
数据建模
使用pls软件包以最大/大量的主成分运行PCR。
# 使用pls软件包,以最大/较大的成分数运行PCR。 pls(lomg ~ X , ncop = 10, dta = marsTRAN, aliaon="LOO")
初始图集:
# 初始化的绘图集。 par(mfrow = c(2, 2) plot(mod)
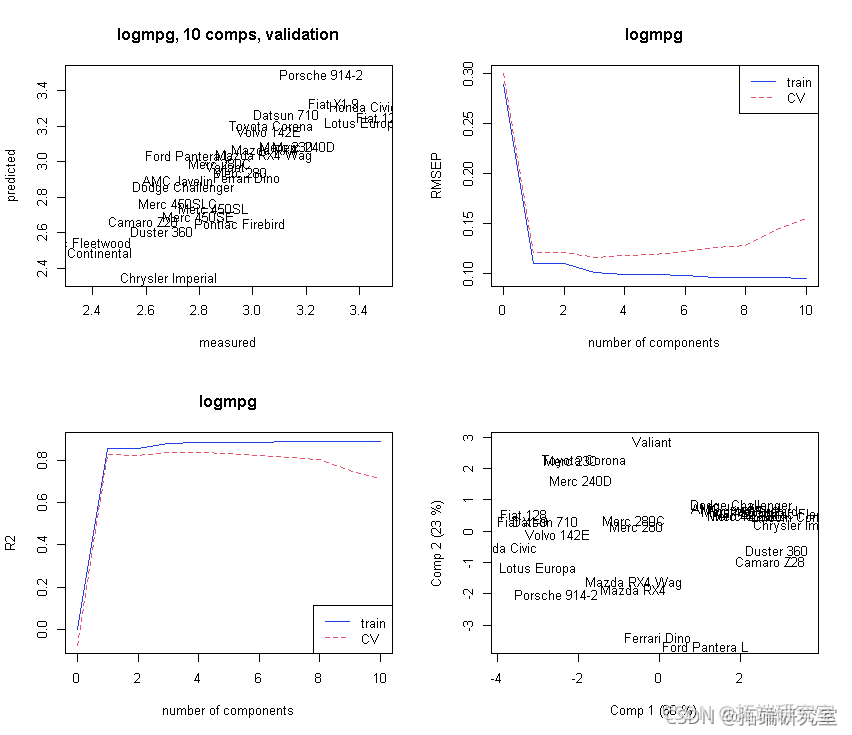
主成分的选择:
# 主成分的选择。 # 分段的CV会得到什么。 modseCV <- pcr(lomg ~ X , ncp = 10, dta = marTIN vai ="CV" ) # 初始图集。 par(mfrow = c(1, 2)) plot(odsC, "vadaion")
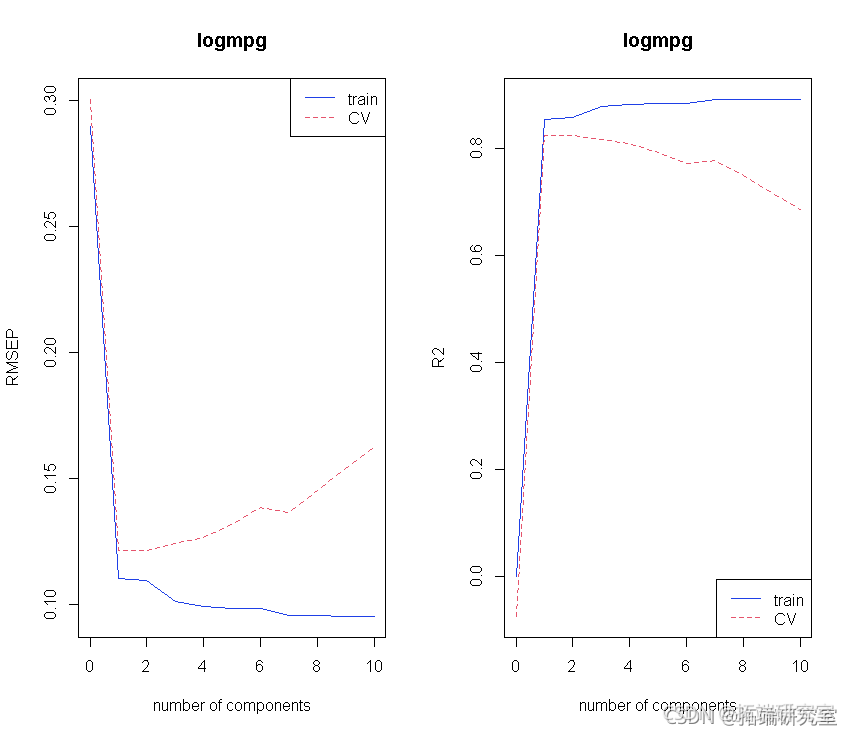
让我们看看更多的主成分:
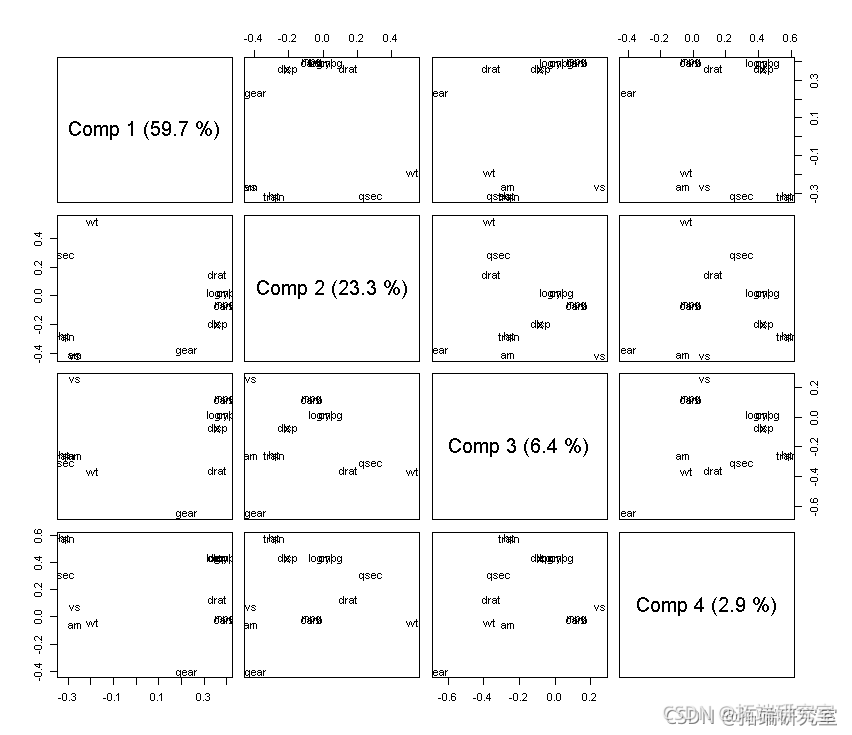
# 让我们看看更多的主成分。 # 分数。 scre(mod)

#负荷 loading(md,cms = 1:4)
我们选择 3 个主成分:
# 我们选择4个成分 m <- ncmp = 3, data = mrs_TAI vdon = "LOO", akknie = RUE
然后: 验证:
让我们验证更多:使用 3 个主成分。我们从中获取预测的残差,因此这些是(CV)验证版本!
oit <- ppo(mod3, whih = "litin") plot(obft\[,2\], Rsds) # 为了绘制残差与X-杠杆的对比,我们需要找到X-杠杆。 # 然后找到杠杆值作为Hat矩阵的对角线。 # 基于拟合的X值。 Xf <- sors(md3) plot(lvge, abs(Rsidals)) text(leage, abs(Reuls))
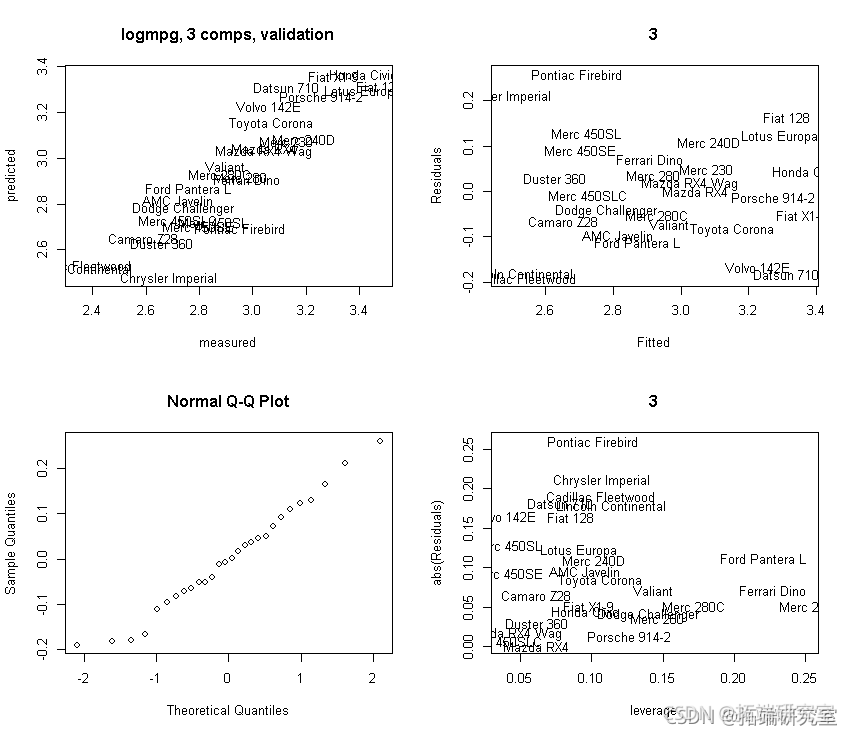
# 让我们也绘制一下残差与每个输入X的关系。
for ( i in 2:11){
plot(res~masAN\[,i\],type="n")
}

解释/结论
现在让我们看一下结果——“解释/结论”:
# 现在我们来看看结果 - 4) "解释/结论" par(mfrw = c(2, 2)) # 绘制具有Jacknife不确定性的系数。 obfi <- red(mod3,, wich = "vltn) abe(lm(ft\[,2\] ~ fit\[,1\]) plt(mo3, ses = TUE,)
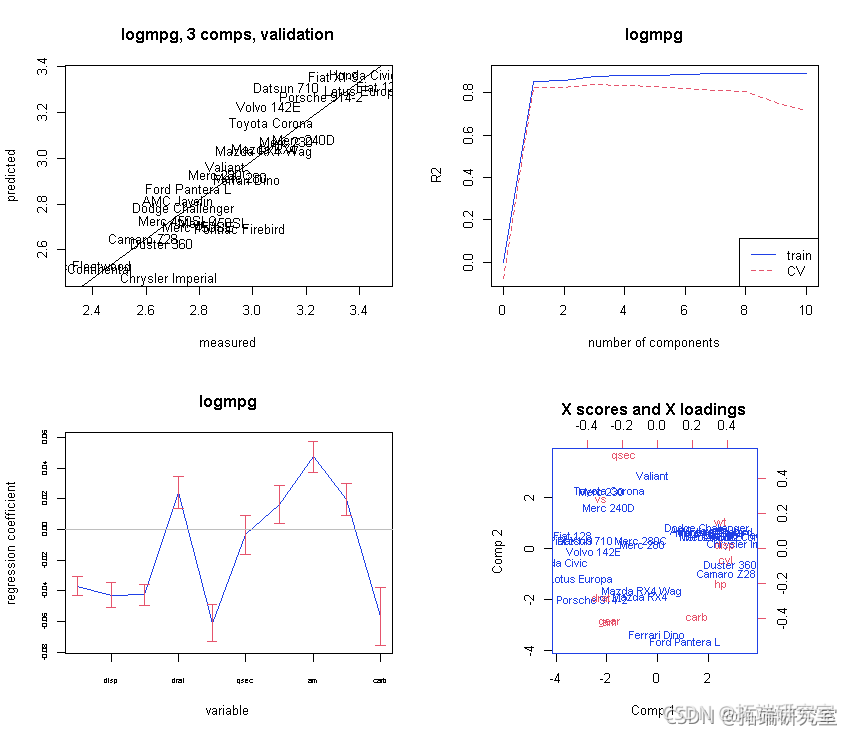
# 最后是一些输出 test(mo3, nm = 3)

预测
# 现在让我们试着预测TEST集的4个数据点。 prdit(md3, nwaa =TEST) plt(TEST$lgg, pes)
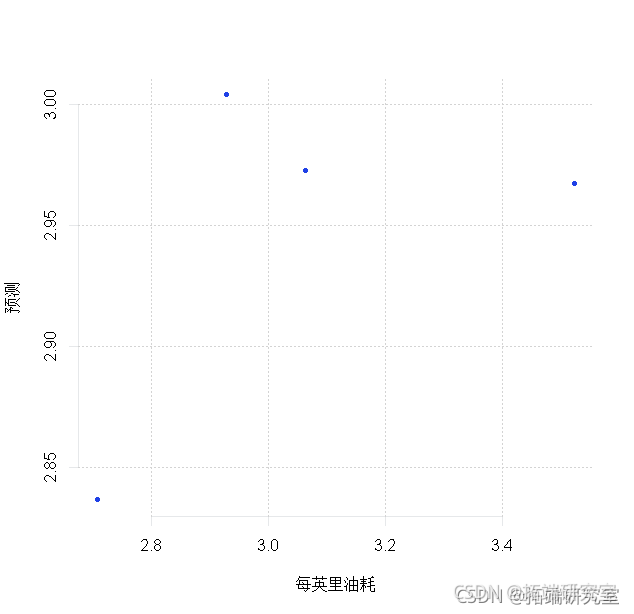
rmsep <- sqrt(men(log - prd)^2)) rmsep

可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 CrewAI与GPT融合多智能体MAS与实时数据预测2026T20世界杯胜者|附代码数据
CrewAI与GPT融合多智能体MAS与实时数据预测2026T20世界杯胜者|附代码数据 LLM嵌入K-Means、DBSCAN聚类、PCA主成分分析新闻文本聚类研究|附代码数据
LLM嵌入K-Means、DBSCAN聚类、PCA主成分分析新闻文本聚类研究|附代码数据 2026汽车行业趋势洞察和典型增长市场解析:轻量化、智能化、出海|附600+份报告PDF、数据、可视化模板汇总下载
2026汽车行业趋势洞察和典型增长市场解析:轻量化、智能化、出海|附600+份报告PDF、数据、可视化模板汇总下载 2025智能汽车产业深度研究报告:L3自动驾驶、Robotaxi|附680+份报告PDF、数据、可视化模板汇总下载
2025智能汽车产业深度研究报告:L3自动驾驶、Robotaxi|附680+份报告PDF、数据、可视化模板汇总下载



