
本文描述了如何 使用内置 R 执行主成分分析 ( PCA )。
您将学习如何 使用 PCA_预测_ 新的个体和变量坐标。我们还将提供 _PCA 结果_背后的理论。
在 R 中执行 PCA 有两种通用方法:
PCA只是一种思想,核心就是线性变化,线性代数里的工具只是一种高效的实现PCA的手段,但并不是唯一的工具。
PCA的核心思想:假设我们的数据有D1, D2,···,Dn个维度,PCA就是要构造一个线性变换,PCi = W1D1 + W2D2 +···+ WnDn,Wj就是第j维度在第i个PC中的权重。找PC有先后顺序,我们总是先找总方差最大的PC,方差解释度是统计里最重要的一个概念。然后我们再找与前一个PC线性无关的能解释最多方差的下一个PC,以此类推,知道得到所有的n个PC。最终的结果就是原先的n个维度通过线性变换,变成了新的n个线性无关的按方差解释度排序的PC。主成分中的“主principal”针对的就是方差解释度。
- 谱分解 ,检查变量之间的协方差/相关性
- 检查个体之间的协方差/相关性的_奇异值分解_
根据 R 的帮助,SVD 的数值精度稍好一些。
可视化
创建基于 ggplot2 的优雅可视化。
演示数据集
我们将使用运动员在十项全能中的表现数据集,这里使用的数据描述了运动员在两项体育赛事中的表现
数据描述:
一个数据框,包含以下13个变量的27个观测值。
X100m
一个数字向量
跳远
一个数字向量
投篮
一个数字向量
高跳
一个数字向量
X400m
数字向量
X110m.hurdle
一个数字向量
飞碟
一个数字向量
撑杆跳高
一个数字向量
绳索
数字向量
X1500米
数字向量
级别
与等级相对应的数字向量
点
一个数字向量,指定获得的点数
运动会
水平变量 Decastar OlympicG
简而言之,它包含:
- 训练个体(第 1 到 23 行)和训练变量(第 1 到 10 列),用于执行主成分分析
- 预测个体(第 24 至 27 行)和预测变量(第 11 至 13 列),其坐标将使用 PCA 信息和通过训练个体/变量获得的参数进行预测。
加载数据并仅提取训练的个体和变量:
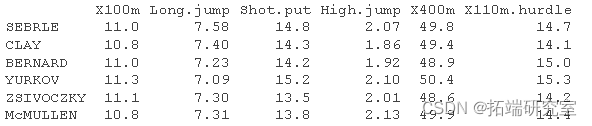
计算 PCA
在本节中,我们将可视化 PCA。
- 进行可视化
- 计算 PCA
prcomp
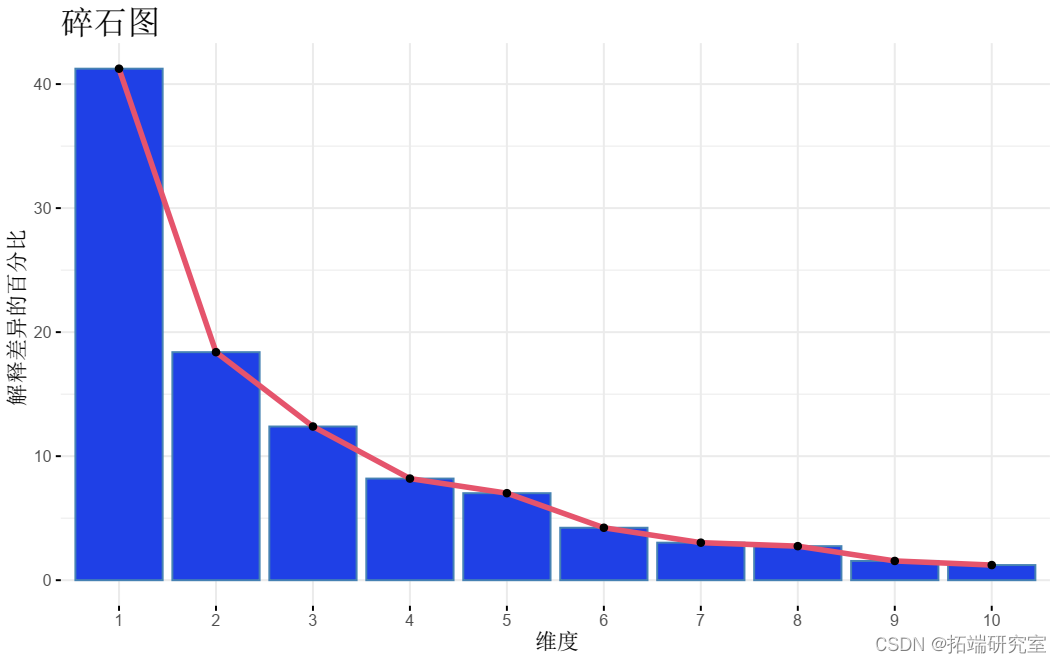
- 可视化 特征值 (_碎石图_)。显示每个主成分解释的方差百分比。
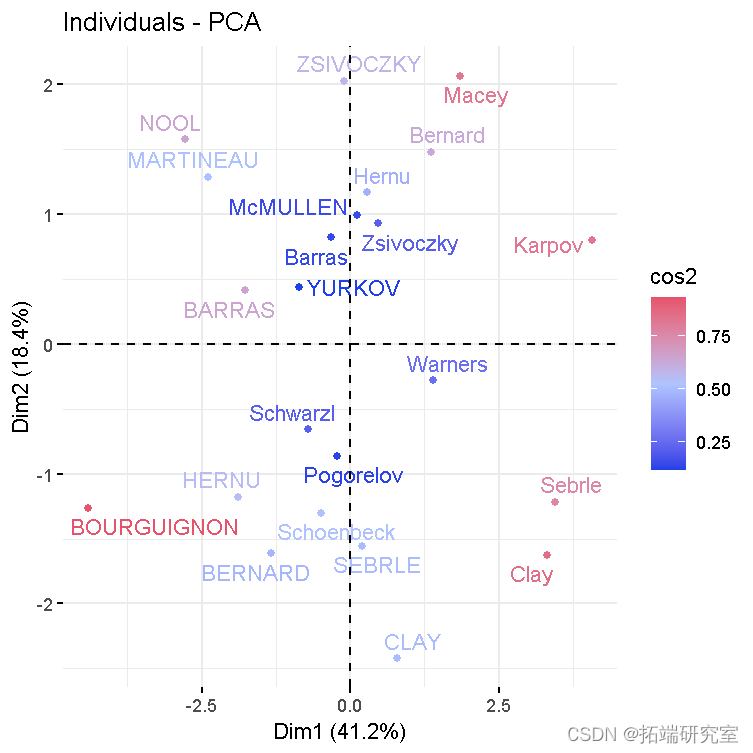
- 具有相似特征的个人被归为一组。
viz(res )
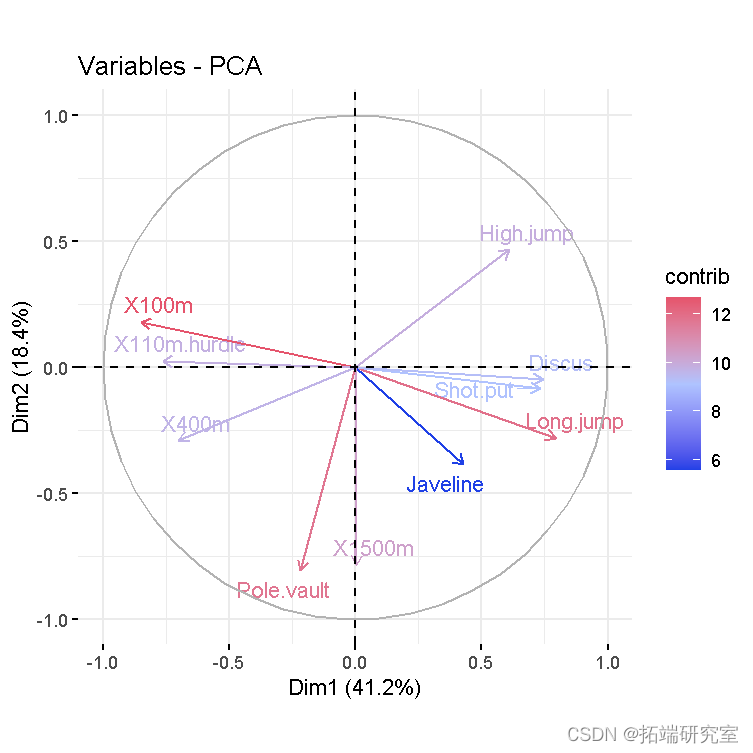
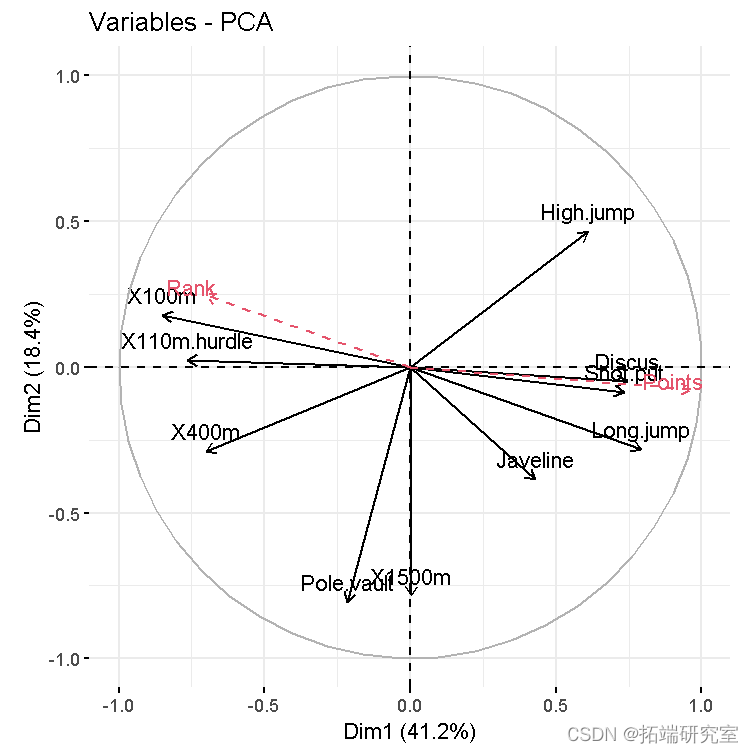
- 变量图。正相关变量指向图的同一侧。负相关变量指向图表的相反两侧。
vzpca(res )
head(dec)
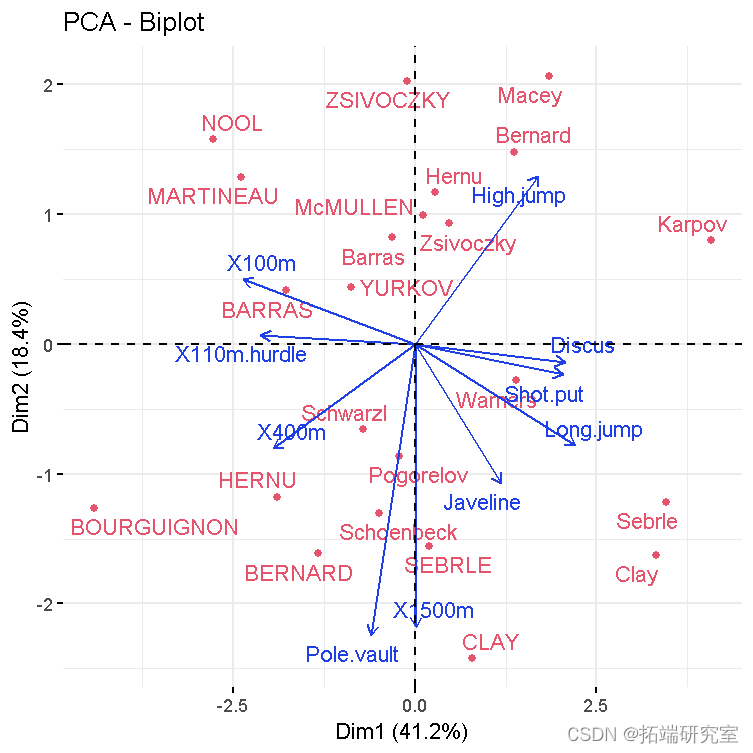
- 个体和变量的双标图
fvbiplot(res )
随时关注您喜欢的主题
PCA 结果
# 特征值 eigva # 变量的结果 coord # 坐标 contrib # 对PC的贡献 cos2 # 代表性的质量 # 个人的结果 coord # 坐标 contrib # 对PC的贡献 cos2 # 代表性的质量
使用 PCA 进行预测
在本节中,我们将展示如何仅使用先前执行的 PCA 提供的信息来预测补充个体和变量的坐标。
预测个人
- 数据:第 24 到 27 行和第 1 到 10 列。新数据必须包含与用于计算 PCA 的活动数据具有相同名称和顺序的列(变量)。
# 预测个体的数据 in <- dec\[24:27, 1:10\]

- 预测新个体数据的坐标。使用 R 基函数 predict ():
predict

- 包括补充个人在内的个人图表:
# 活跃个体的图谱 fvca_ # 添加补充个体 fdd(p)
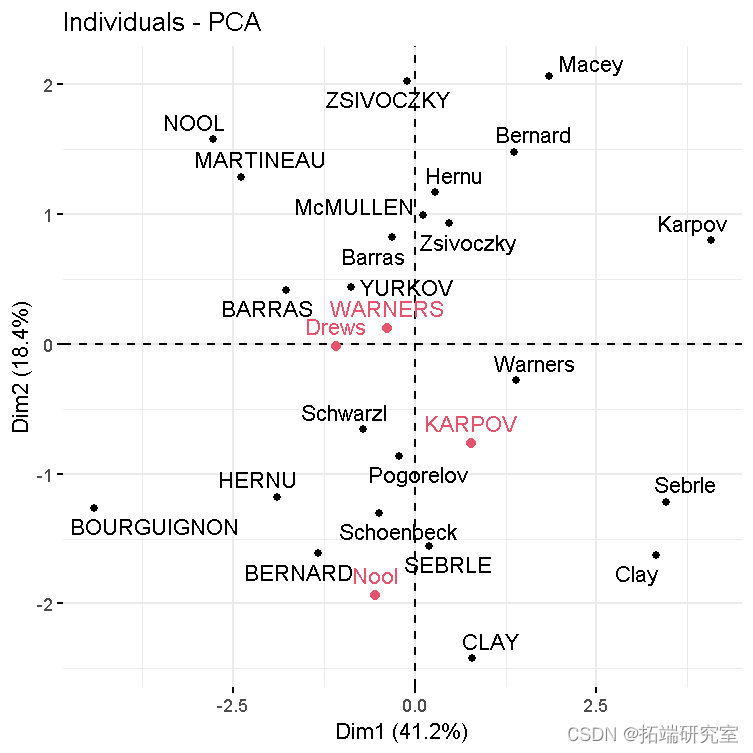
个体的预测坐标可以计算如下:
- 使用 PCA 的中心和比例对新的个人数据进行中心化和标准化
- 通过将标准化值与主成分的特征向量(载荷)相乘来计算预测坐标。
可以使用下面的 R 代码:
# 对补充个体进行居中和标准化 ined <- scale # 个体个体的坐标 rtaton ird <- t(apply)

补充变量
定性/分类变量
数据集 在第 13 列包含与比赛类型相对应的 补充定性变量 。
定性/分类变量可用于按组为样本着色。分组变量的长度应与活跃个体的数量相同。
groups <- as.factor fvnd(res.pca )
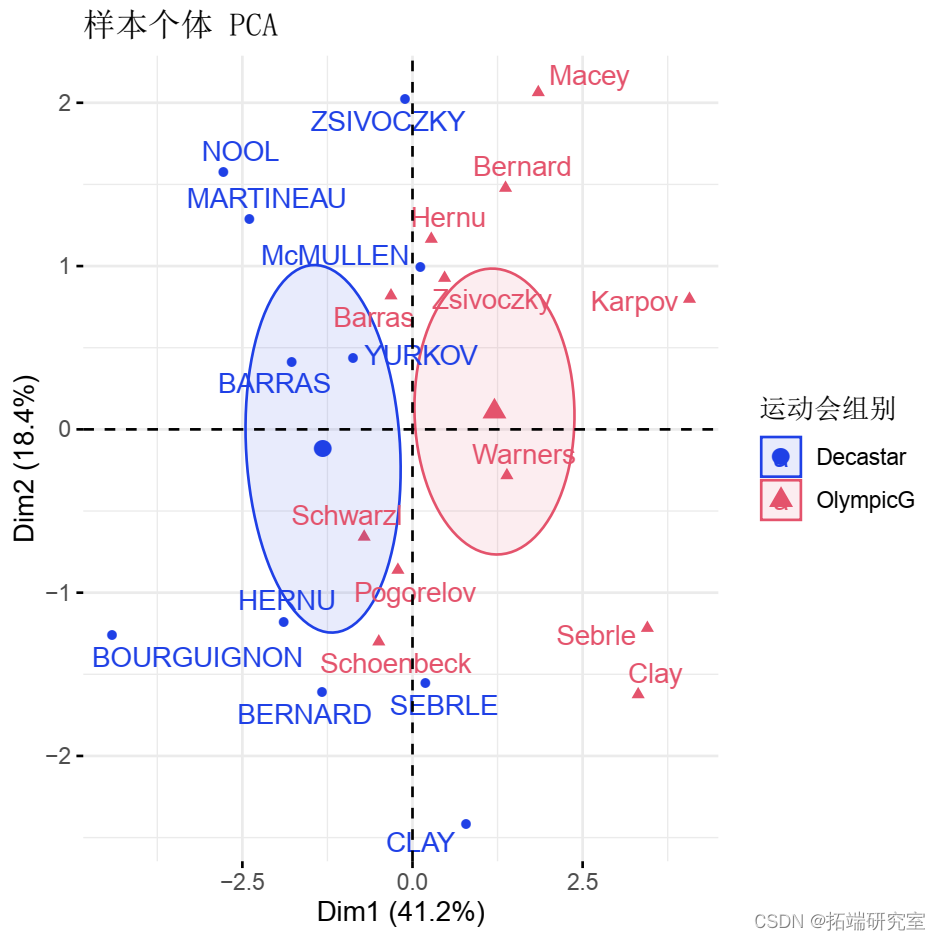
计算分组变量水平的坐标。给定组的坐标计算为组中个体的平均坐标。
library(magrittr) # 管道函数%>%。 # 1. 单个坐标 getind(res) # 2. 组的坐标 coord %>% > as\_data\_frame%>% selec%>% mutate%>% group_b %>%
数据:11:12 栏。应与活跃个体的数量相同(此处为 23)

定量变量
quup <- dec\[1:23, 11:12\] head(quup .sup)
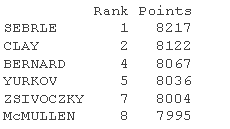
给定定量变量的坐标被计算为定量变量与主成分之间的相关性。
# 预测坐标并计算cos2 quaord <- cor quaos2 <- qord^2 # 变量的图形,包括补充变量 p <- fviar(reca) fvdd(p, quord, color ="blue", geom="arrow")
PCA 结果背后的理论
变量的 PCA 结果
在这里,我们将展示如何计算变量的 PCA 结果:坐标、cos2 和贡献:
var.coord= 载荷 * 分量标准差var.cos2= var.coord ^ 2var.contrib. 变量对给定主成分的贡献为(百分比):(var.cos2 * 100)/(成分的总 cos2)
# 计算坐标 #:::::::::::::::::::::::::::::::::::::::: logs <- rotation sdev <- sdev vad <- t(apply)
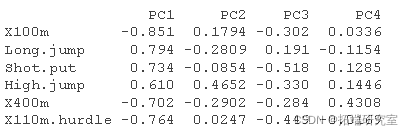
# 计算 Cos2 #:::::::::::::::::::::::::::::::::::::::: vaos2 <- vard^2 head(vars2\[, 1:4\])
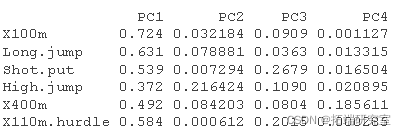
# 计算贡献 #:::::::::::::::::::::::::::::::::::::::: comos2 <- apply cnrib <- function var.otrb <- t(apply) head(vaib\[, 1:4\])
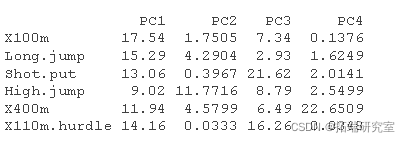
PCA 结果
ind.coord= res.pca$x- 个人的 Cos2。两步:
- 计算每个个体与 PCA 重心之间的平方距离:d2 = [(var1\_ind\_i – mean\_var1)/sd\_var1]^2 + …+ [(var10\_ind\_i – mean\_var10)/sd\_var10]^2 + …+..
- 将 cos2 计算为 ind.coord^2/d2
- 个人对主成分的贡献:100 (1 / number\_of\_individuals)(ind.coord^2 / comp_sdev^2)。请注意,每列所有贡献的总和为 100
# 个人的坐标 #:::::::::::::::::::::::::::::::::: inod <- rpa$x head(in.c\[, 1:4\])
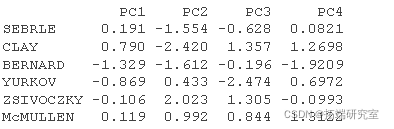
# 个人的Cos2 #::::::::::::::::::::::::::::::::: # 1.个体与#PCA重心之间距离的平方 # PCA重心的平方 ceer<- center scle<- scale d <- apply(decaive,1,gnce, center, scale) # 2. 计算cos2。每一行的总和为1 is2 <- apply(inrd, 2, cs2, d2) head(is2\[, 1:4\])
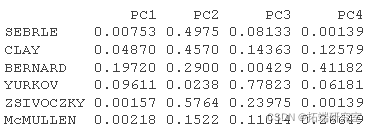
# 个人的贡献 #::::::::::::::::::::::::::::::: inib <- t(apply(iord, 1, conib, sdev, nrow)) head(inib\[, 1:4\])
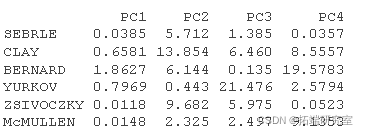
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 LLM嵌入K-Means、DBSCAN聚类、PCA主成分分析新闻文本聚类研究|附代码数据
LLM嵌入K-Means、DBSCAN聚类、PCA主成分分析新闻文本聚类研究|附代码数据 Python语义关键词异构图谱TF-IDF、GCN-GAE图卷积自编码器、PCA、t-SNE及KL散度分析中国发明专利数据
Python语义关键词异构图谱TF-IDF、GCN-GAE图卷积自编码器、PCA、t-SNE及KL散度分析中国发明专利数据 Python神经网络、随机森林、PCA、SVM、KNN及回归实现ERα拮抗剂、ADMET数据预测|附代码数据
Python神经网络、随机森林、PCA、SVM、KNN及回归实现ERα拮抗剂、ADMET数据预测|附代码数据 Python、Amos汽车用户满意度数据分析:BERT情感分析、CatBoost、XGBoost、LightGBM、ACSI、GMM聚类、SHAP解释、MICE插补、PCA降维、熵权法
Python、Amos汽车用户满意度数据分析:BERT情感分析、CatBoost、XGBoost、LightGBM、ACSI、GMM聚类、SHAP解释、MICE插补、PCA降维、熵权法
