本文中,我们讨论了一个将Poisson过程与Wiener过程结合在一起的最佳算法的问题。
实际上,为了生成泊松过程,我们总是习惯于模拟跳跃之间的持续时间。我们使用给定时间间隔内跳跃的均匀性,该条件取决于跳跃的次数。
可下载资源
首先,我们可以生成一个可能具有漂移的维纳过程,然后在其旁边,我们可以生成指数定律(这将对应于跳跃之间的时间),还可以生成跳跃幅度 。
我们在这里
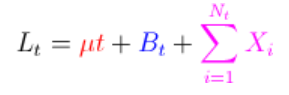
要么 。我们首先通过注意
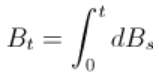
其中增量是高斯(均值和方差),并且彼此独立。
至于跳跃之间的持续时间,它们是独立的平均指数定律。这是代码,
n=1000
h=1/n
lambda=5
set.seed(2)
W=c(0,cumsum(rnorm(n,sd=sqrt(h))))
W=rexp(100,lambda)
N=sum(cumsum(W)<1)
T=cumsum(W[1:N])
X=-rexp(N)
问题是对于维纳过程,我们必须离散化,而对于复合泊松过程,我们不能离散化。但是,他们有相同的时间范围。第一种方法是建立trunc函数
W[trunc(n*t)+1]+sum(X[T<=t])+lambda*t
然后可视化
L=Vectorize(Lt
plot(u,L(u),type="l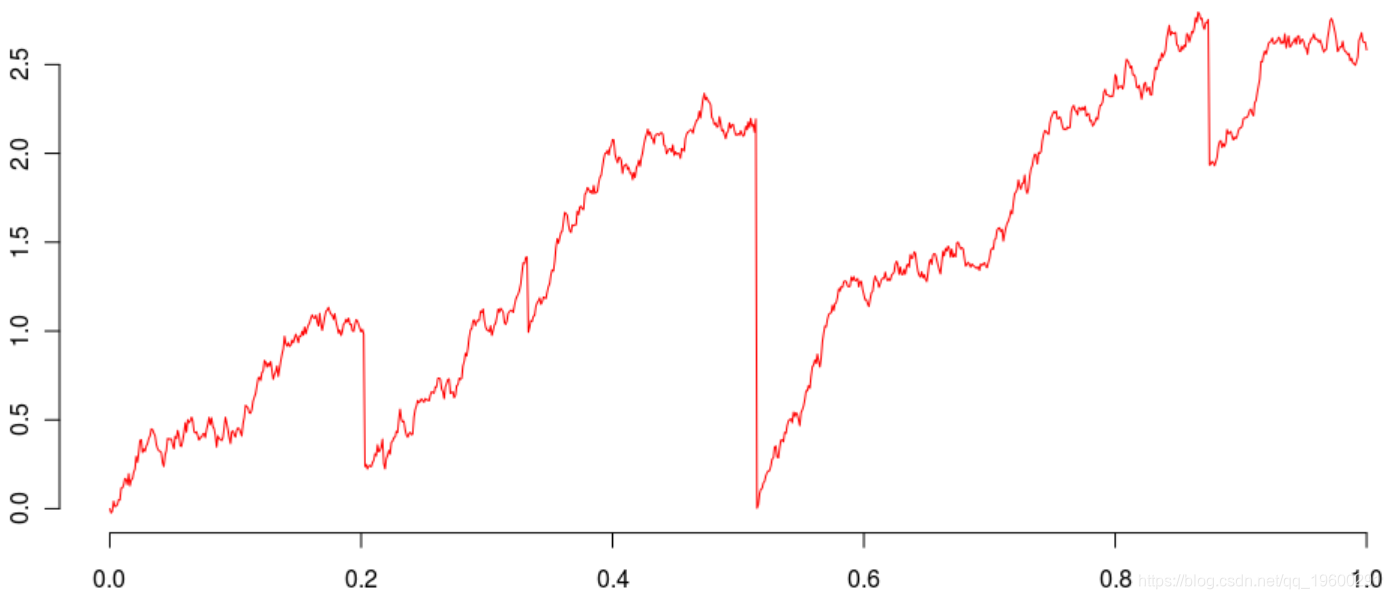
另一种可能性是使用我在引言中提到的泊松过程的均匀性。因为泊松过程满足一个特性:如果是第i个跳跃发生的日期,则有条件基于以下事实: ,变量
![]()
对应于的订单统计 独立变量,是均匀分布
该属性可在 Wolff(1982)中找到。我们从一个(单个)跳跃开始,
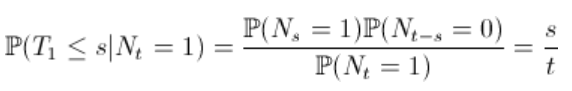
即我们找到一个统一的分布函数。然后,我们进行2跳,3跳等迭代。
这个想法的R翻译很简单
N=rpois(1,lambda)
然后,一种策略是离散化Poisson过程,与Wiener过程的时间步长相同,
indice=trunc(T*n
processus=W+cumsum(saut)+lambda*u我们发现与以前相同的轨迹
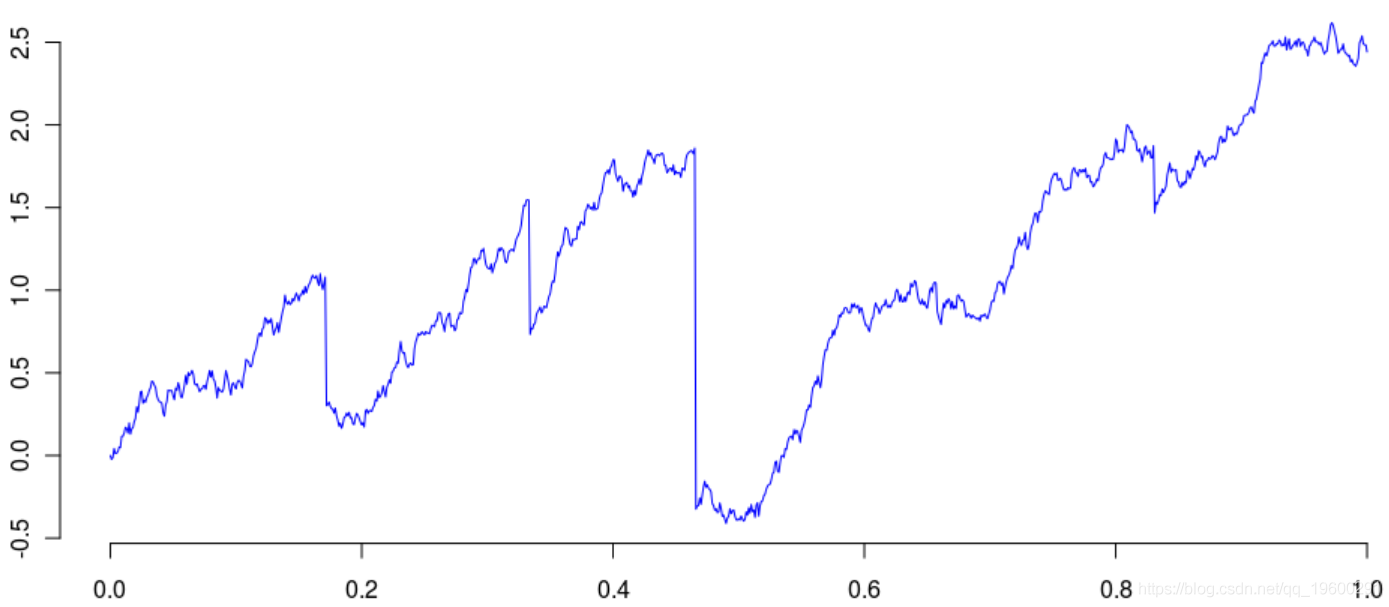
通过此过程,我们不能在同一时间间隔内有两次跳跃。泊松过程的特征是
![]()
因此,极少有机会同时进行两次跳跃,尤其是在时间步长较小的情况下。如果我们生成数千条轨迹,那么一次出现问题的可能性就可以忽略不计。
有一个主意是采用离散均匀分布,
T=c(0,sort(sample((1:(n-1)/n),size=N,replace=FALSE)))以避免同时发生两次跳跃。
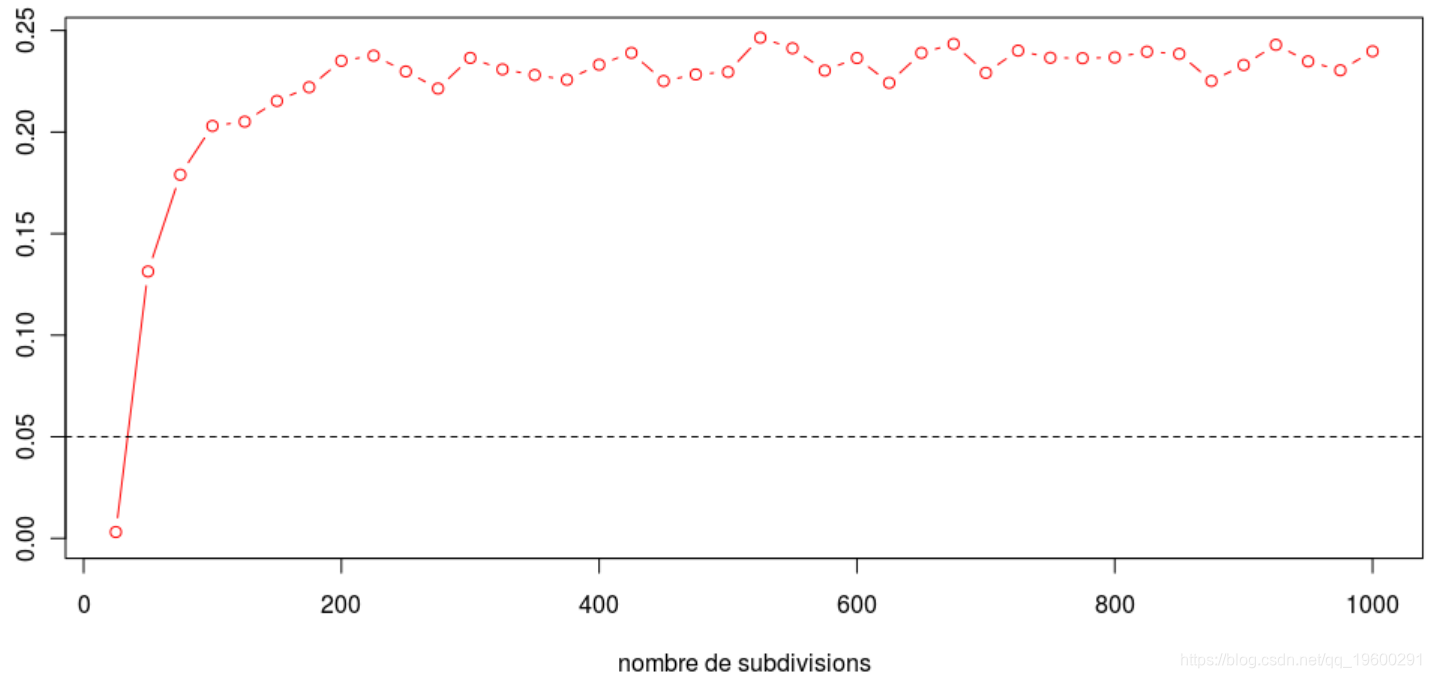
为此,我们可以做一些测试。例如,生成一些模拟以具有一百次跳跃(因此两次跳跃之间的持续时间为一百次),然后进行指数定律检验。
VT=0
for(ns in 1:20){
N=rpois(1我们在这里做了20个循环
lambda=5我想进行一百次观察来进行检验。然后,我们可以进行指数拟合检验,
ks.test(VT[-1],"pexp",lambda)$p.value如果我们重复很多次,则通过更改时间步长(或时间间隔的细分数),实际上,如果时间步长很大(在左下方),我们将通常拒绝,指数定律也是如此。但是很快,这是一个不成立的假设,
我们有两个不错的算法来生成莱维过程。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 Python电动汽车充电网络优化研究——泊松过程、排队、贪心算法、模拟退火、聚类、差分演化DE、双目标动态规划、滚动时域预测控制MPC分析储能调度、电网负荷数据|附代码数据
Python电动汽车充电网络优化研究——泊松过程、排队、贪心算法、模拟退火、聚类、差分演化DE、双目标动态规划、滚动时域预测控制MPC分析储能调度、电网负荷数据|附代码数据 Python蒙特卡罗MCMC:优化Metropolis-Hastings采样策略与Fisher矩阵计算参数推断应用—模拟与真实数据分析
Python蒙特卡罗MCMC:优化Metropolis-Hastings采样策略与Fisher矩阵计算参数推断应用—模拟与真实数据分析 R语言泊松过程及在随机模拟应用可视化
R语言泊松过程及在随机模拟应用可视化 R语言蒙特卡罗Monte Carlo方法进行数值积分和模拟可视化
R语言蒙特卡罗Monte Carlo方法进行数值积分和模拟可视化



