
在这篇文章中,我们将看一下Poisson回归的拟合优度测试。
许多软件包在拟合Poisson回归模型时在输出中提供此测试,或者在拟合此类模型(例如Stata)之后执行此测试,这可能导致研究人员和分析人员依赖它。
可下载资源
在这篇文章中,我们将看到测试通常不会按预期执行,因此,我认为,应该谨慎使用。
在数据分析中,对于定类变量和低测度的定序变量,通常不能使用均值、T检验和方差分析等方法来处理。对于不符合正态分布的定类数据或低测度定序数据,其检验方法是利用交叉表技术分行分列计算交叉点的频数,利用卡方距离实施卡方检验,基于频数和数据分布形态分析不同类别的数据是否存在显著性差异,对于定类数据的对比检验,也叫独立性检验。
低测度数据
对于定类变量,其数值大小和顺序并不代表什么意义,对于定类变量和低测度的定序变量,均值和方差都不能描述变量特征,故不能通过分析其平均值、方差等参数开展数据分析。在做统计分析时,对于这类变量通常需要借助中位数、频数、百分比以及不同分布情况,实现数据描述。对于低测度数据,比较典型的研究是关于结构成分的研究,实际上是一种借助频数来分析数据分布形态,并进而发现数据分布差异性的检验。
拟合及拟合优度
由于低测度数据的特点,直接进行基于均值的检验显然是不行的,于是人们借助数学模型,提出了拟合的概念。所谓拟合,就是分析现有观测变量的分布形态,检查其分布能够与某一期望分布(或标准分布)很好地吻合起来。在数学上,拟合的过程就是寻找能很好地温和当前数据序列的数学模型的过程。为了评价拟合的程度,人们提出了判定拟合有效性的机制,这就是拟合优度。拟合优度也借助检验概率的概念来评价数据拟合的质量。
目前,对于低测度数据序列的处理最常见的分析方法是卡方检验。特别是基于交叉表的卡方检验在数据分析中具有重要的地位,它们都建立在拟合概念的基础上。另外,二项分布、游程检验等单样本检验也可以看做是数据拟合的重要应用。与此同时,对定距或定序变量的分布形态判定,也是数据拟合的应用之一,在分布形态判定过程中所获得的检验概率就是该序列与标准分布形态的拟合优度。
卡方检验
卡方检验的目标就是检查观测值的频数与期望频数之间的差异显著性。由于卡方检验要求便于对个案进行分类并计算频数,因此卡方检验通常基于定类数据或低测度定序数据,并基于它们分类计算个案的实际频数,然后通过实际频数与期望频数的距离,来判定实际频数是否与预期目标存在差异。
卡方距离
由于卡方检验的目标是检查观测频数与期望频数之间的差异性水平,因此卡方检验的核心内容就是计算出观测值的频数与期望频数总体差距的统计量,就是卡方距离。这个距离可以通过“观测值频数与期望频数差值的平方与期望频率之比的累积和”来体现:
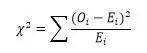
卡方值越大,表示距离越大,差异性越强。可以根据卡方值查表推导出卡方检验的概率值,然后根据概率值判定卡方检验的判断结论。
卡方检验的两种应用
卡方检验有两种基本应用。其一,检验期望分布与实际观测值的差异性。其二,基于交叉表检验两个低测度变量在各自不同的因素水平上的卡方距离,从而实现两个低测度变量的关联性(独立性)检验。
面向期望分布的卡方检验
对于低测度变量,如果从总体中抽取若干样本,构成k个互不相交的子集。这k个子集的观测频数应该服从一个多项分布。当k趋向于无穷时,这个分布应该接近于总体的分布规律。
因此,对于变量X的总体分布,可以从观察样本在各个频段的频数入手。通过观察样本在各个频段的频数分布,可以掌握样本的分布形态。另外,对比它们与预期值的差距,可以掌握变量X是否与预期分布存在显著性差异。
对于检验观测值与期望值在频数上拟合程度的检验,也常常被称为卡方拟合优度检验。例如,现在已经统计出了2013年的招生情况,掌握了2013年学校在各个省份的招生人数。在2015年的招生工作刚刚完成,拿到了全体新生的基本信息后,现在需要分析2015年招生情况是否与2013年的各省招生情况有显著性差异。为此,需要由计算机自动计算出2015年分省招生个案数,并借助卡方公式计算出2015年的分省学生数与2013年分省学生数的卡方值,从而判定二者是否存在显著性差异。
基于K-S检验的分布形态判断就是这样一种用法。在SPSS中,通常使用K-S算法进行单样本的分布形态判断,可以对序列进行正态分布(即常规分布)、均匀分布(即相等分布)、泊松分布、指数分布等分布形态的判定。
基于交叉表的卡方检验
对交叉表中的行变量和列变量之间的关系进行分析是交叉分组下频数分析的重要任务,对低测度的定序变量(或定类变量)交叉分组并计算频数后,可以分析行变量与列变量之间是否存在关系,或者说基于某个变量的不同水平,在另一个变量的不同水平上其频数是否有显著性的差异。基于这一思路,可以获取两个变量之间是否存在一定关联性,关联的紧密程度等更深层次的信息。例如,某公司统计旗下零食产品在超市不同位置的销售量,构造交叉表:
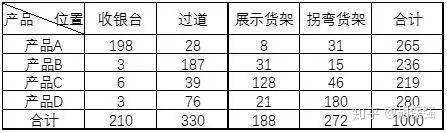
从上表来看,沿着“左上-右下”的对角线方向,数据的量比较大,表示产品的不同种类销量与展示位置之间还是有一定关联性的。
大多数交叉表中的数据不会像上表一样,能那么容易看出其中内在关系,必须借助数据分析的专业手段对交叉表中的频数进行计算,获取其卡方值和检验概率,然后以检验概率值为标准,做出检验结论。对交叉表的统计分析,卡方检验的统计量采用了Pearson卡方统计量标准,其数学定义式为:

在对交叉表的卡方检验中,当获得了交叉表之后,可以根据卡方计算公式计算出整个交叉表的卡方值,然后依据卡方值查相应的统计表,得到此卡方值的检验概率值,进而判断两变量是否相互独立,没有任何关联。
游程检验与随机分布
游程是指在变量序列当中,连续出现相同的值的次数。对于序列“111222223331123333”可以认为有6个游程,依次为“111”、“22222”、“333”、“11”、“2”和“3333”。
游程检验的思路与用途
游程检验是指依据某种规则对数据序列中的个案分组,并记录每个个案的组好;然后,对数据序列按照升序排序,把得到的组号排列起来就构成一个游程序列。对于一个数据序列,如果游程个数达到一定的规模,就认为序列的分布是随机分布。游程检验的目标是检验两种样本的分布是否具有随机性,游程的价值就是判别分布规律的随机程度。
单样本变量值的随机测验中,利用游程数构造检验统计量,分析这个统计量的分布情况,从而能够反映样本所代表的总体的分布是否满足随机性。单样本变量值的随机性检验中,SPSS将利用游程构造Z统计量,并依据正态分布表给出对于的相伴概率值。如果相伴概率值大于显著性水平,则不能拒绝零假设,认为变量值的出现是随机的。
二项分布检验
在现实生活中,很多变量的取值只有两种状态,被称之为二分变量或二项变量。比如,人类性别的取值是男或女,职位应聘结果为成功或失败,投掷硬币的实验结果可以是正面或者反面。凡是只有两种取值状态的变量,都被称为二值变量。对这种变量来说,如果随机变量X的取值为1的概率为p,那么X取值为0的概率为1-p。如果让上述变量出现n次并把其取值记录下来,就构成一个数据序列,这个序列所服从的分布被称为二项分布。
二项分布检验正是通过检查样本数据的形态来验证总体数据是否符合二项分布,其零假设是样本来自的总体与预设的二项分布没有显著差异。二项分布检验,对于小样本数据应该采用精确检验方法,而对大样本数据则主要采用近似检验方法。
二项分布检验的应用
二项分布检验主要用于判断某种观点是否正确,通常用在基于样品的产品总体合格率检验、或对基于部分学生成绩估算出全体学生及格百分比实施判断。比如,在高考中,总体样本3百万名,在评阅了10000名考生的试卷后,可以做出初步预测:600分以上的学生占10%,那么就可以借助二项分布,检验600分以下的学生占90%的可能性有多大。若这种可能性很大,就可以认为600分以上的学生占10%,否则,则不可以做出此结论。
以产品合格率检验为例,如果需要通过抽样判断产品合格率是否达到90%,其基本思路是:可先假设产品的合格率在90%左右,然后以产品合格作为分割点,把所有样品分为两种状态,判断产品合格率在90%左右的可能性有多大。实施二项分布检验后,若检验合格率>0.05,则接受零假设,认为产品的总体合格率应在90%左右。
偏差拟合度检验
由于偏差度量衡量了模型预测与观察结果的接近程度,我们可能会考虑将其作为给定模型拟合度检验的基础。
虽然我们希望我们的模型预测接近观察到的结果,但即使我们的模型被正确指定,它们也不会相同 – 毕竟,模型给出了观察所遵循的泊松分布的预测平均值。
因此,为了将偏差用作拟合优度检验,我们需要弄清楚,假设我们的模型是正确的,在泊松假设下,我们在预测均值周围观察到的结果中会有多少变化。由于偏差可以作为将当前模型与饱和模型进行比较的轮廓似然比检验得出,因此可能性理论会预测(假设模型被正确指定),偏差遵循卡方分布,自由度等于参数数量的差异。饱和模型可以被视为一个模型,它为每个观察使用不同的参数,因此它具有参数。如果我们提出的模型具有参数,这意味着将偏差与参数的卡方分布进行比较。
在R中执行拟合优度测试
现在看看如何在R中执行拟合优度测试。首先我们将模拟一些简单的数据,具有均匀分布的协变量x和泊松结果y:
set.seed(612312)
n < - 1000
x < - runif(n)
y < - rpois(n,mean)为了使Poisson GLM适合数据,我们只需使用glm函数:
Call:
glm(formula = y ~ x, family = poisson)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.2547 -0.8859 -0.1532 0.6096 3.0254
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.04451 0.05775 -0.771 0.441
x 1.01568 0.08799 11.543 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 1247.7 on 999 degrees of freedom
Residual deviance: 1110.3 on 998 degrees of freedom
AIC: 3140.9
Number of Fisher Scoring iterations: 5这里的偏差被glm函数标记为“残差”,这里是1110.3。有1000个观测值,我们的模型有两个参数,因此自由度为998,由R作为残差df给出。为了计算偏差拟合度检验的p值,我们简单地计算998自由度上卡方分布的偏差值右侧的概率:
pchisq(mod $ deviance,df = mod $ df.residual,lower.tail = FALSE)
[1] 0.00733294零假设是我们的模型被正确指定,我们有强有力的证据来拒绝这个假设。因此,我们有充分的证据表明我们的模型非常适合。
通过仿真检验泊松回归拟合检验的偏差优度
为了研究测试的性能,我们进行了一个小的模拟研究。我们将使用与以前相同的数据生成机制生成10,000个数据集。对于每一个,我们将拟合(正确的)泊松模型,并收集拟合p值的偏差良好性。然后我们将看到它小于0.05的次数:
nSim <- 10000
pvalues <- array(0, dim=nSim)
for (i in 1:nSim) {
n <- 1000
x <- runif(n)
mean <- exp(x)
y <- rpois(n,mean)
mod <- glm(y~x, family=poisson)
pvalues[i] <- pchisq(mod$ , df=mod$df. , lower.tail= )
}
mean(1*(pvalues<0.05))最后一行创建一个向量,其中如果p值小于0.05,则每个元素为1,否则为零,然后使用mean()计算这些元素的比例。当我运行这个时,我得到了0.9437,这意味着偏差测试错误地表明我们的模型在94%的情况下被错误地指定
为了在平均值较大时查看情况是否发生变化,让我们修改模拟。我们现在将生成具有泊松均值的数据,其结果为20到55:
nSim < - 10000
pvalues < - array(0,dim = nSim)
for(i in 1:nSim){
n < - 1000
x < - runif(n)
< - exp(3 + x)
y < - rpois(n,mean)
mod < - glm(y~x,family = poisson)
pvalues [i] < - pchisq(mod $ ,df = mod $ df. ,lower.tail = FALSE)
}
现在,显着偏差测试的比例降低到0.0635,更接近标称的5%1类错误率。
结论
上面显然是一个非常有限的模拟研究,但我对结果的看法是,虽然偏差可能表明泊松模型是否适合,但我们应该对使用由此产生的p值有些警惕。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析
视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析 Python谷歌商店Google Play APP评分预测:LASSO、多元线性回归、岭回归模型对比研究
Python谷歌商店Google Play APP评分预测:LASSO、多元线性回归、岭回归模型对比研究 Python+AI提示词出租车出行轨迹:梯度提升GBR、KNN、LR回归、随机森林融合预测及贝叶斯概率异常检测研究
Python+AI提示词出租车出行轨迹:梯度提升GBR、KNN、LR回归、随机森林融合预测及贝叶斯概率异常检测研究 Python对Airbnb北京、上海链家租房数据用逻辑回归LR、决策树、岭回归、Lasso、随机森林、XGBoost、神经网络kmeans聚类分析市场影响因素|数据分享
Python对Airbnb北京、上海链家租房数据用逻辑回归LR、决策树、岭回归、Lasso、随机森林、XGBoost、神经网络kmeans聚类分析市场影响因素|数据分享


