每一个动态现象都可以用一个潜过程(Λ(t)来描述,这个潜过程在连续的时间t内演化。
当对重复测量的标志变量进行建模时,我们通常不会把它看成是一个有误差测量的潜过程。然而,这正是混合模型理论所做的基本假设。
可下载资源
模型背景
潜过程混合模型利用这个框架将线性混合模型理论扩展到任何类型的结果(有序、二元、连续、类别与任何分布)。
即固定效应模型(fixed effects model),随机效应模型(random effects model),混合效应模型(mixed effects model)。
所谓的固定、随机、混合,主要是针对分组变量而言的。
固定效应模型,表示你打算比较的就是你现在选中的这几组。例如,我想比较3种药物的疗效,我的目的就是为了比较这三种药的差别,不想往外推广。这三种药不是从很多种药中抽样出来的,不想推广到其他的药物,结论仅限于这三种药。“固定”的含义正在于此,这三种药是固定的,不是随机选择的。
随机效应模型,表示你打算比较的不仅是你的设计中的这几组,而是想通过对这几组的比较,推广到他们所能代表的总体中去。例如,你想知道是否名牌大学的就业率高于普通大学,你选择了北大、清华、北京工商大学、北京科技大学4所学校进行比较,你的目的不是为了比较这4所学校之间的就业率差异,而是为了说明他们所代表的名牌和普通大学之间的差异。你的结论不会仅限于这4所大学,而是要推广到名牌和普通这样的一个更广泛的范围。“随机”的含义就在于此,这4所学校是从名牌和普通大学中随机挑选出来的。混合效应模型就比较好理解了,就是既有固定的因素,也有随机的因素。
一般来说,只有固定效应模型,才有必要进行两两比较,随机效应模型没有必要进行两两比较,因为研究的目的不是为了比较随机选中的这些组别。
固定效应和随机效应的选择是大家做面板数据常常要遇到的问题,一个常见的方法是做huasman检验,即先估计一个随机效应,然后做检验,如果拒绝零假设,则可以使用固定效应,反之如果接受零假设,则使用随机效应。但这种方法往往得到事与愿违的结果。另一个想法是在建立模型前根据数据性质确定使用那种模型,比如数据是从总体中抽样得到的,则可以使用随机效应,比如从N个家庭中抽出了M个样本,则由于存在随机抽样,则建议使用随机效应,反之如果数据是总体数据,比如31个省市的Gdp,则不存在随机抽样问题,可以使用固定效应。同时,从估计自由度角度看,由于固定效应模型要估计每个截面的参数,因此随机效应比固定效应有较大的自由度.
固定效应模型
固定效应模型(fixed effects model)的应用前提是假定全部研究结果的方向与效应大小基本相同,即各独立研究的结果趋于一致,一致性检验差异无显著性。因此固定效应模型适用于各独立研究间无差异,或差异较小的研究。
固定效应模型是指实验结果只想比较每一自变项之特定类目或类别间的差异及其与其他自变项之特定类目或类别间交互作用效果,而不想依此推论到同一自变项未包含在内的其他类目或类别的实验设计。例如:研究者想知道教师的认知类型在不同教学方法情境中,对儿童学习数学的效果有何不同,其中教师和学生的认知类型,均指场地依赖型和场地独立型,而不同的教学方法,则指启发式、讲演式、编序式。当实验结束时,研究者仅就两种类型间的交互作用效果及类型间的差异进行说明,而未推论到其他认知类型,或第四种教学方法。象此种实验研究模式,即称为固定效果模式。(mixed effect model)。
随机效应模型 random effects models
随机效应模型(random effects models)是经典的线性模型的一种推广,就是把原来(固定)的回归系数看作是随机变量,一般都是假设是来自正态分布。如果模型里一部分系数是随机的,另外一些是固定的,一般就叫做混合模型(mixed models)。
虽然定义很简单,对线性混合模型的研究与应用也已经比较成熟了,但是如果从不同的侧面来看,可以把很多的统计思想方法综合联系起来。概括地来说,这个模型是频率派和贝叶斯模型的结合,是经典的参数统计到高维数据分析的先驱,是拟合具有一定相关结构的观测的典型工具。
随机效应最直观的用处就是把固定效应推广到随机效应。注意,这时随机效应是一个群体概念,代表了一个分布的信息 or 特征,而对固定效应而言,我们所做的推断仅限于那几个固定的(未知的)参数。例如,如果要研究一些水稻的品种是否与产量有影响,如果用于分析的品种是从一个很大的品种集合里随机选取的,那么这时用随机效应模型分析就可以推断所有品种构成的整体的一些信息。这里,就体现了经典的频率派的思想-任何样本都来源于一个无限的群体(population)。
同时,引入随机效应就可以使个体观测之间就有一定的相关性,所以就可以用来拟合非独立观测的数据。经典的就有重复观测的数据,多时间点的记录等等,很多时候就叫做纵向数据(longitudinal data),已经成为很大的一个统计分支。
潜类别混合模型
潜类别混合模型在Proust-Lima等人中介绍(2006 https://doi.org/10.1111/j.1541-0420.2006.00573.x 和2013 https://doi.org/10.1111/bmsp.12000 )。
使用线性混合模型根据时间对定义为潜过程感兴趣的变量进行建模:
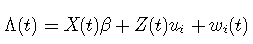
其中:
- X(t) 和Z(t) 是协变量的向量(Z(t) ;
- β 是固定效应(即总体均值效应);
- ui 是随机效应(即个体效应);它们根据具有协方差矩阵B 的零均值多元正态分布进行分布;
- (wi(t)) 是高斯过程,可以添加到模型中以来放宽对象内部相关结构。
同时在观察方程中定义了感兴趣的潜过程标志变量Yij (针对对象i和场合j)的观察之间的关系:
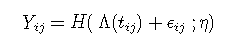
其中
- tij 是主题i 和场合j 的测量时间;
- ϵij 是一个独立的零均值高斯误差;
- H 是链接函数,可将潜过程转换为比例和度量。
使用了不同的参数族。 当标志变量为连续时,H-1 是递增单调函数的参数族,其中:
- 线性变换:这简化为线性混合模型(2个参数)
- Beta累积分布族重新调整(4个参数)
当标志变量是离散类别(二元或有序的)时: H是阈值函数,即Y的每个级别对应于要估计Λ(tij)+ ϵij区间的边界。
可识别性
与任何潜变量模型一样,必须定义潜变量的度量。在lcmm中,误差的方差为1,平均截距(在β中)为0。
示例
在本文中,lcmm 通过研究年龄65岁左右男性的抑郁症状(由CES-D量表测量)的线性轨迹来说明潜过程混合模型 。包括截距和age65的相关随机效应。
考虑的模型:
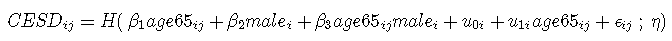
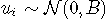 ,
,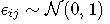
固定效应部分 是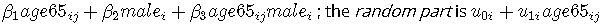
估计不同连续链接函数的模型H
我们使用65岁左右的年龄变量进行中心化,并以十年为单位。
潜过程混合模型可以用不同的链接函数进行拟合,如下所示。这是用参数链接来完成的。
线性链接函数
定义线性链接函数时,模型将简化为标准线性混合模型。默认情况下具有线性链接函数:
lcmm(CESD ~ age65*male, random=~ age65 #链接=线性它与hlme的模型完全相同。与hlme对象的唯一区别是截距和残差标准误差的参数化。
hlme(CESD ~ age65*male, random=~ age65 #链接=线性对数似然相同,但估计参数β不在同一范围内
loglik
[1] -7056.652

非线性链接函数1:Beta累积分布函数Beta分布的重标累积分布函数(CDF)提供了标志变量与其基本潜伏过程之间的凹、凸或sigmoïd变换。
lcmm( random=~ age65, link='beta')非线性链接函数2:二次I样条二次I样条族近似于连续增加的链接函数。它涉及在标志变量范围内分布的节点。默认情况下,使用位于标志变量范围内的5个等距结:
lcmm(random=~ age65, subject='ID', link='splines')可以指定结的数量及其位置。首先输入节点的数目,接着 ,再指定位置 equi, quant 或 manual 用于分别等距节点,在标志变量分布分位数或内部结在参数intnodes手动输入。例如, 7-equi-splines 意味着具有7个等距节点,6-quant-splines I样条, 意味着具有6个节点的I样条,其位于标志变量分布的分位数处。
随时关注您喜欢的主题
例如,在分位数处有5个结:
lcmm(link='5-quant-splines')选择最佳模型
要选择最合适的链接函数,可以比较这些不同的模型。通常,这可以通过使用AIC 或 UACV等顺着根据拟合优度对模型进行比较来实现 。
AIC(每个模型的输出中都有UACV):
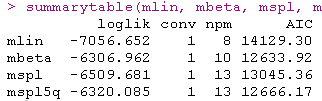
在这种情况下,根据AIC标准,由I-splines和5个分位数结点链接函数的模型提供了最佳拟合度。可以在图中比较不同的估计链接函数:
plot(mli, which="linkfunction",xlab="潜过程")
legend(x="topleft", legend=c("线性", "beta","样条曲线 (5个等距结点)","样条曲线(5个分位数结点)"))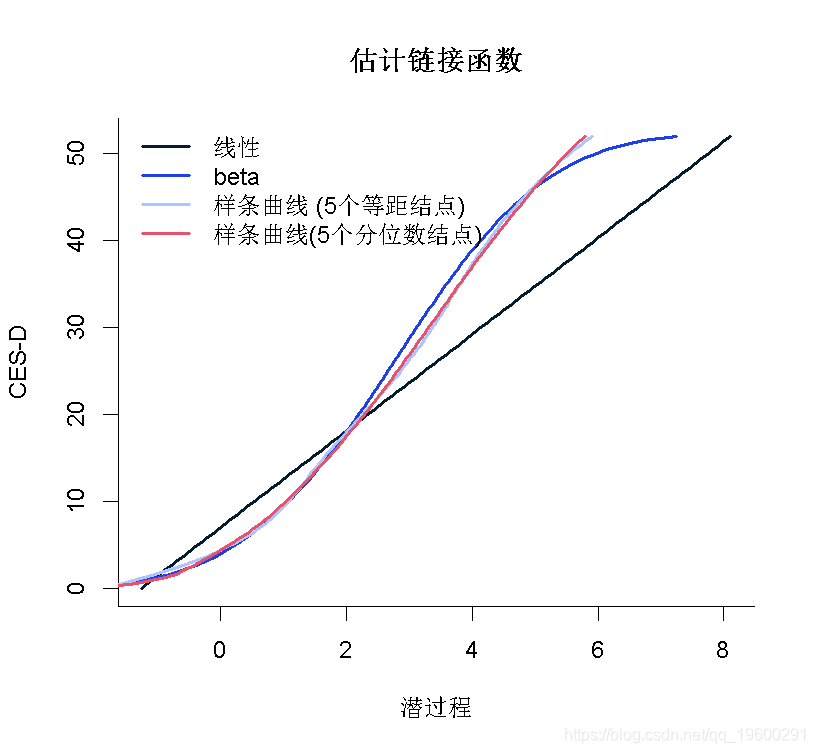
我们看到2个样条曲线转换非常接近。线性模型似乎不合适,如线性曲线和样条曲线之间的差值所示。Beta转换仅在潜过程的高值时才与样条曲线不同。变换的置信带可以通过蒙特卡洛方法获得:
predict(mspl5q,ndraws=2000)
legend(legend=c("95% 置信带","分位数样条"),lty=c(2,NA))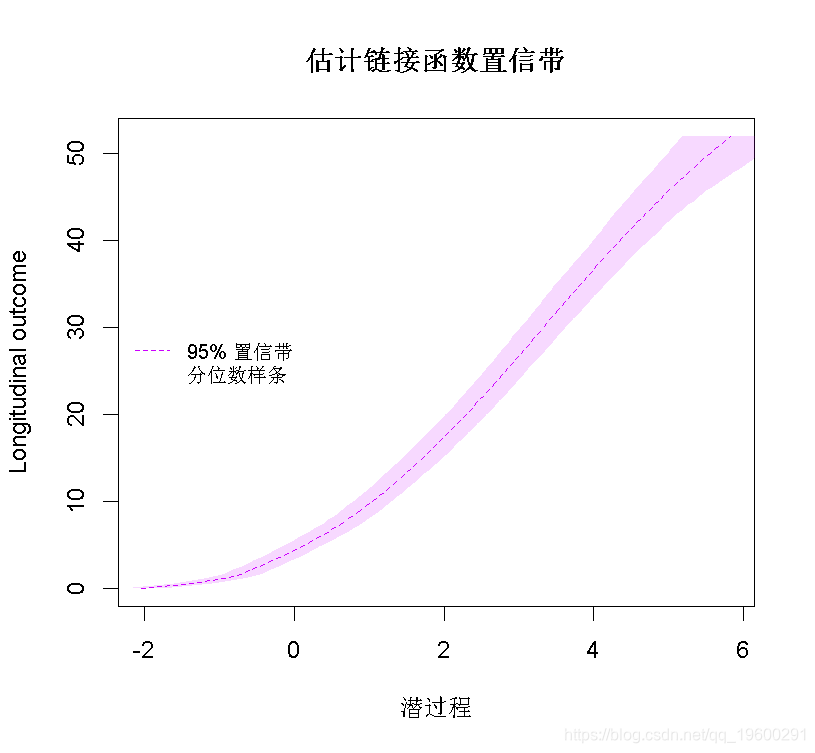
注意,该模型成为累积概率混合模型。这里是一个使用HIER变量(4级)的例子,因为考虑到0-52的范围(例如52个阈值参数),CESD的阈值链接函数会涉及太多参数。
用离散链接函数H估计模型
有时,对于仅具有有限数量级别的标志变量,连续链接函数不合适,并且必须处理标志变量的有序性质。lcmm函数通过考虑阈值链接函数来处理这种情况。然而,我们必须知道,带有阈值链接函数的模型的数值复杂性要重要得多(由于对随机效应分布进行了数值积分)。在拟合这个模型时,必须牢记这一点,随机效应的数量要严谨地选择。
lcmm(HIER ~ age65*male, link='thresholds')拟合后的输出
概要
该模型的摘要包括收敛性,拟合标准的优度和估计的参数。

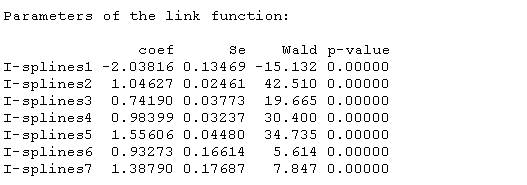
根据协变量的分布预测的轨迹图,可以根据因变量的比例并根据协变量的分布来计算预测的轨迹:
predict(msp, newdata=datnew, var.time="age"然后绘制:
plot(women,xlab="年龄")
plot(men, add=TRUE)
legend(legend=c("女性","男性", "95% 置信区间", "95% 置信区间"))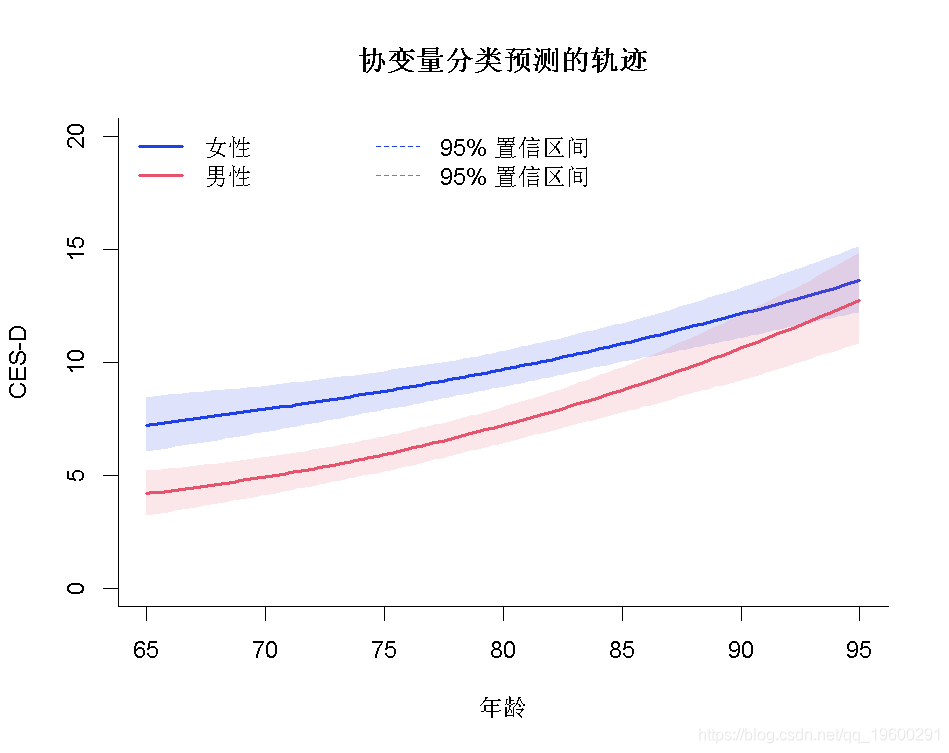
拟合优度1:残差图
特定的残差(右下方面板中的qqplot)应为高斯分布。
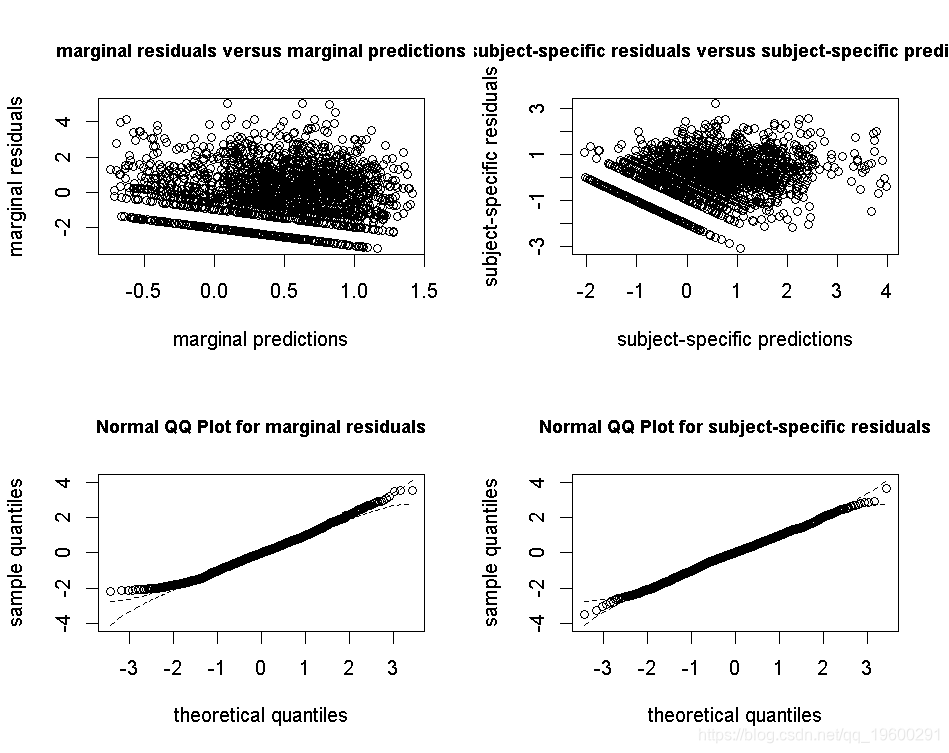
拟合优度2:预测与观察图
可以根据年龄绘制平均预测和观察值。请注意,预测和观察是在潜过程的范围内(观察是通过估计的链接函数进行转换的):
plot( var.time="age65", xlab="(年龄-65)/10", break.times=8, ylab="潜过程")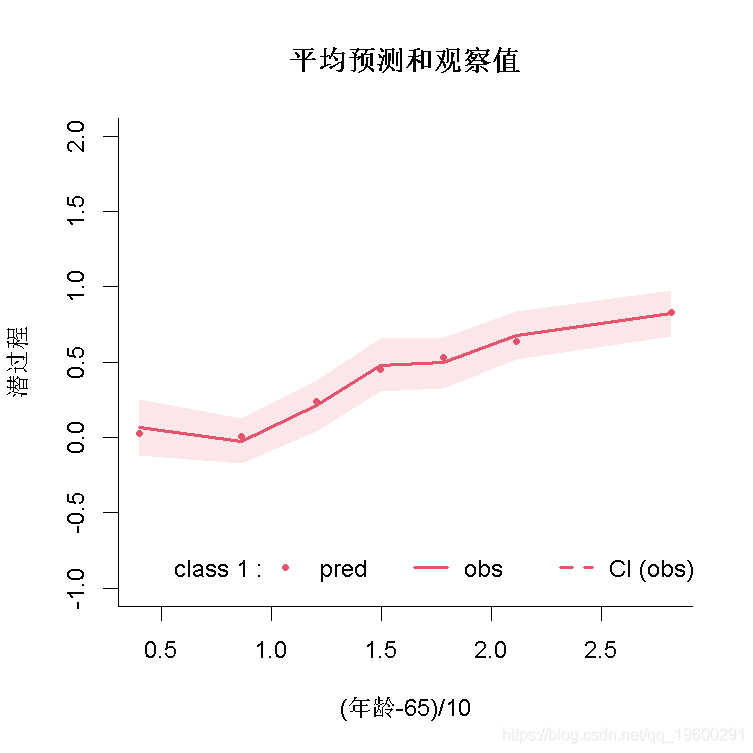
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析
视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析 高维变量选择专题|R、Python用HOLP、Lasso、SCAD、PCR、ElasticNet实例合集分析企业财务、糖尿病、基因数据
高维变量选择专题|R、Python用HOLP、Lasso、SCAD、PCR、ElasticNet实例合集分析企业财务、糖尿病、基因数据 R软件线性模型与lmer混合效应模型对生态学龙类智力测试数据层级结构应用
R软件线性模型与lmer混合效应模型对生态学龙类智力测试数据层级结构应用 R语言LCMM多维度潜在类别模型流行病学研究:LCA、MM方法分析纵向数据
R语言LCMM多维度潜在类别模型流行病学研究:LCA、MM方法分析纵向数据
