资产价格具有随时间变化的波动性（逐日收益率的方差）。
在某些时期，收益率是高度变化的，而在其他时期则非常平稳。
视频
随机波动率SV模型原理和Python对标普SP500股票指数时间序列波动性预测
最近我们被客户要求撰写关于随机波动率的研究报告，包括一些图形和统计输出。
随机波动率模型用一个潜在的波动率变量来模拟这种情况，该变量被建模为随机过程。下面的模型与 No-U-Turn Sampler 论文中描述的模型相似，Hoffman (2011) p21。
×
隐含波动率是BSM框架下每个期权报价倒推出的唯一常数解。对于不同的到期时间Tm，不同行权价格Kn，对应着不同的隐含波动率IV（m,n），它们构成了波动率曲面。问题转换成如何解释曲面。局部波动率倾向于在空间维度截面展开去拟合波动率微笑，SVI等，高端的可以用Levy中的Mertion’s Jump Diffusion，Kou’s Jump Diffusion, Variance Gamma, Normal Inverse Gaussian等等。 本质上是假设平稳性，去拟合空间截面期权价格使得定价引擎定的价格在某个加权二范数下最小。局部波动率等最重要的满足凸性无蝶式套利，而Levy倾向于寻找拟合分布。随机波动率则把波动率看做随机过程，顾名思义，本质上是扔掉平稳性，HESTON等，在时间维度上寻求拟合。一些广义的非时间其次（非平稳）LEVY过程也有类似效果比如有强理论支持的SATO PROCESSES，寻求时间和空间维度的统一.
这里，r是每日收益率序列，s是潜在的对数波动率过程。
建立模型
首先，我们加载标普500指数的每日收益率。
returns = (pm.get_data("SP500.csv"))
returns\[:5\]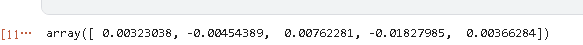
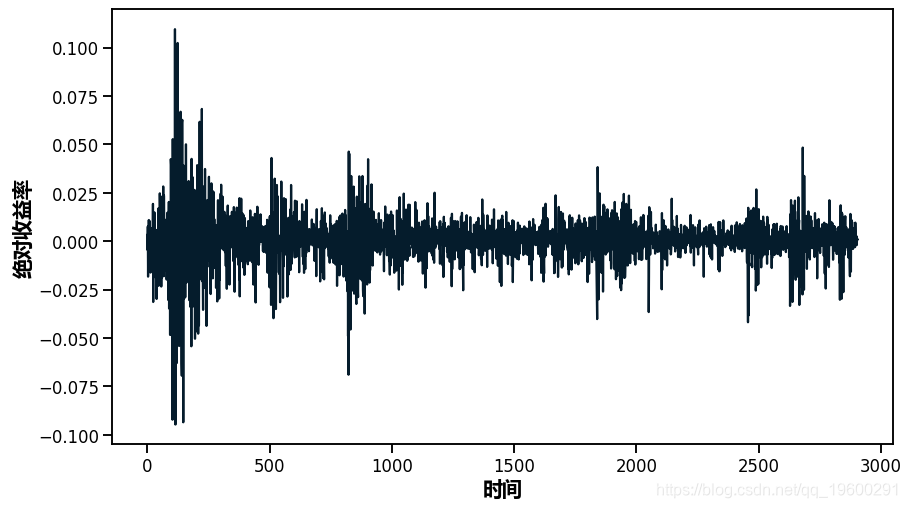
正如你所看到的，波动性似乎随着时间的推移有很大的变化，但集中在某些时间段。在2500-3000个时间点附近，你可以看到2009年的金融风暴。
ax.plot(returns)可下载资源
指定模型。
GaussianRandomWalk('s', hape=len(returns))
nu = Exponential( .1)
r = StudentT( pm.math.exp(-2*s),
obs=returns)拟合模型
对于这个模型，最大后验(_Maximum_ A _Posteriori_,MAP)概率估计具有无限的密度。然而，NUTS给出了正确的后验。
pm.sample(tune=2000
Auto-assigning NUTS sampler...
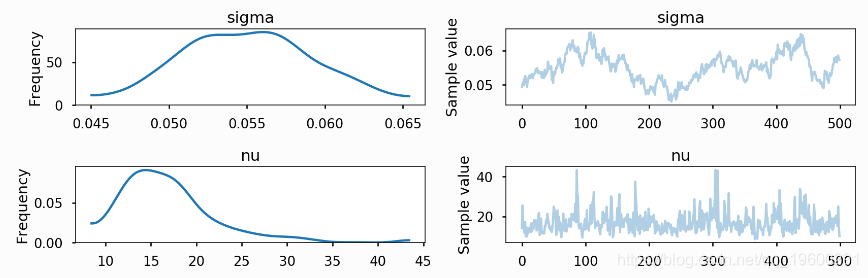
plot(trace\['s'\]);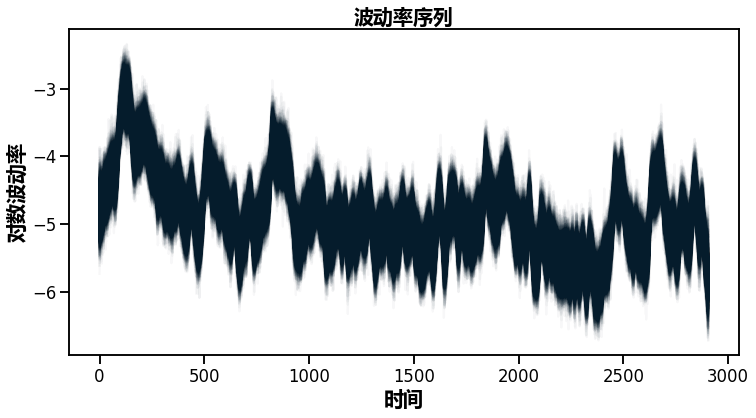
观察一段时间内的收益率，并叠加估计的标准差，我们可以看到该模型是如何拟合一段时间内的波动率的。
随时关注您喜欢的主题
plot(returns)
plot(exp(trace\[s\]);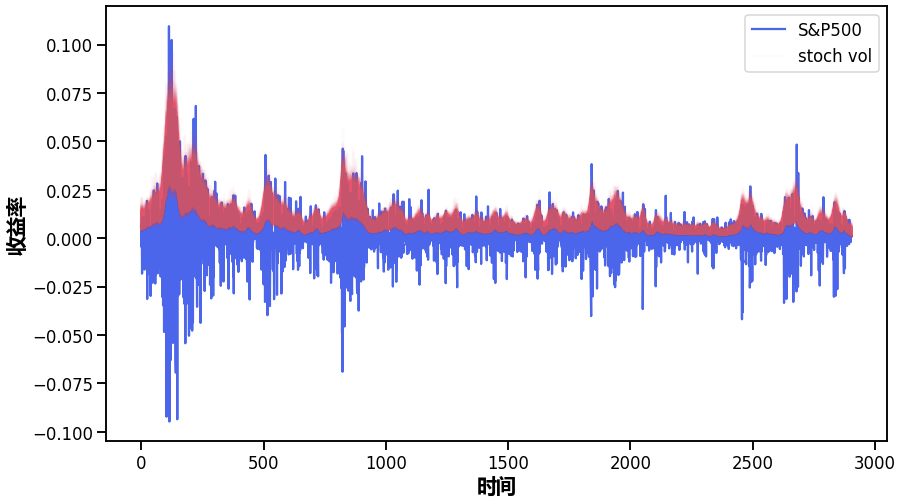
np.exp(trace\[s\])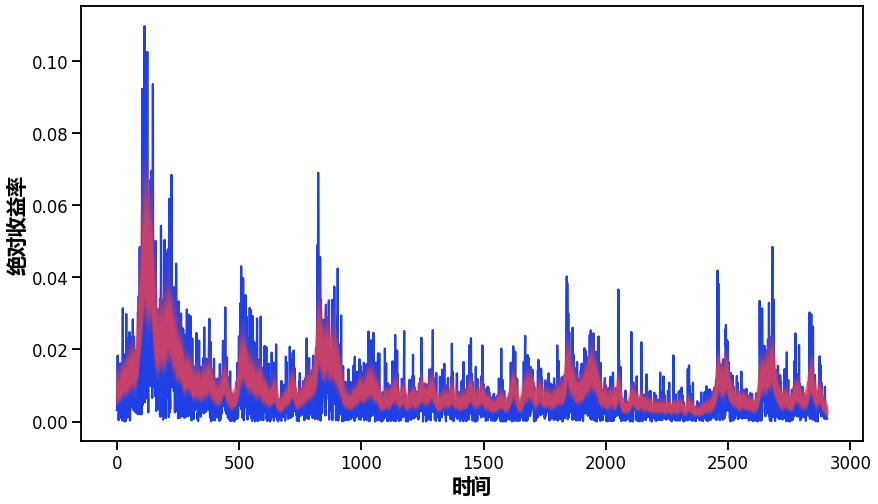
参考文献
- Hoffman & Gelman. (2011). The No-U-Turn Sampler: Adaptively Setting Path Lengths in Hamiltonian Monte Carlo.
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
Python用CEEMDAN-LSTM-VMD金融股价数据预测及SVR、AR、HAR对比可视化
Python注意力机制Attention下CNN-LSTM-ARIMA混合模型预测中国银行股票价格|附数据代码
【梯度提升专题】XGBoost、Adaboost、CatBoost预测合集：抗乳腺癌药物优化、信贷风控、比特币应用|附数据代码
Python用CNN – LSTM、ARIMA、Prophet股票价格预测的研究与分析|附数据代码
