这篇文章展示了自激励阈值自回归SETAR的使用，用于分析经常被客户研究的太阳黑子数据集。
具体而言，研究SETAR模型的估计和预测。
我们在这里考虑原始的太阳黑子序列以匹配ARMA示例，尽管文献中许多来源在建模之前对序列进行变换。
import numpy as np import pandas as pd ......dta.index = pd.Index(sm.......m_range('1700', '2008'))
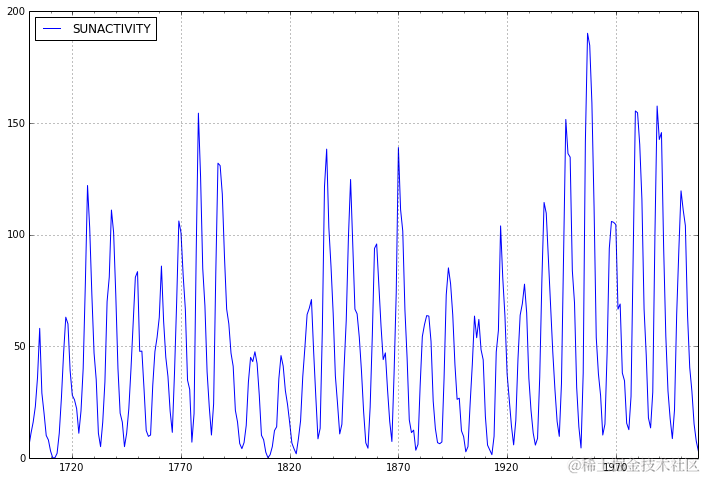
首先，我们将用ARMA对数据进行AR(3)过程拟合。
arma_mod30 = sm.tsa.ARMA(dta, (3,0)).fit()......0.hqic
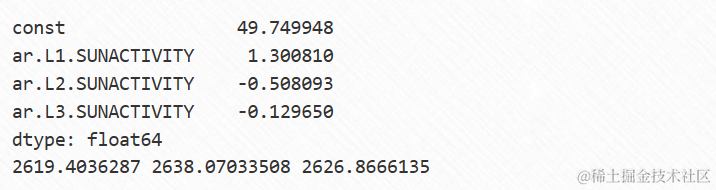
为了测试非线性，可以使用线性AR(3)模型的残差进行BDS检验。
视频
ARIMA时间序列模型原理和R语言ARIMAX预测实现案例
视频
时间序列分析模型 ARIMA-ARCH GARCH模型分析股票价格数据
bds.bds(arm......sid, 3)
这表明可能存在潜在的非线性结构。为了试图捕捉这个结构，我们将对数据拟合SETAR(2)模型，允许两种制度，并且每个制度都是AR(3)过程。在这里，我们没有指定延迟或阈值值，因此它们将从模型中最优选择。
注意：在摘要中，\gamma参数是阈值值。
ser_23 = star......).fit()
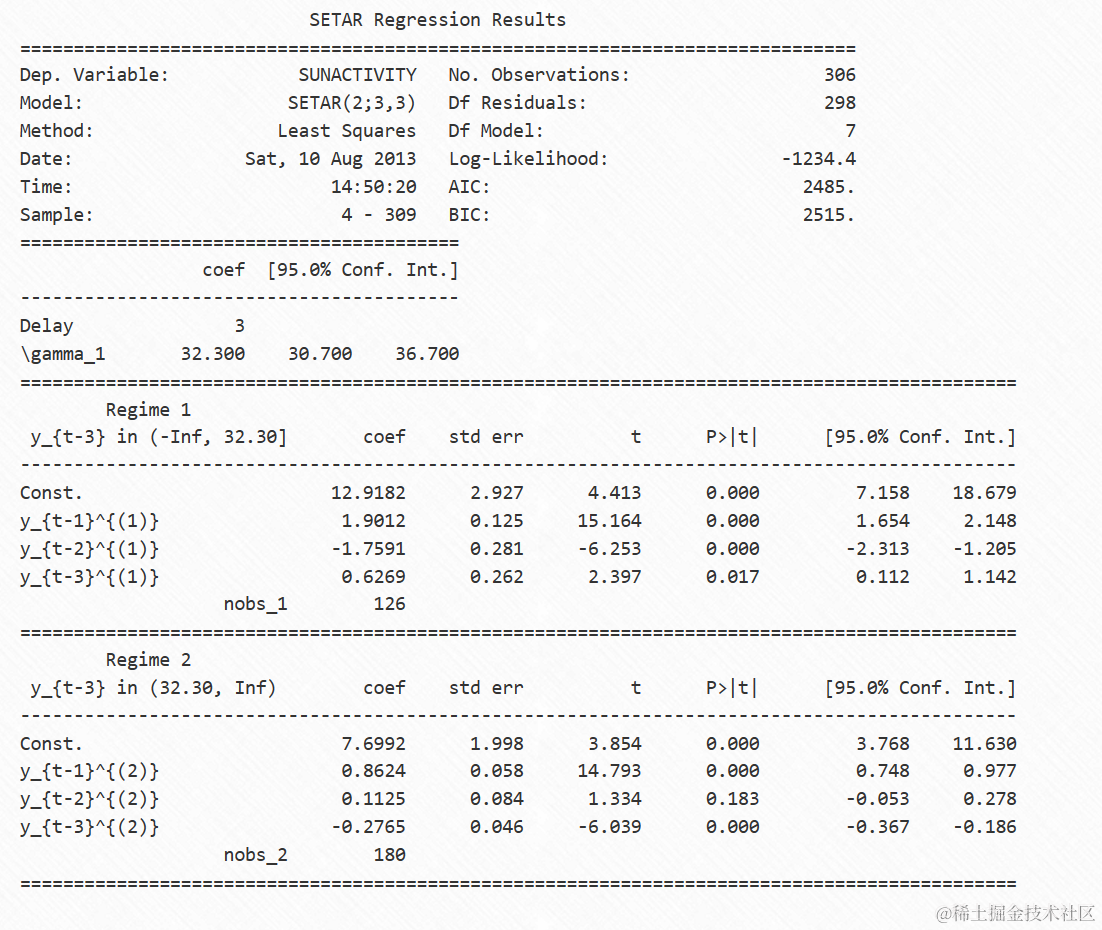
AIC和BIC准则更喜欢SETAR模型而不是AR模型。
注意：这是一个自助法检验，所以在改进之前速度可能会比较慢。
f_sat, pae,bsf_tas = stoest()
零假设是SETAR(1)，因此我们可以拒绝它，选择SETAR(2)作为备择假设。
不过需要注意的是，order_test()的默认假设是存在异方差性，这在这里可能是不合理的。
f_stat_h, pvalue_h, bs_f_stats_h = ......g')
print pvalue
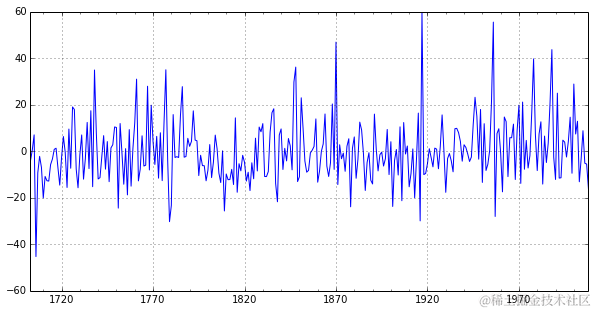
需要注意，在考虑时序残差时，BDS检验仍然拒绝原假设，尽管比AR(3)模型的拒绝程度更小。我们可以查看残差图，看看误差是否具有零均值，但可能不具有同方差性。
print bds.bds(setar_mod23.resid, 3)
setar_mod23.resid.plot(figsize=(10,5));
随时关注您喜欢的主题
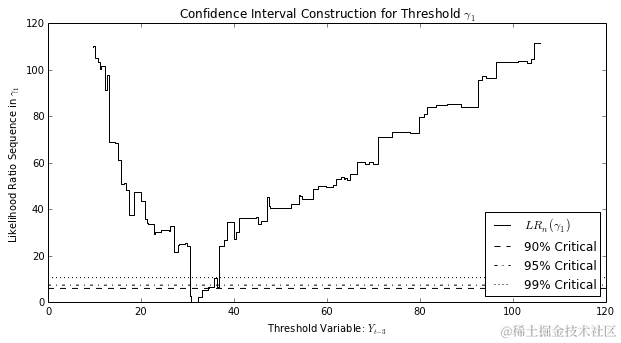
相对于ARMA模型，这里估计了两种新类型的参数。延迟参数和阈值。延迟参数选择要使用作为阈值变量的过程滞后，并且阈值指示将数据点分隔为（此处为两个）状态的阈值变量的哪些值。
似然比统计量小于临界值的替代阈值包含在置信集中，置信区间的下限和上限分别是置信集中最小和最大的阈值。
setarmd23.plo......ght=5);
我们可以查看样本内动态预测和样本外预测。
predit_am_mo30 = arma_mod30.predict('1990', '2012', dynamic=True)
ax = dta.ix['1950':].pot(igsze=(12,8))......
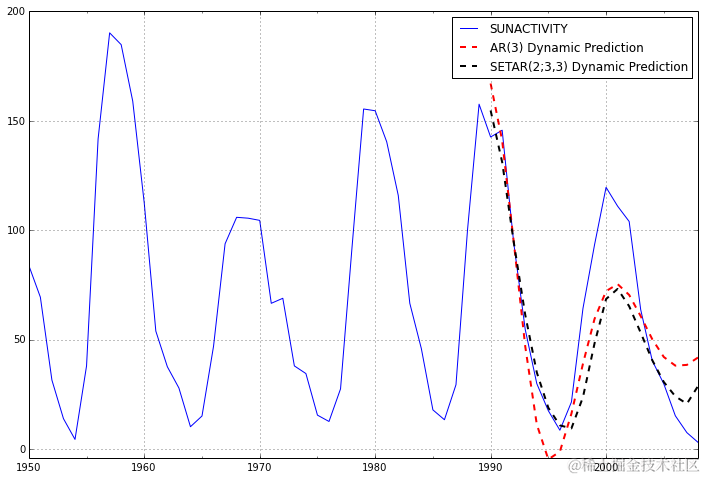
看起来，SETAR模型的动态预测能够稍微更好地跟踪观察到的数据点，而不是AR(3)模型。我们可以通过均方根预测误差进行比较，并看到SETAR表现略好一些。
def rsf(y, yhat):
return (y.sb(yhat**2).man()
prnt 'AR(3): ', rse(dta.SNACTIVI......od23)
然而，如果扩展预测窗口，则明显SETAR模型是唯一一个适合数据形状的模型，因为数据是循环的。
preict_am_mo30_long = ama_md30.predict('1960', '2012', dynamic=True)......
ax.legend();
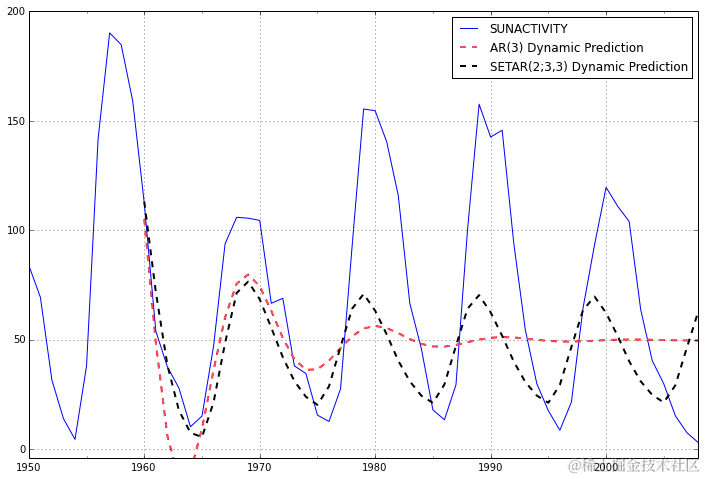
print 'AR(3): ', rmsfe(dta.S......ong)
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
【视频】R语言支持向量回归SVR预测水位实例讲解|附代码数据
数据分享|R语言Python机器学习预测4案例合集：众筹平台、机票折扣、糖尿病患者、员工满意度
R语言神经网络模型金融应用预测上证指数时间序列可视化
R语言用随机森林模型的酒店收入和产量预测误差分析
