在数据科学的领域中，我们常常会遇到需要处理复杂关系的数据。
在众多的数据分析方法中，样条拟合是一种非常有效的处理数据非线性关系的手段。
本专题合集围绕如何使用PyMC软件，对樱花花期数据进行样条拟合分析展开了一系列深入的探讨。本专题合集涵盖了从数据的获取、清洗，到模型的构建、拟合，再到模型结果的分析和新数据预测等多个关键环节。
数据方面，我们使用了记录每年樱花树开花天数（“一年中的天数”即doy）和年份（year）的樱花花期数据。在数据处理时，为了方便，我们剔除了缺失开花天数数据的年份（但一般来说，这并不是处理缺失数据的好方法）。
在模型构建部分，我们构建了一个基于正态分布的模型来描述樱花花期天数的变化。模型中，开花天数D被建模为均值为μ、标准差为σ的正态分布，而均值μ又是由截距a和由基函数B与模型参数w的乘积组成的线性模型。
在模型拟合完成后，我们对模型的后验抽样结果进行了详细分析，包括参数估计、模型预测等方面。最后，我们还探讨了如何使用该模型对新数据进行预测，尽管样条拟合方法在处理超出原始数据范围的数据时存在一定的局限性。
本文代码数据已分享在交流社群，阅读原文进群和500+行业人士共同交流和成长。希望本专题合集的内容能够为数据科学领域的从业者和爱好者提供有价值的参考，帮助大家更好地理解和应用样条拟合方法，解决实际数据分析中的问题。
数据准备
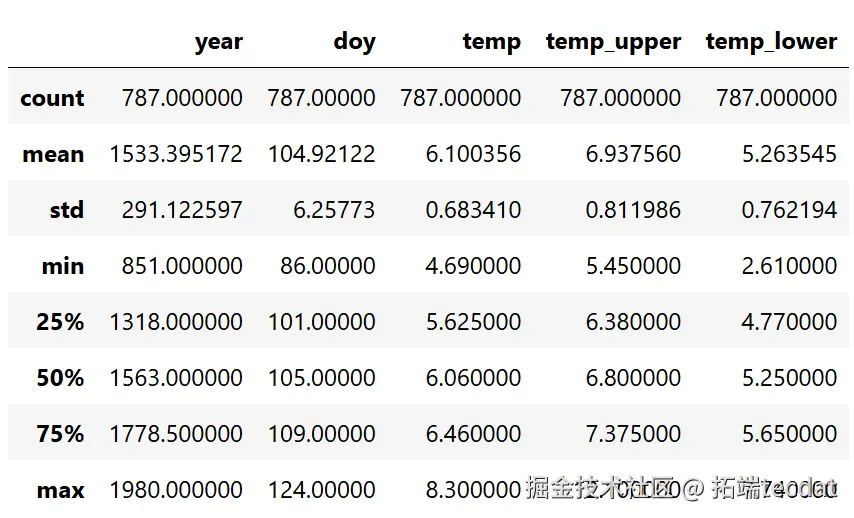
- AI提示词：使用Python语言，通过pandas库读取存储樱花花期数据的CSV文件，若文件不存在则从指定位置读取，然后对数据进行缺失值处理并查看数据基本描述信息
from pathlb iport Path import padas as pd try cherry_blossom_ata = pd.read_csv(Pth(".", "data"cm.csv"), sep=";")经过缺失值处理后，数据集中包含了827个年份的樱花开花天数信息。从数据的可视化散点图中可以看出，虽然每年的开花天数存在很大的变化，但随着时间的推移，开花天数呈现出一定的非线性趋势。
想了解更多关于模型定制、辅导的信息？
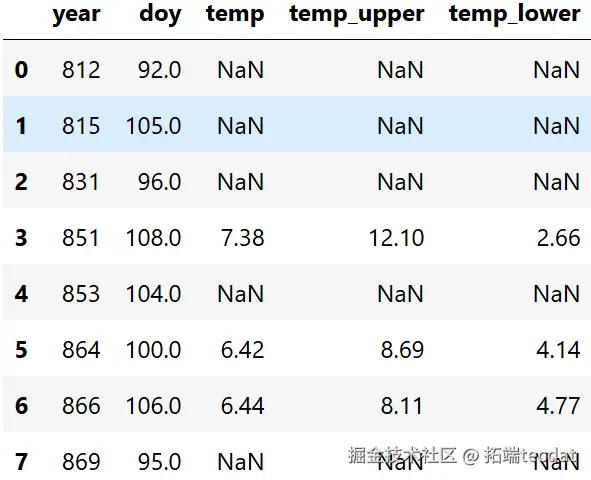
print(cherry_blossom_data.head(n=10))
视频
非线性模型原理与R语言多项式回归、局部平滑样条、 广义相加模型GAM分析
视频
贝叶斯推断线性回归与R语言预测工人工资数据
模型构建
- AI提示词：使用PyMC库构建一个基于正态分布的模型，定义模型的参数，包括截距a、参数w、标准差sigma等，并确定它们的先验分布
COORDS = {"splines": np.arange(B.shape[1])}
with pm.Model
在这个模型中，我们使用了15个节点将年份数据分成了16个部分，并使用patsy库创建了三次样条基矩阵B。
B = dmatrix(
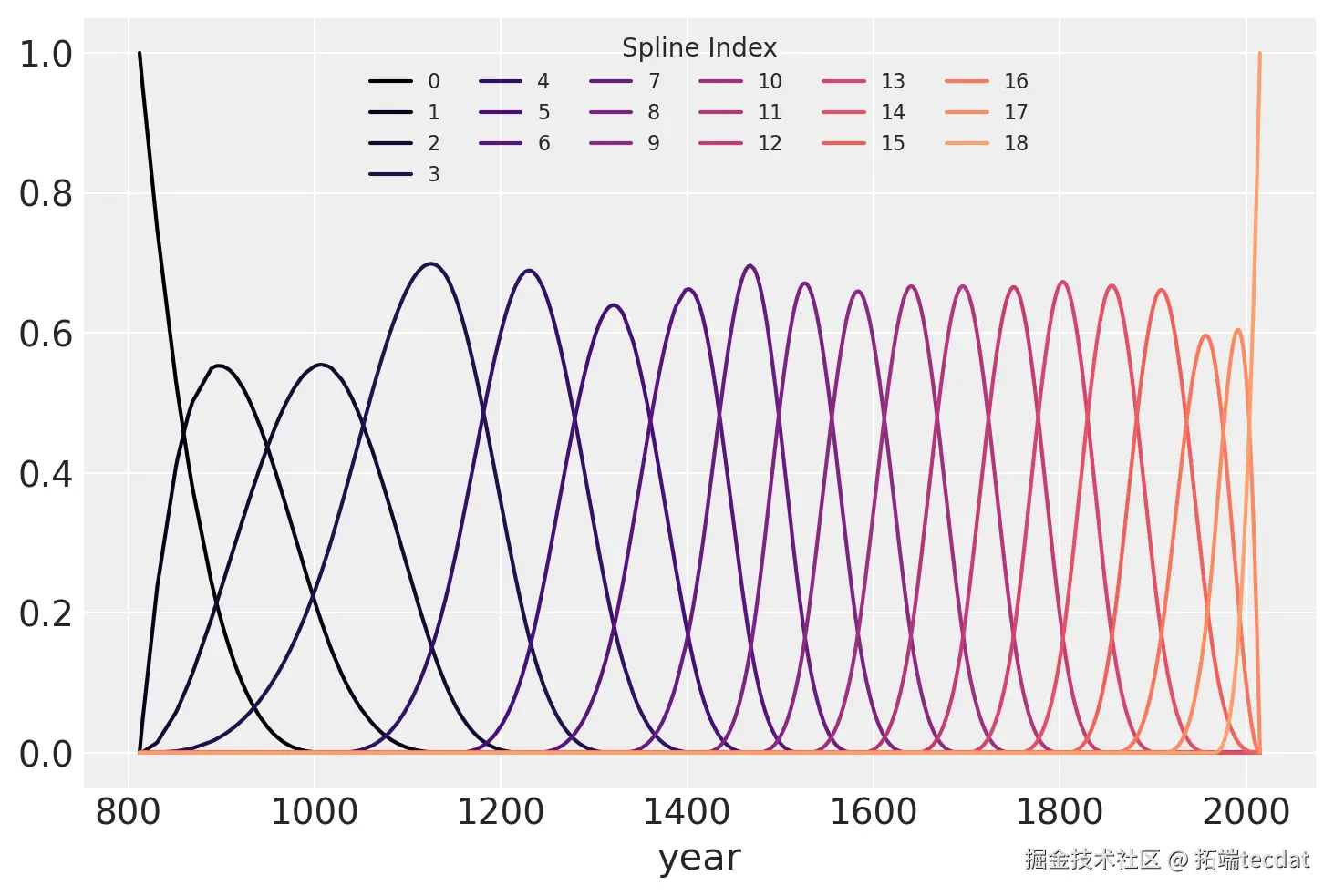
下面是样条基的绘图，显示了样条每一段的“域”。每条曲线的高度表示相应的模型协变量（每个样条区域一个）对该区域模型推断的影响程度。重叠区域表示节点，显示了从一个区域到下一个区域的平滑过渡是如何形成的。
color = plt.cm.magma(np.linspace(0, 0.80, len(spline_df.spline_i.unique())))
模型拟合
- AI提示词：使用PyMC库对构建好的模型进行抽样，获取先验预测值、后验预测值，设置抽样的相关参数如抽样次数、调优次数、链的数量等
idata = pm.sample_prior_predictive()
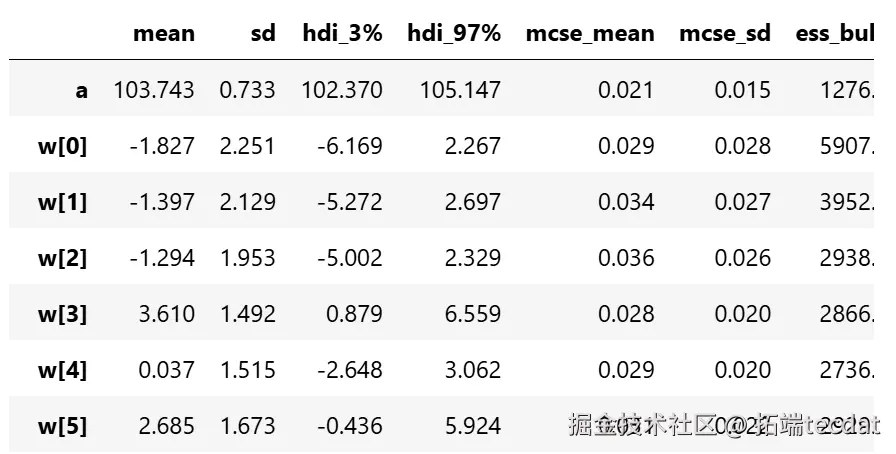
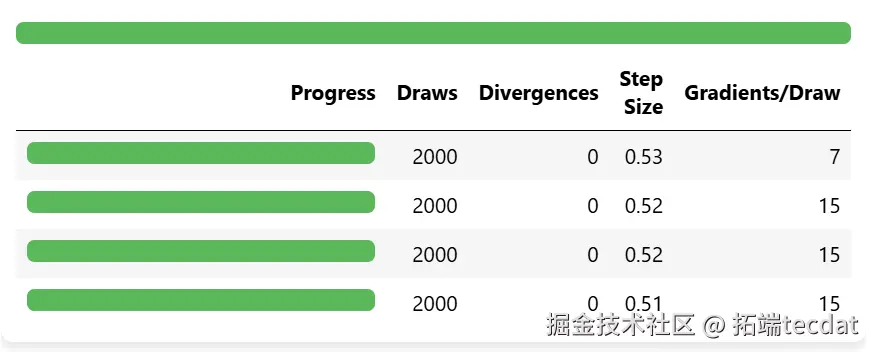
通过模型拟合，我们可以得到模型参数的后验分布，并对模型的收敛性进行检查。
从参数估计的结果来看，截距a和标准差σ的后验分布比较窄，而参数w的后验分布较宽。这可能是因为估计a和σ时使用了所有的数据点，而估计每个w值时只使用了部分数据。
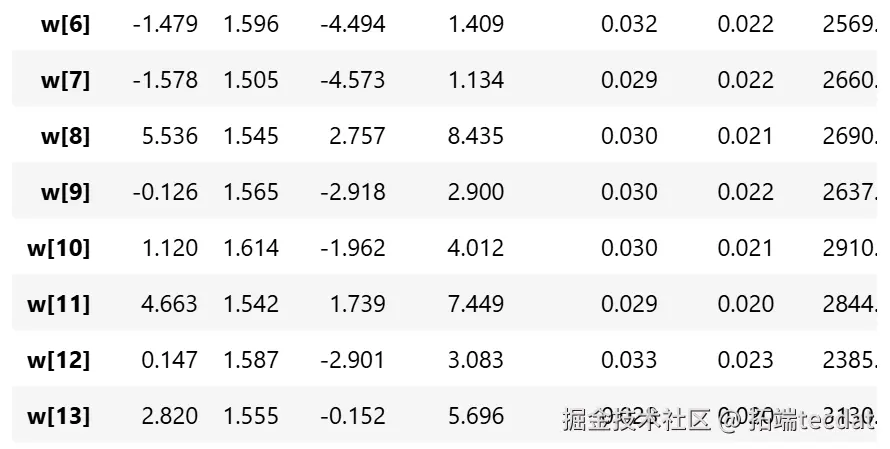
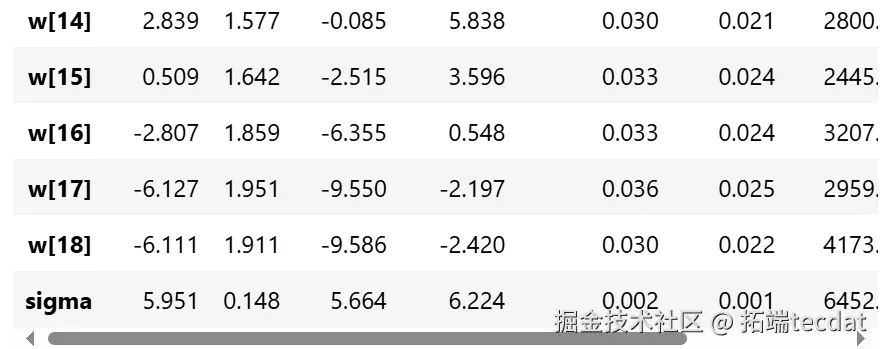
2. AI提示词：使用arviz库绘制模型参数a、w、sigma的迹图，观察参数的收敛情况和分布特征
az.plot_trace(idata, var_names=["a", "w", "sigma"]);
迹图显示模型的链已经收敛，并且没有明显的趋势，进一步表明模型已经很好地从后验分布中抽样。
\
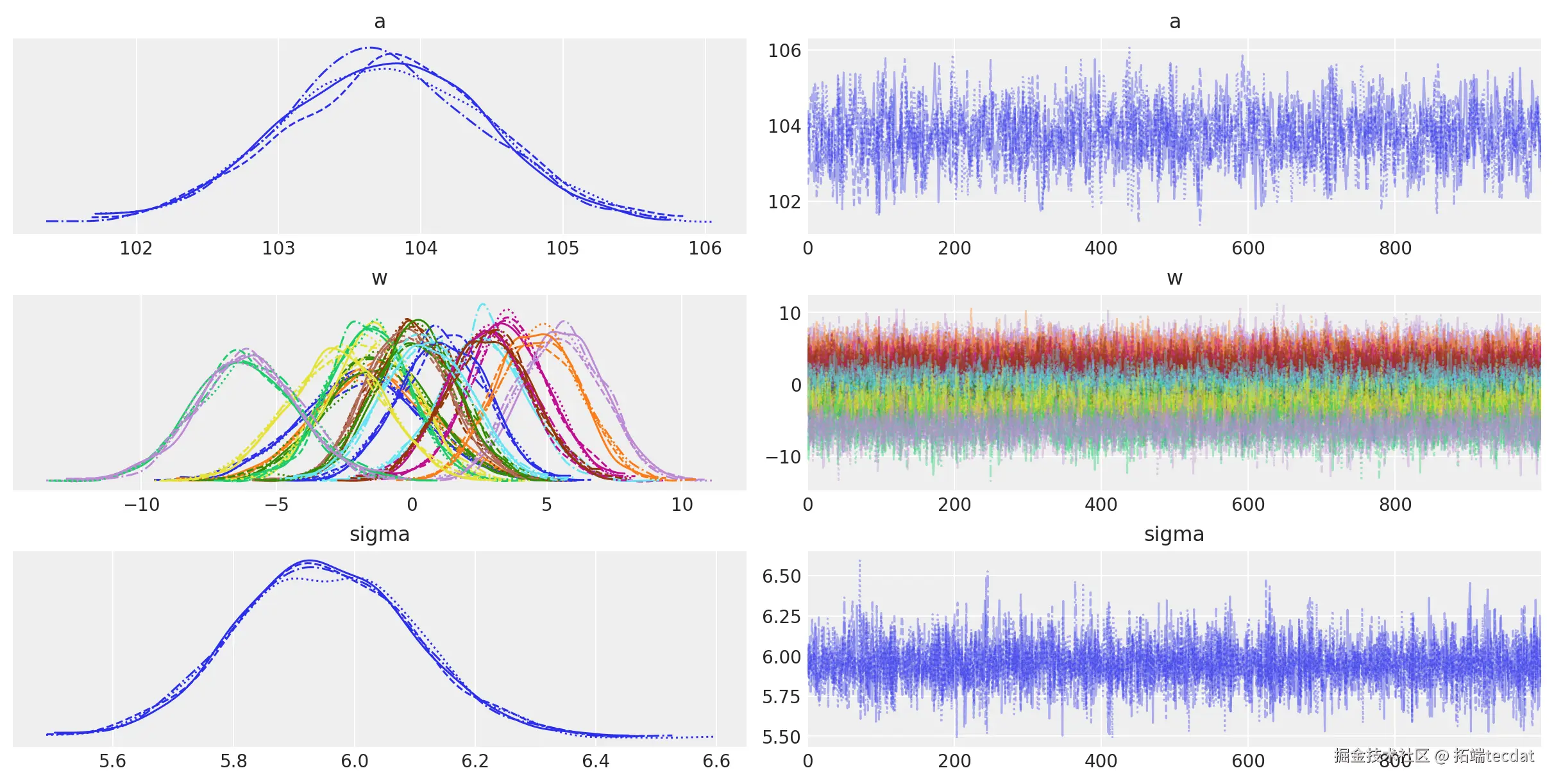
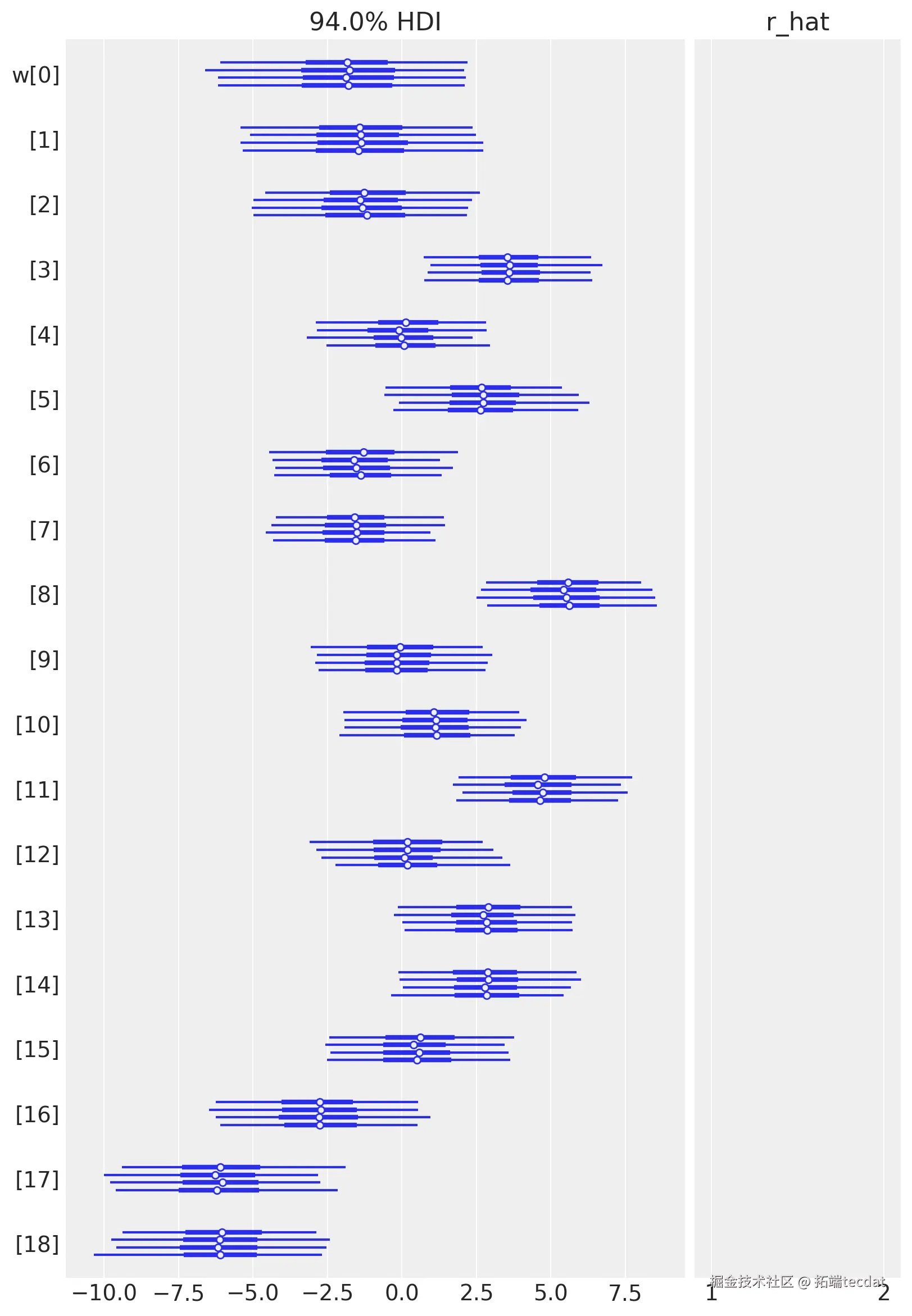
随时关注您喜欢的主题
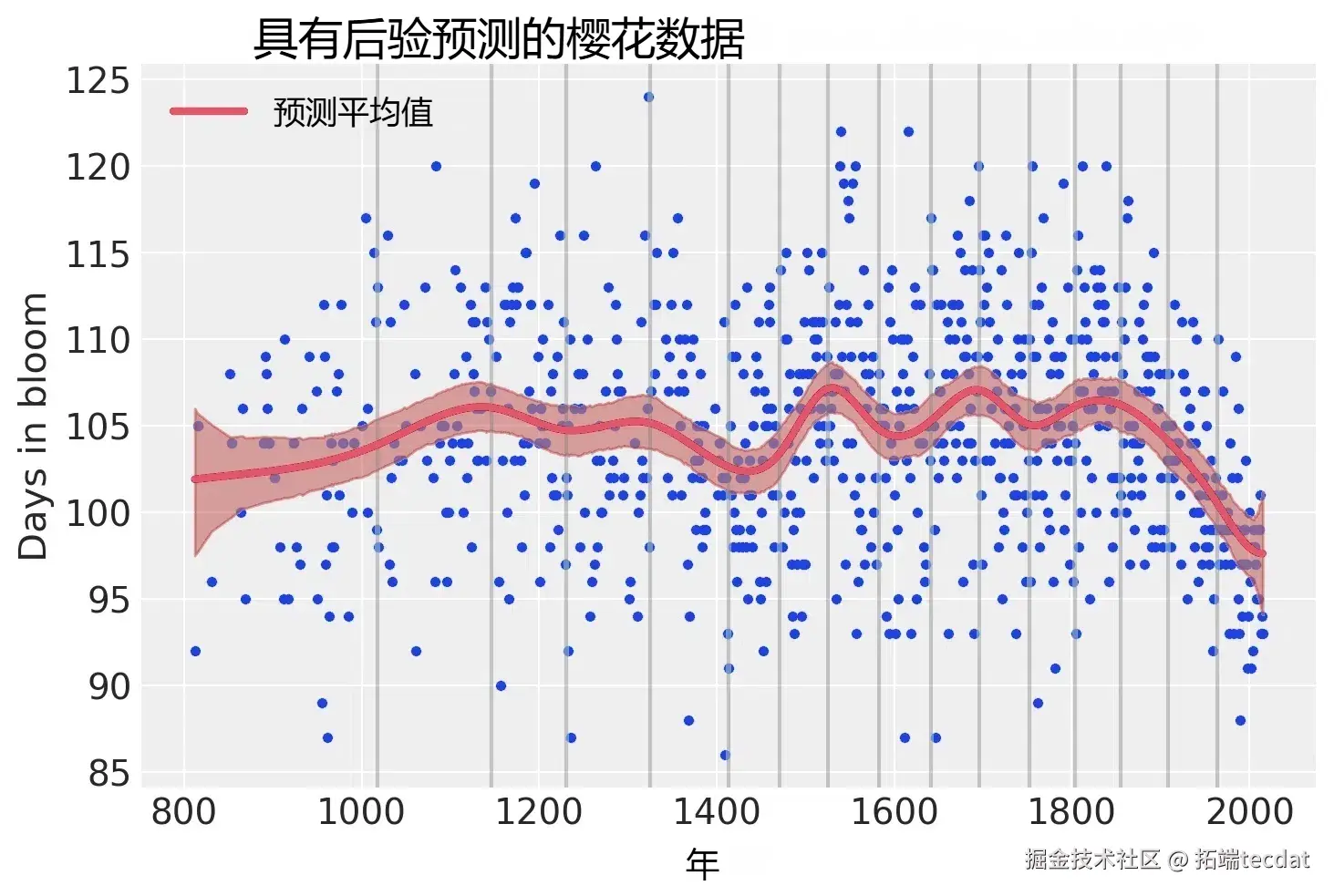
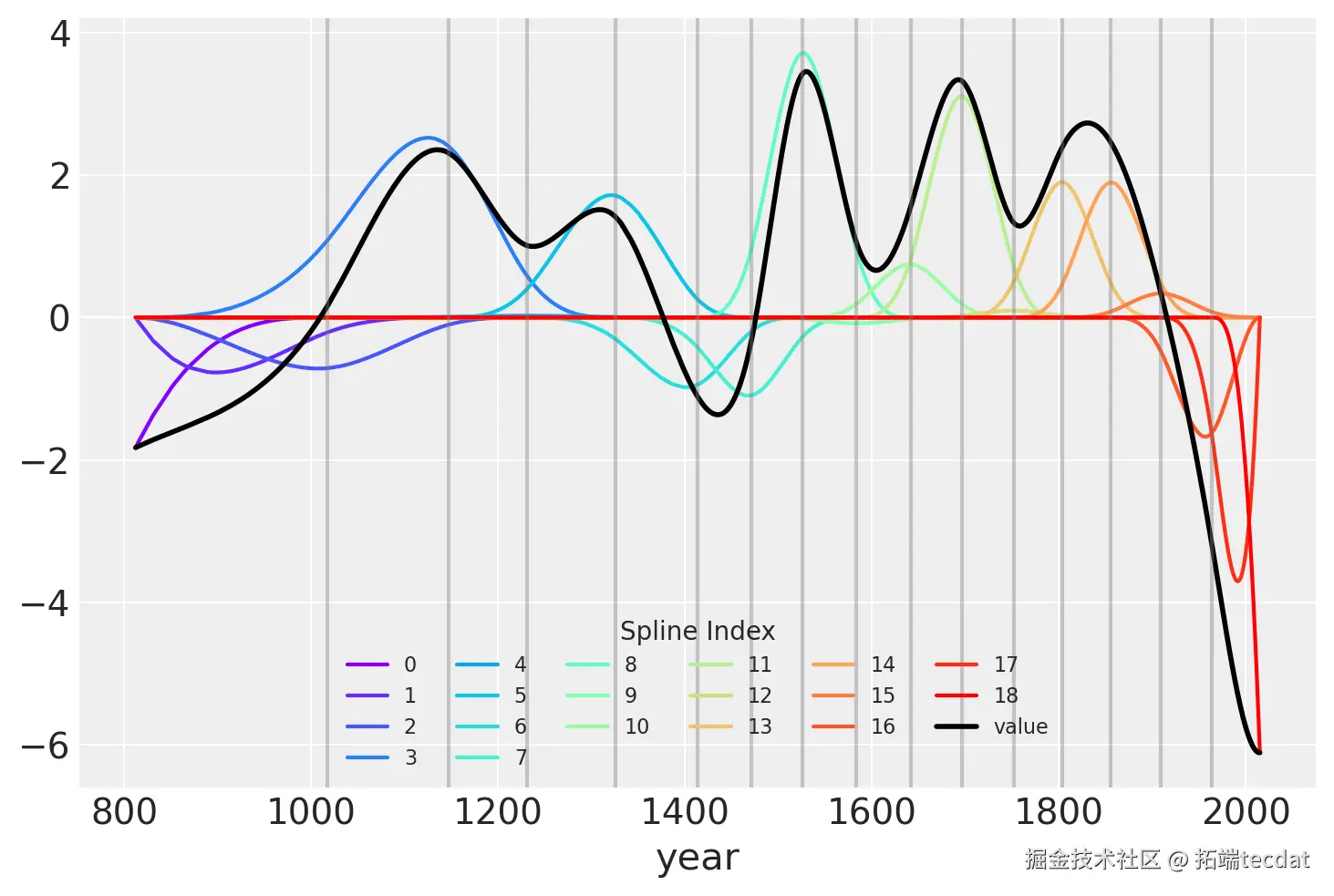
另一种可视化拟合样条值的方法是绘制它们与基矩阵的乘积。节点边界再次显示为垂直线，但现在样条基与w的值相乘（表示为彩虹色曲线）。B和w的点积——线性模型中的实际计算——以黑色显示。
pd.DataFrame(B * wp.T)
通过可视化模型预测结果，我们可以看到模型在原始数据上的拟合效果。
for knot in knot_list:
plt.gca().axvline(knot, color="grey", alpha=0.4)
\
新数据预测
- AI提示词：使用PyMC库重新定义模型，添加Data容器，将原始数据中的年份和开花天数作为Data变量，设置模型的坐标信息，构建样条基矩阵等
year_data = pm.Data("year", cherry_blossom_data.year)
w = pm.Normal("w", mu=0, sigma=3, dims="spline")
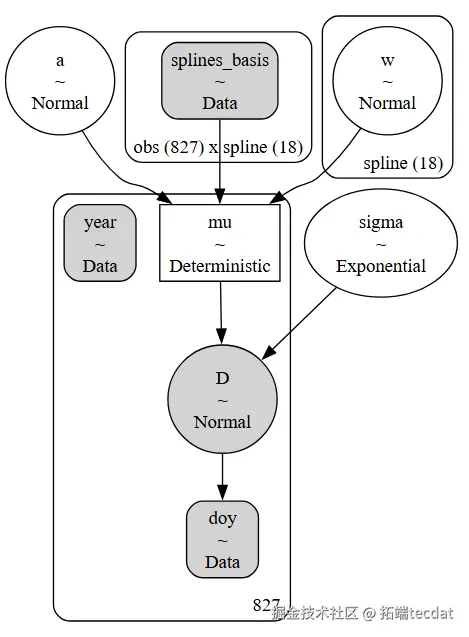
idata = pm.sample(
nuts_sampler="nutpie",
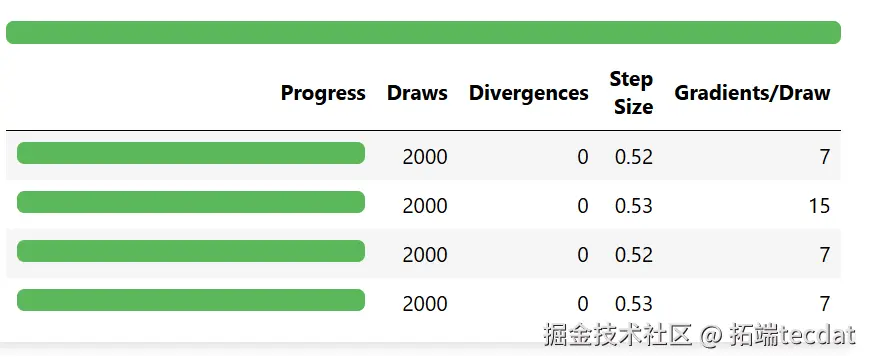
现在我们可以替换数据并使用新数据更新设计矩阵：
cherry_blossom_data.sample(50,
使用set_data更新模型中的数据：
new_data={
"year": year_data_new,
而剩下的就是从后验预测分布中进行抽样：
pm.sample_posterior_predictive(idata, var_names=["mu"])
绘制预测结果，以检查是否一切正常：
cherry_blossom_data.plot.scatter(
"year",
"doy",
\
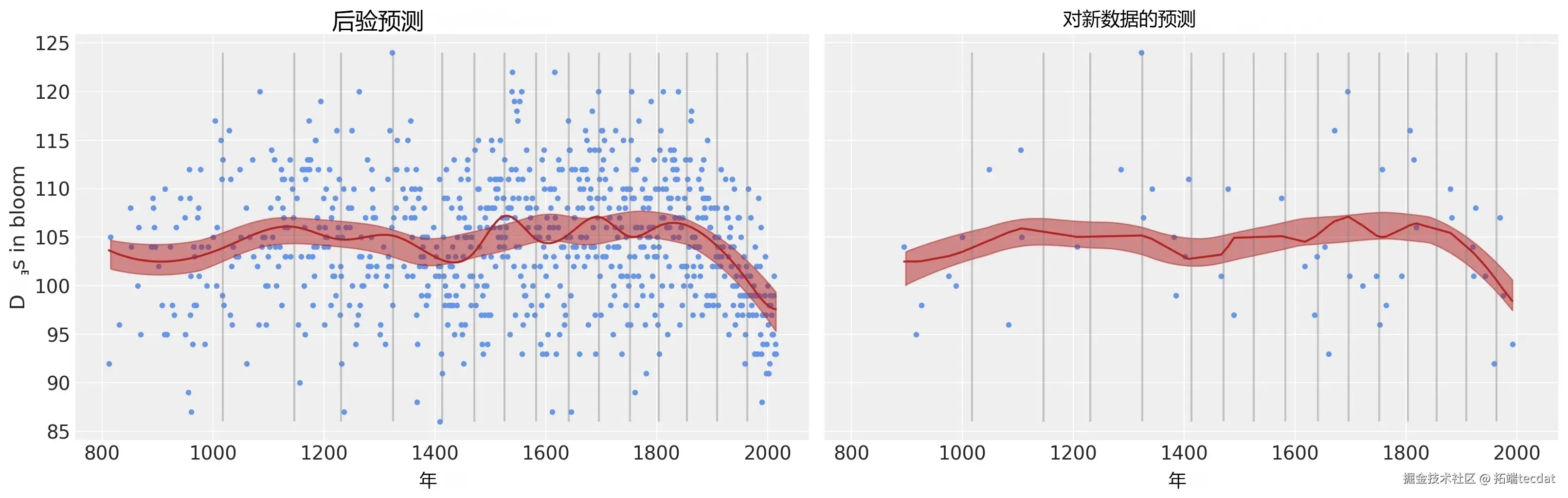
结论
通过本专题合集的研究，我们详细地展示了如何使用PyMC软件对樱花花期数据进行样条拟合分析。从数据的获取和处理，到模型的构建、拟合、分析以及新数据预测，每个环节都进行了深入的探讨。
在数据准备阶段，我们对原始的樱花花期数据进行了清洗，剔除了缺失值，为后续的分析奠定了基础。模型构建时，基于正态分布建立了合理的模型结构，引入了样条拟合的方法来捕捉数据中的非线性关系。通过精心设置模型参数的先验分布，使得模型更加合理可靠。
在模型拟合过程中，利用PyMC强大的抽样功能，获取了模型参数的后验分布。通过对后验分布的分析，我们发现模型参数的估计结果符合预期，并且模型的收敛性良好，链已经充分混合，这表明我们的模型能够较好地拟合数据。
在模型分析方面，通过对参数估计的详细解读，我们了解了每个参数在模型中的作用和影响。同时，通过绘制各种可视化图形，如迹图、森林图等，直观地展示了模型的性能和参数的分布情况。模型预测部分，我们不仅对原始数据进行了预测，还展示了如何使用模型对新数据进行预测，尽管样条拟合方法存在不能外推到原始数据范围之外的局限性，但在已知数据范围内，模型能够给出较为准确的预测结果。
本专题合集的研究成果对于理解和应用样条拟合方法具有重要的参考价值，希望能够为相关领域的研究和实践提供有益的指导，帮助数据科学领域的从业者和爱好者更好地应用数据分析方法解决实际问题，同时也为进一步探索和改进数据分析方法提供了思路。
Python贝叶斯分层模型专题|对环境健康、医学心梗患者、体育赛事数据空间异质性实证分析合集|附数据代码
专题|Python梯度提升实例合集：GBM、XGBoost、SMOTE重采样、贝叶斯、逻辑回归、随机森林分析信贷、破产数据
专题|Python贝叶斯金融数据应用实例合集：随机波动率SV模型、逻辑回归、参数更新、绩效比较BEST分析亚马逊股票、标准普尔500指数|附数据代码
R语言+AI提示词：贝叶斯广义线性混合效应模型GLMM生物学Meta分析
