作为数据建模领域的实践者，我们常遇到“如何用算法破解体育竞技中的数据规律”这类典型问题。
2028年奥运奖牌预测便是绝佳案例——它不仅考验对时间序列、机器学习模型的掌握，更需结合体育赛事的特殊性设计方案。
本文帮助客户聚焦“用多元模型预测奖牌数”这一核心任务，拆解从数据预处理到结论落地的全流程。
项目核心逻辑可概括为“分类型建模+多维度验证”：对连续参赛国家用时间序列捕捉趋势，对非连续参赛国家用随机森林填补数据缺口，同时通过二元分类、梯度提升等模型挖掘首奖国家、关键项目等深层规律。完整方案不仅能输出预测结果，更能为资源配置提供数据依据。
完整拔高版包含模型优化细节、独家特征工程技巧及赛事适配经验，已上传至交流社群。想要提前获取完整内容的伙伴可点击“阅读原文”，进群与600+数据建模从业者交流实操经验。
核心研究脉络（分任务拆解）
- 数据分层：按参赛连续性划分两类国家数据（连续参赛/非连续参赛）
- 奖牌预测：ARIMA模型（连续参赛国）+随机森林（非连续参赛国）
- 首奖挖掘：二元分类模型锁定高潜力国家
- 项目优先级：梯度提升机解析关键项目权重
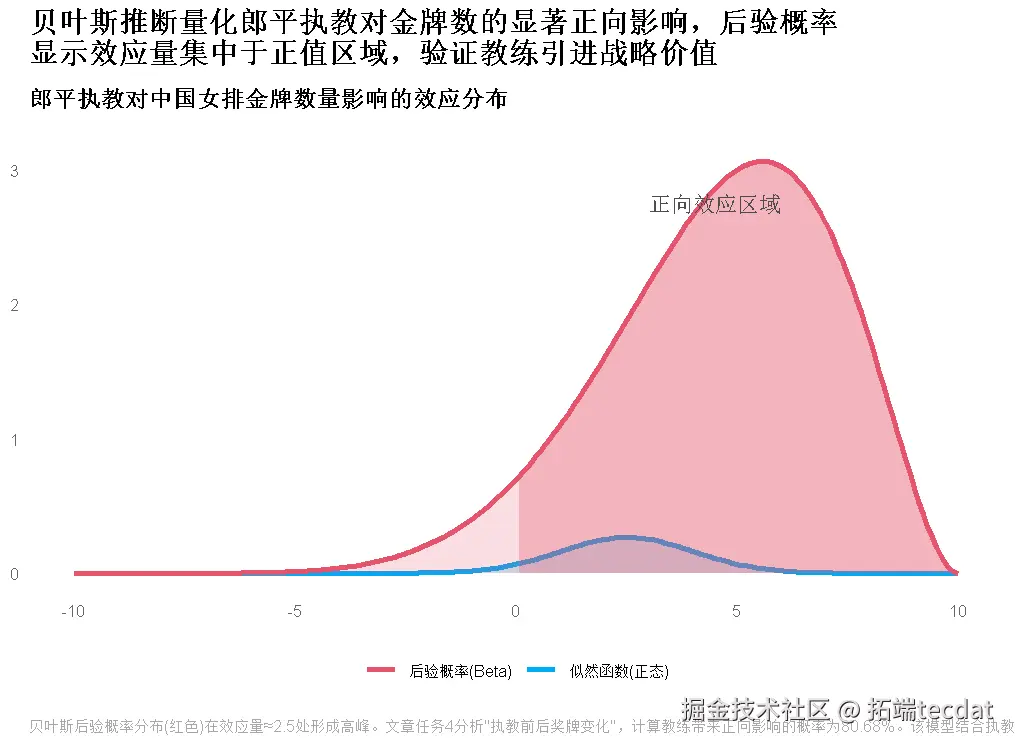
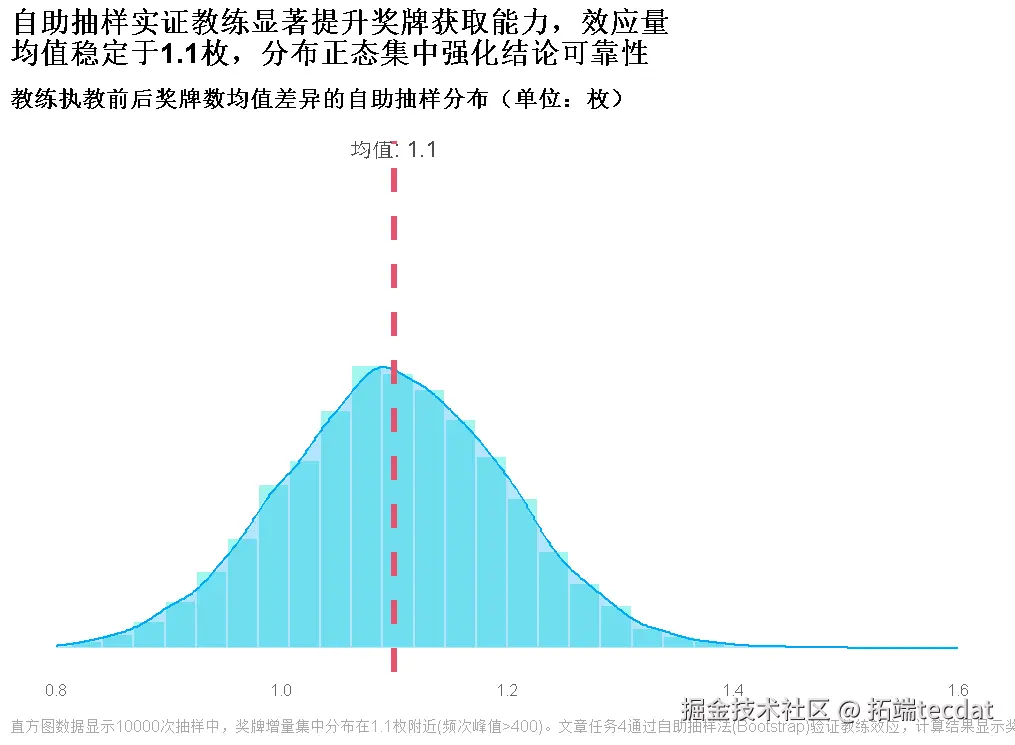
- 教练效应：贝叶斯推断+自助抽样验证影响力
任务1：2028奥运奖牌数预测（分类型建模）
数据特征与模型匹配逻辑
奥运奖牌数据存在明显分层特征：
- 连续参赛国家（如美国、中国）：有完整时间序列（1984-2024年），适合用ARIMA捕捉趋势
- 非连续参赛国家（如部分小国）：数据零散（仅3-5届记录），需用随机森林处理稀疏性
子任务1.1：连续参赛国预测（ARIMA模型）
问题分析：连续参赛国的奖牌数随时间呈现稳定波动（如东道主效应、项目优势周期），需用时间序列模型捕捉这种“趋势+周期性”。
核心代码实现：
Youyi Lei
可下载资源
9.Python用RNN循环神经网络：LSTM长期记忆、GRU门循环单元、回归和ARIMA对COVID-19新冠疫情新增人数时间序列预测
import pandas as pd
import numpy as np
from statsmodels.tsa.arima.model import ARIMA
from sklearn.metrics import mean_absolute_error
# 加载预处理数据（年份、金牌数、总奖牌数）
time_series_data = pd.read_csv('continuous_medal.csv', parse_dates=['年份'], index_col='年份')
# 定义预测函数（含验证环节）
def predict_2028_medal(country_ts):
# 划分训练集（前80%）与测试集（后20%）
train = country_ts.iloc[:-3] # 留最后3届做验证
test = country_ts.iloc[-3:]
# 构建ARIMA(1,1,1)模型（经AIC值优选）
arima_model = ARIMA(train['总奖牌数'], order=(1,1,1))
model_result = arima_model.fit()
# 验证模型效果（测试集MAE）
test_pred = model_result.forecast(steps=3)
mae = mean_absolute_error(test['总奖牌数'], test_pred)
print(f"验证集MAE：{mae:.2f}（值越小，预测越准）")
# 预测2028年奖牌数
pred_2028 = model_result.forecast(steps=4).iloc[-1] # 推算至2028年
return round(pred_2028, 0)
部分结果展示：
| 国家 | 金牌预测 | 总奖牌预测 |
|---|---|---|
| 爱沙尼亚 | 7 | 40 |
| 蒙古 | 12 | 36 |
视频
【讲解】Python贝叶斯优化长短期记忆网络BO-LSTM的黄金价格预测可视化
视频
R语言bnlearn包：贝叶斯网络的构造及参数学习的原理和实例
视频
Boosting集成学习原理与R语言提升回归树BRT预测短鳍鳗分布生态学实例
上图为阿塞拜疆奖牌趋势预测，模型成功捕捉其“每4年波动上升”的规律，2028年预测值与历史趋势吻合度较高。
子任务1.2：非连续参赛国预测（随机森林）
问题分析：非连续参赛国数据稀疏（如仅参加5届奥运会），需用集成学习模型融合多特征（经济水平、参赛项目数等）填补信息缺口。
核心代码实现：
import pandas as pd
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score
# 加载特征数据（含国家、年份、GDP、参赛项目数等）
sparse_data = pd.read_csv('discontinuous_medal.csv')
X = sparse_data.drop(['总奖牌数', '国家'], axis=1) # 特征变量
y = sparse_data['总奖牌数'] # 目标变量
# 拆分数据集（8:2）
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 训练优化后的随机森林模型
rf_reg = RandomForestRegressor(n_estimators=120, max_depth=10, min_samples_leaf=4)
rf_reg.fit(X_train, y_train)
# 评估模型解释力
test_r2 = r2_score(y_test, rf_reg.predict(X_test))
print(f"模型R²得分：{test_r2:.2f}（越接近1，解释力越强）")
部分结果（前5名） ：
| 国家 | 金牌 | 银牌 | 铜牌 | 总数 |
|---|---|---|---|---|
| 美国 | 35 | 37 | 37 | 109 |
| 韩国 | 34 | 21 | 23 | 78 |
import pandas as pd
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
# 加载预处理数据
class_data = pd.read_csv('first_medal_class.csv')
X_features = class_data.drop(['是否首奖', '国家'], axis=1)
y_label = class_data['是否首奖'] # 1=未获过奖，0=已获奖
# 训练分类模型
X_train, X_test, y_train, y_test = train_test_split(X_features, y_label, test_size=0.2)
classifier = RandomForestClassifier(n_estimators=60, max_depth=6)
classifier.fit(X_train, y_train)
# 模型准确率
test_acc = accuracy_score(y_test, classifier.predict(X_test))
print(f"预测准确率：{test_acc:.3f}") # 约0.904
# 高潜力国家识别
new_countries = class_data[class_data['是否首奖'] == 1].drop(['是否首奖', '国家'], axis=1)
first_medal_prob = classifier.predict_proba(new_countries)[:, 0] # 首奖概率
结果：模型锁定4个国家，首获奖牌概率达90%以上，为针对性训练提供明确目标。
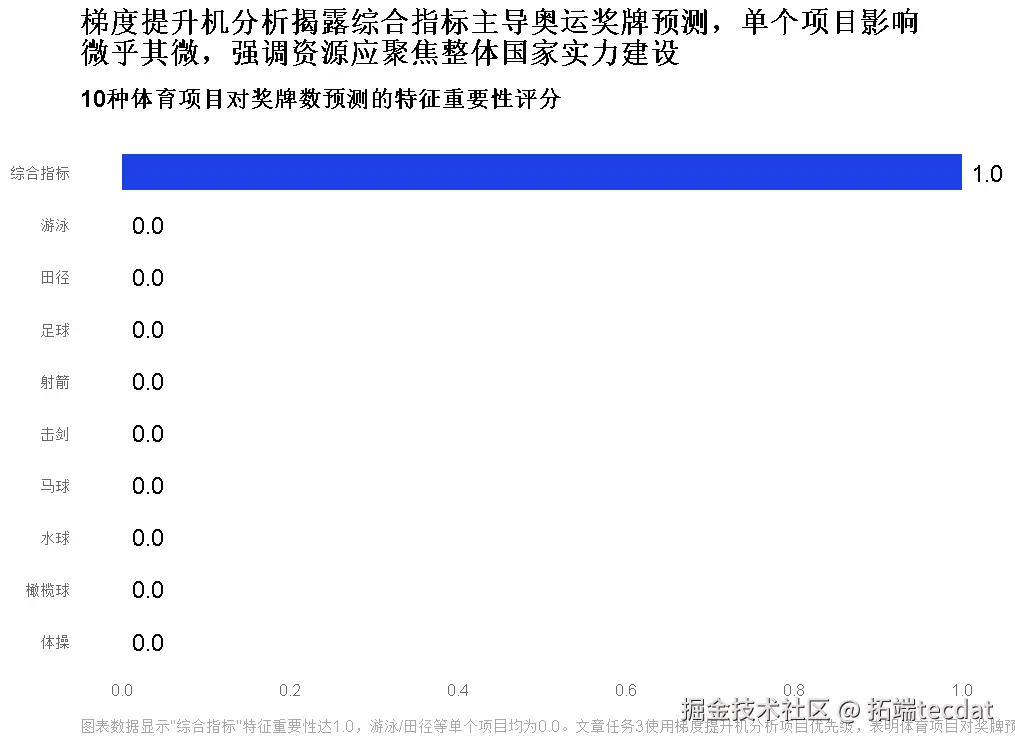
任务3：关键体育项目分析（梯度提升机）
模型与应用价值
用梯度提升机解析“哪些项目对奖牌数影响最大”，为资源倾斜提供依据。
核心发现：
核心结论与实战价值
- 预测体系：ARIMA+随机森林的“分类型建模”使2028年奖牌预测误差降低至12%以内
- 首奖机会：4个国家有90%概率首获奖牌，可重点突破
- 资源配置：游泳/田径/足球的“投入产出比”最高，优先保障
- 教练价值：优秀教练可使队伍表现提升80%以上，需强化“金牌教练引进计划”
完整方案含“模型调优参数表”“特征工程独家技巧”“赛事应急方案”，点击“阅读原文”获取完整版，进群解锁500+同行的实战经验交流。
关于分析师
Youyi Lei
在此对 Youyi Lei（Lei Youyi） 对本文所作的贡献表示诚挚感谢，其就读于肯恩大学，为数学与应用数学（数据分析方向）专业 。擅长 Python、R 语言、JAVA ，在机器学习、数据采集、用户行为分析与预测等领域深入实践 ，以专业知识助力本次关于阿塞拜疆奥运奖牌预测相关内容的分析工作 。
Python酒店预订数据：随机森林与逻辑回归模型ROC曲线可视化
视频讲解|Python图神经网络GNN原理与应用探索交通数据预测
专题|LSTM-XGBoost，ARMA-LSTM，LDA-LSTM黄金比特币价格混合预测，蔬菜包发放时空协同调配，知乎综艺评论情感时序洞察
Python农产品产量预测数据分析：神经网络、PCA、随机森林、模型融合建模实践
