最近我们被客户要求撰写关于检测异常值的研究报告，包括一些图形和统计输出。
此示例显示了Hampel用于检测和删除异常值的过程的实现。产生一个包含24个样本的随机信号x。 重置随机数生成器以获得可重复的结果。
可下载资源
rng default
lx = 24;
x = randn(1,lx);通常我们会使用程序判断滤波的方式来过滤异常数据，比如说先对一个序列求平均值，方差等等，然后对每个数据和平均值或方差的偏差，设置一个阈值，差超过这个阈值就认为是异常数据，然后过滤。当然这个阈值只能是经验值，有时候不一定准确，或当异常数据变成常态的时候，异常数据就不再是异常数据，这时候如果还是使用阈值过滤就会有一些问题。当然程序判断滤波的方式还是适用于一些场景，并且实现比较方便。
在做数据统计，分析以及图像处理中，为了防止噪声对数据结果的影响，除了采用更加科学的采样技术外，我们还要采用一些必要的技术手段对原始数据进行整理、统计。数字滤波技术是最基本的处理方法，它可以剔除数据中的噪声，提高数据的代表性。常用的滤波技术有：程序判断滤波，均值滤波，中值滤波，加权平均，滤波，众数滤波，一阶滞后滤波，移动滤波，复合滤波等。
围绕x的每个元素生成观察窗口。 在样本的任一边取k = 2个邻居。 产生的移动窗口的长度为2×2 + 1 = 5个样本。
k = 2;
iLo = (1:lx)-k;
iHi = (1:lx)+k;截断窗口，以便函数在到达信号边缘时计算较小段的中值。
iLo(iLo<1) = 1;
iHi(iHi>lx) = lx;记录每个周围窗口的中位数。 找到每个元素相对于窗口中位数的绝对偏差的中位数。
for j = 1:lx
w = x(iLo(j):iHi(j));
medj = median(w);
mmed(j) = medj;
mmad(j) = median(abs(w-medj));
end缩放中位数绝对偏差
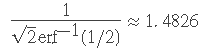
以获得正态分布标准偏差的估计值。
sd = mmad/(erfinv(1/2)*sqrt(2));
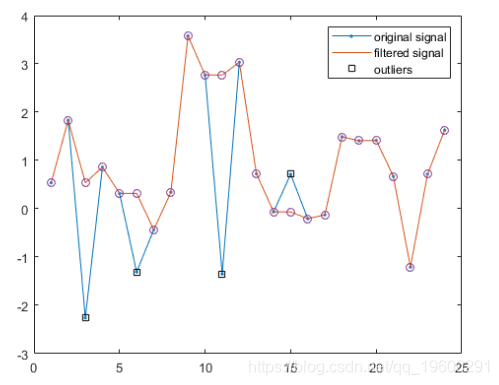
查找与中位数相差超过nd = 2个标准偏差的样本。 将这些离群值替换为其周围窗口的中间值。 这是Hampel算法的本质。
yu = x;
yu(ki) = mmed(ki);使用hampel 计算滤波后的信号并注释异常值。 覆盖在此示例中计算的过滤值。
plot(yu,'o','HandleVisibility','off')
MATLAB用CNN-LSTM神经网络的语音情感分类深度学习研究
Python用KNN（K-近邻）回归、分类、异常值检测预测房价、最优K值选取、误差评估可视化
MATLAB模糊C均值聚类FCM改进的推荐系统协同过滤算法分析MovieLens电影数据集
Python、MATLAB股票投资：ARIMA模型最优的选股方案和投资组合方案与预测
