在本文中我们用R语言模拟混合制排队随机服务排队系统。
M / M / 1系统
该系统的基本参数::
可下载资源
使用M / M / 1系统进行仿真非常简单 。
排队论 (queuing theory)，或称随机服务系统理论， 是通过对服务对象到来及服务时间的统计研究，得出这些数量指标（等待时间、排队长度、忙期长短等）的统计规律，然后根据这些规律来改进服务系统的结构或重新组织被服务对象，使得服务系统既能满足服务对象的需要，又能使机构的费用最经济或某些指标最优。它是数学运筹学的分支学科，也是研究服务系统中排队现象随机规律的学科。广泛应用于计算机网络、生产、运输、库存等各项资源共享的随机服务系统。 排队论研究的内容有 3 个方面：统计推断，根据资料建立模型；系统的性态，即和排队有关的数量指标的概率规律性；系统的优化问题。其目的是正确设计和有效运行各个服务系统，使之发挥最佳效益。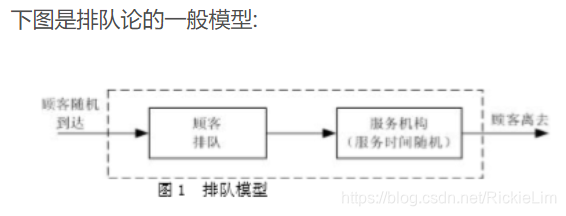
图中虚线所包含的部分为排队系统。各个顾客从顾客源出发，随机地来到服务机构，按一定的排队规则等待服务，直到按一定的服务规则接受完服务后离开排队系统。
凡要求服务的对象统称为顾客，为顾客服务的人或物称为服务员，由顾客和服务员组成服务系统。对于一个服务系统来说，如果服务机构过小，以致不能满足要求服务的 众多顾客的需要，那么就会产生拥挤现象而使服务质量降低。 因此，顾客总希望服务机构越大越好，但是，如果服务机构过大，人力和物力方面的开支也就相应增加，从而 会造成浪费，因此研究排队模型的目的就是要在顾客需要和服务机构的规模之间进行权衡决策，使其达到合理的平衡。
lambda <- 2
mu <- 4
rho <- lambda/mu # = 2/4
..
例如， 可以快速可视化随时间变化的资源使用情况。在下面，我们可以看到仿真如何收敛到系统中理论上的平均客户数。
# 理论值
mm1.N <- rho/(1-rho)
graph + geom_hline(yintercept=mm1.N)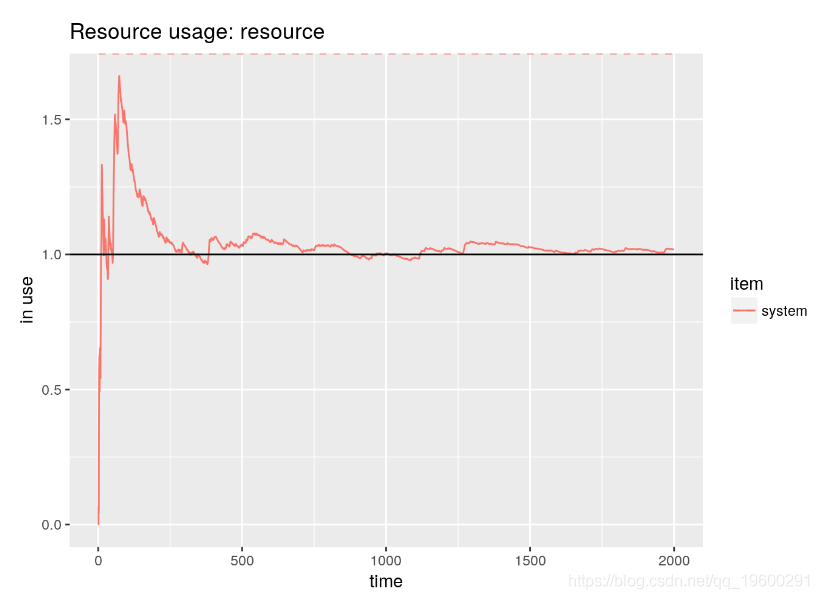
例如，还可以通过使用参数items和来可视化各个元素的瞬时steps。
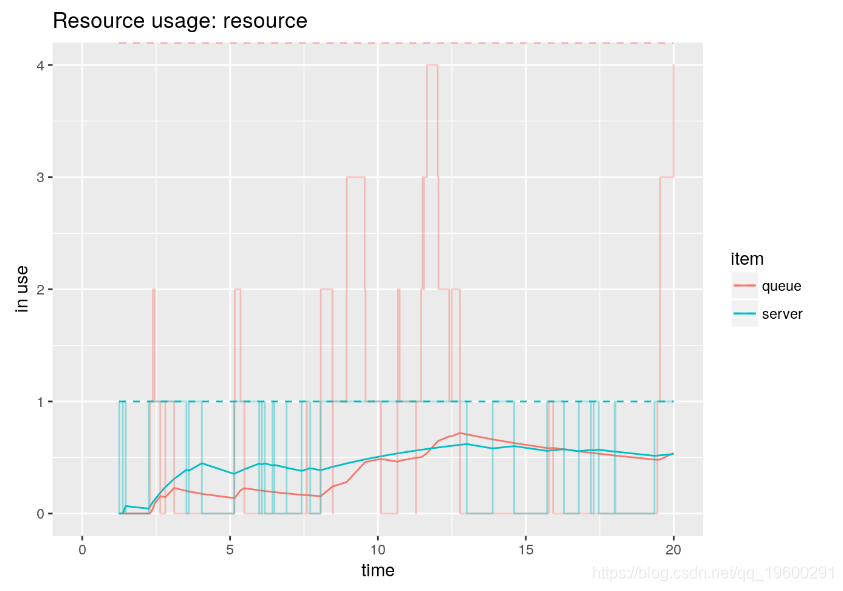
我们可以获取系统中每个客户花费的时间，并将平均值与理论表达式进行比较。
## [1] 0.5## [1] 0.5012594看来它与理论值非常吻合。
并行化的缺点是，当每个线程完成时，我们会丢失基础的C ++对象 。让我们执行一个简单的测试：
library(dplyr)
t_system <- get_mon_arrivals(envs) %>%
mutate(t_system = end_time - start_time) %>%
group_by(replication) %>%
summarise(mean = mean(t_system))
t.test(t_system$mean)##
## One Sample t-test
##
## data: t_system$mean
## t = 348.23, df = 999, p-value < 2.2e-16
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
## 0.4957328 0.5013516
## sample estimates:
## mean of x
## 0.4985422最后，M / M / 1满足了系统中所用时间的分布，而该分布又是具有平均值的指数随机变量。
qqplot(mm1.t_system, rexp(length(mm1.t_system), 1/mm1.T))
abline(0, 1, lty=2, col="red")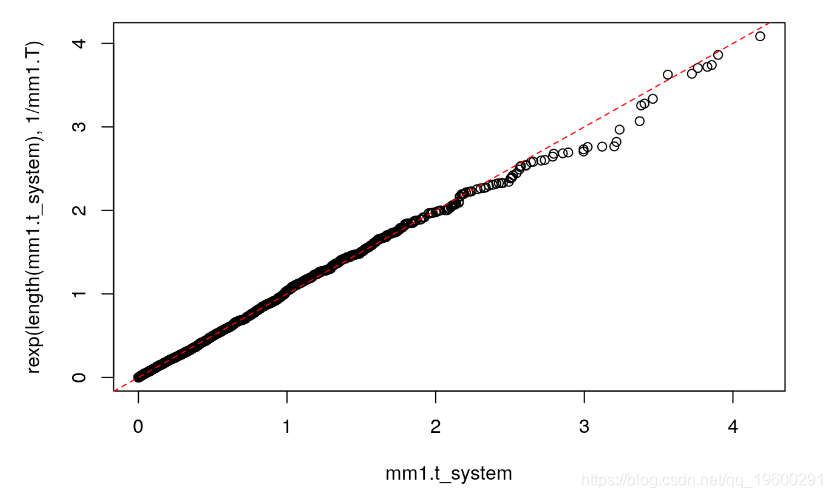
M / M / c / k系统
M / M / c / k系统保持指数到达和服务时间，但通常具有不止一台服务器和有限的队列，这通常更现实。例如，路由器可能有多个处理器来处理数据包，而输入/输出队列必定是有限的。
这是M / M / 2/3系统（2个服务器，队列中1个位置）的模拟。
lambda <- 2
mu <- 4
mm23.trajectory <- create_trajectory() %>%
...
在这种情况下，队列已满时会有拒绝。
## rejection_rate
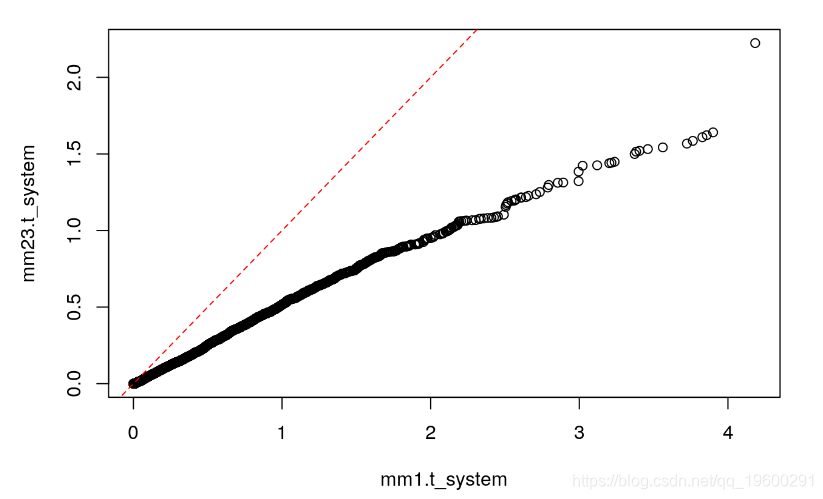
## 1 0.02009804尽管如此，与M / M / 1情况一样，系统中花费的时间仍遵循指数随机变量，但平均值有所下降。
# Comparison with M/M/1 times
qqplot(mm1.t_system, mm23.t_system)
abline(0, 1, lty=2, col="red")
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
R语言蒙特卡罗Monte Carlo方法进行数值积分和模拟可视化
R语言非线性动态回归模型ARIMAX、随机、确定性趋势时间序列预测个人消费和收入、用电量、国际游客数量
【视频】因子分析简介及R语言应用实例：对地区经济研究分析重庆市经济指标
R语言布朗运动模拟股市、物种进化树状图、二项分布可视化
