python算法对音频信号处理Sonification ：Gauss-Seidel迭代算法

可以将44.1kHz单通道.wav文件中的一秒读取到长度为44100的数组（称为b）中。给定矩阵A，我们寻求系统Ax = b的解。通过Gauss-Seidel的迭代，向量Ax将接近b，而Ax的高频部分首先接近b。如果我们将b用作歌曲录音，则将一些白噪声作为我们的初始猜测，并在每次迭代中写出Ax，我们会观察到b中高音调的音符首先变得可听，而同时白噪声的音调减小。

最初的12秒.wav文件的音频（白噪声）initialAx.wav

初始Ax，残差和残差FFT的图：

  ​

​

​

---

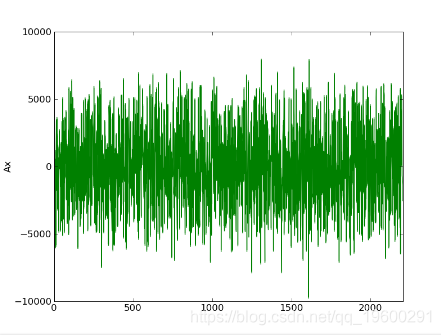
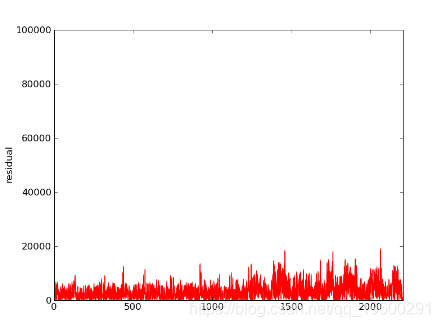
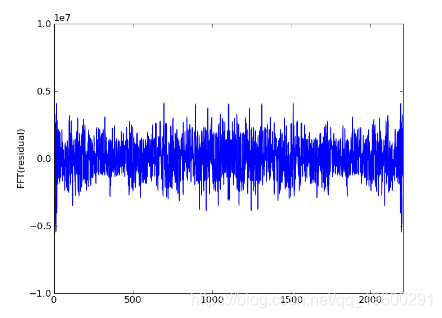
经过一轮迭代，高音变为gauss_seidel_out000000.wav

在光谱中可以看到一些结构：

  ​​​

---

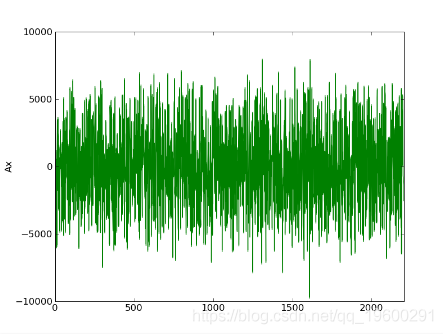
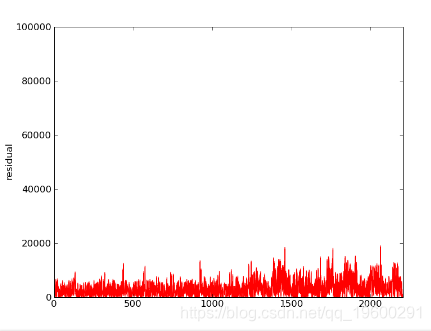
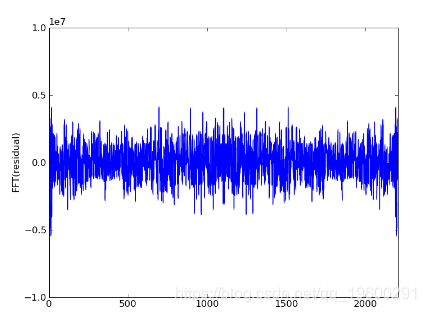
第二次迭代：gauss_seidel_out000001.wav

  ​​​

---

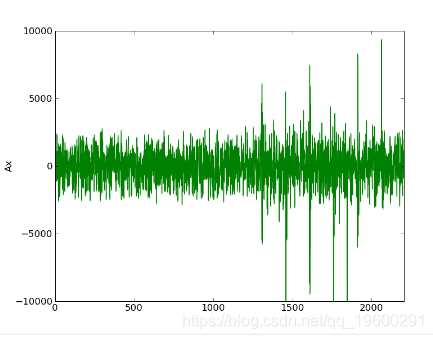
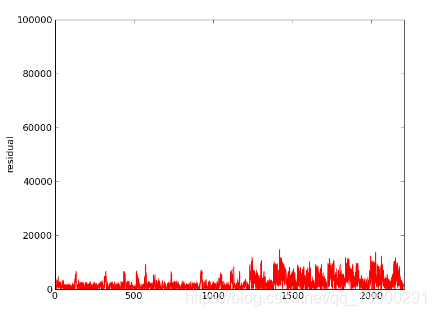
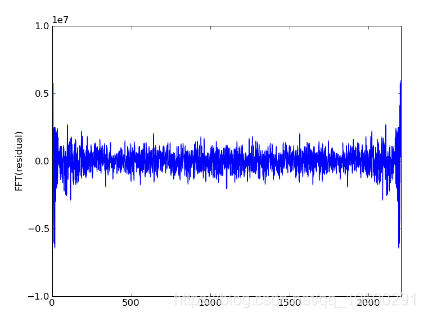
第三次迭代：gauss_seidel_out000002.wav

  ​​​

---

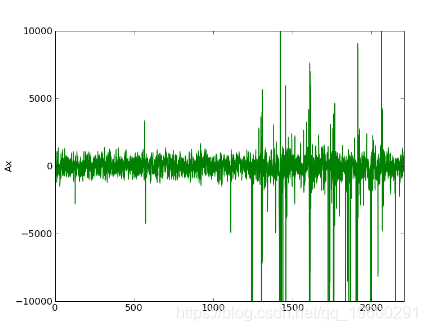
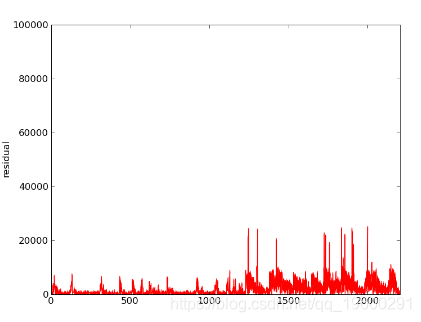
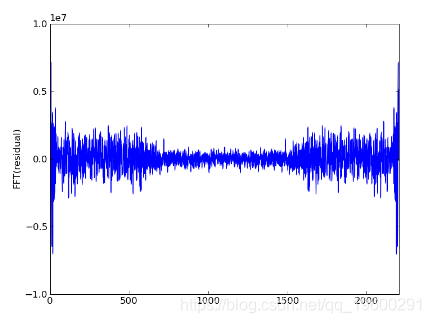
第四次迭代：gauss_seidel_out000003.wav

  ​​​

---

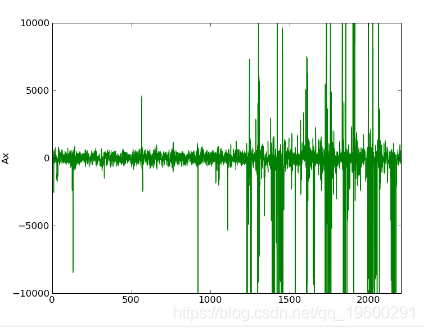
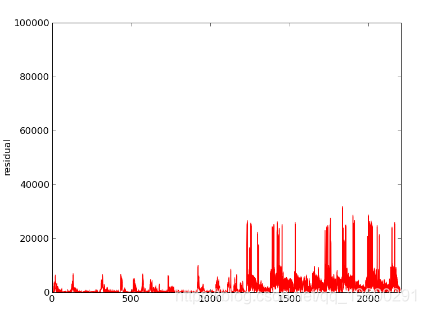
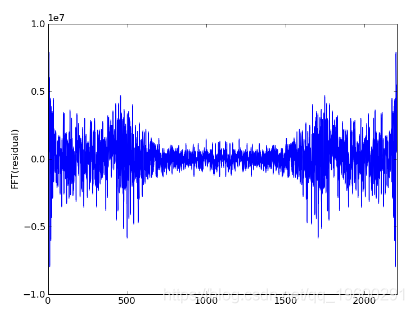
这一切都在python中完成。将.wav文件加载到数组中，在scipy中还不错。为了避免内存问题，必须使用稀疏矩阵类，因为12秒的.wav文件需要一个大小为12 * 44100的数组。这是我使用的TridiagonalMatrix类代码片段：

from numpy import *

#a tridiagonal matrix class
class TridiagonalMatrix:
    #initialize with 3 numpy arrays
    def __init__(self, upper_in, diag_in, lower_in):
        self.upper  = upper_in
        self.diag   = diag_in
        self.lower  = lower_in
        self.dim    = diag_in.shape[0]
    #matrix mulitplication
    def apply(self, v):
        out = ndarray(self.dim)
        try:
            out[0] = self.diag[0]*v[0] + self.upper[0]*v[1]
            out[self.dim-1] = self.lower[self.dim-2]*v[self.dim-2] + self.diag[self.dim-1]*v[self.dim-1]
            for i in range(1, self.dim-1):
                out[i] = self.lower[i-1]*v[i-1] + self.diag[i]*v[i] + self.upper[i]*v[i+1]
        except(IndexError):
            print "Wrong sizes"

        return out

    

这是处理读取/写入.wav文件然后使用Gauss-Seidel迭代求解线性系统的代码片段。

from TridiagonalMatrix import *
from numpy import *
from scipy.io import wavfile
import scipy.fftpack
import pylab
import sys
import os

def musical_gauss_seidel(A, b, x0, tol):
"""
do the gauss seidel iteration
but output some sound every now and then..
A is some matrix that lets gauss seidel work
b is a vector that represents a .wav file of a pretty song
x0 is our initial guess for the gauss seidel method (probably random static)
we are going to output the .wav data corresponding to Ax
as Ax gets closer to b (ie the residual gets smaller)
we should hear the song emerge from the initial guess
"""
    #make noise of the initial approximation to b
    wavfile.write("gauss_seidel_out000000.wav", 44100, (A.apply(x0)).astype(int16))

    residual  = A.apply(x0) - b