但量表数据的多样性、量化指标的差异性的问题，导致传统评价方法易出现主观性强、分类模糊的痛点。作为数据分析师，我们在过往客户咨询项目中发现，单一方法难以兼顾分类准确性与评价客观性，因此探索出多算法融合的解决方案——通过聚类、降维、统计检验与客观赋权方法结合，构建适配多心理量表的数据处理体系。 本文围绕SL-90症状自评量表、职业成熟度量表、大五人格量表三类数据，搭建从数据预处理到评价验证的全流程模型，依次实现量表分类、综合聚类、分组差异研判与评价方法校验。模型核心创新在于将熵权TOPSIS法与K-means聚类结合，通过客观赋权规避人为权重偏差，同时用K折交叉验证保障结果可靠性。 本文内容改编自过往客户咨询项目的技术沉淀并且已通过实际业务校验，该项目完整代码与数据已分享至交流社群。阅读原文进群，可与800+行业人士交流成长；还提供人工答疑，拆解核心原理、代码逻辑与业务适配思路，帮大家既懂 怎么做，也懂 为什么这么做；遇代码运行问题，更能享24小时调试支持。

项目文件目录

数据预处理与核心方法概述

数据基础

本次采用三类核心心理量表数据，分别从心理症状（SL-90症状自评量表）、职业适配度（职业成熟度量表）、人格特质（大五人格量表）三个维度采集信息，覆盖168名评估对象，为后续分析提供全面数据支撑。

预处理流程

首先对原始数据进行清洗：剔除极端异常值，针对空白值采用众数填补法补全，确保数据完整性。此步骤可规避残缺数据对后续模型的干扰，为分析结果可靠性奠定基础。

核心方法简化说明

1. 频数分析：将各量表得分划分为四类区间，通过区间分布实现评估对象分类，结合分布特征验证分类科学性。
2. Kendall’s W检验：检验多量表分类结果的一致性，W值越接近1，表明分类结果关联性越强。
3. PCA主成分分析：将三维量表数据降维至二维，在保留86%以上信息的前提下简化计算，提升后续聚类效率。
4. K-means聚类：基于降维后的数据划分聚类簇，通过距离平方和确定最优簇数，实现评估对象的综合分类。
5. T检验：对比两组评估对象的量表数据，通过均值、标准差等指标研判组间差异显著性。
6. 熵权TOPSIS法：通过信息熵计算各量表权重，结合TOPSIS法得出评估对象综合得分，实现客观评价。
7. K折交叉验证：将数据按9:1划分为训练集与验证集，通过准确率、召回率验证模型可靠性。

量表分类与关联性分析

分类实现

采用频数分析对三类量表分别完成分类，计算各得分区间的频数及占比，形成分类标准：评估对象得分落入对应区间，即可判定其所属类别。

分类结果验证

对三类量表的频数分布进行可视化分析，结果如下：



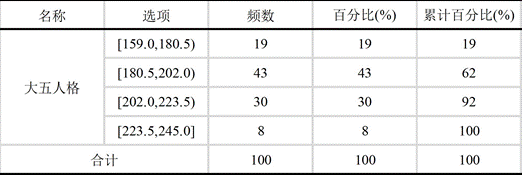
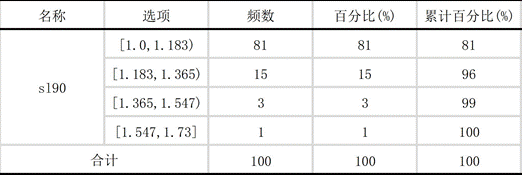
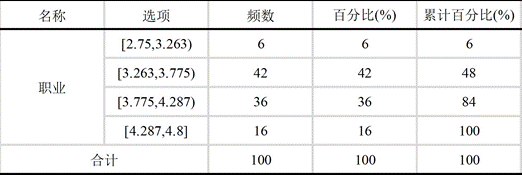
图1 三类量表频数统计图


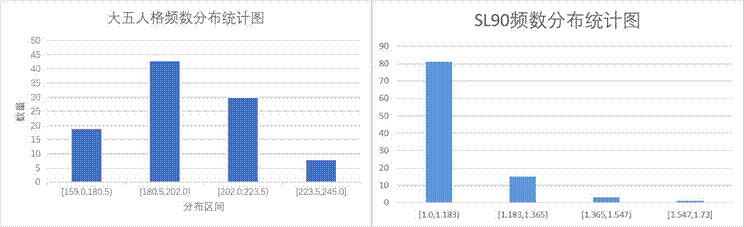
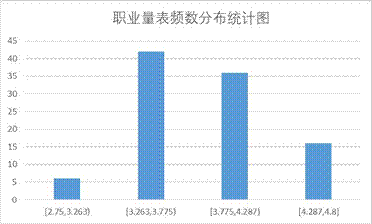
图2 频数分布条形统计图
从分布特征来看，职业成熟度量表与大五人格量表的频数分布接近正态分布，符合心理评估数据的普遍规律，证明分类标准具有科学性；SL-90量表某一区间占比达90%，因该量表用于心理健康筛查，健康人群占比偏高的结果贴合实际应用场景。

分类结果关联性检验

采用Kendall’s W检验验证三类量表分类结果的一致性，检验结果如下表所示：

名称	秩平均值	中位数	Kendall’s W系数	X²	P
SL-90	1	1.07	1	200	0.000***
大五人格	3	194.5	–	–	–
职业成熟度	2	3.78	–	–	–

注：***代表1%的显著性水平
检验结果显示Kendall’s W系数为1，表明三类量表的分类结果几乎完全相关，说明不同维度的心理评估具有一致性，为后续综合分析提供了合理性支撑。

综合评价体系构建与聚类分析

降维处理

先通过KMO检验与Bartlett检验验证数据适配性，检验结果显示KMO值为0.525，Bartlett球形度检验P值小于0.001，表明数据适合进行主成分分析。
采用PCA主成分分析对三类量表数据降维，提取特征根大于1的主成分，结果显示前两个主成分的累积方差解释率达86.917%，可充分保留原始信息。降维后各量表在主成分上的载荷系数如下：

量表	主成分1	主成分2	共同度
SL-90	-0.591	0.785	0.966
大五人格	0.784	0.49	0.855
职业成熟度	0.882	0.091	0.787

聚类实现

基于降维后的数据进行K-means聚类，通过对比不同簇数的距离平方和确定最优簇数为5，此时距离平方和降至2158.375，聚类效果较优。

聚类核心代码（MATLAB改写）

% 心理量表数据聚类分析（K-means算法）
psych_data = []; % 省略：导入降维后的主成分数据
cluster_num = 5; % 最优聚类簇数
[cluster_idx, centroids] = kmeans(psych_data, cluster_num); % 执行聚类
% 聚类结果可视化
color = {'r','g','b','c','m'};
figure
for i = 1:cluster_num
 cluster_data = psych_data(cluster_idx == i, :);
 scatter3(cluster_data(:, 1), cluster_data(:, 2), zeros(size(cluster_data,1),1), color{i},'o');
 hold on;
 scatter3(centroids(i, 1), centroids(i, 2), 0,'k','x');
end
hold off;
xlabel('主成分1');
ylabel('主成分2');
title('5簇K-means聚类分析');
legend({'簇1','簇2','簇3','簇4','簇5','簇中心'});
grid on;

代码功能：导入降维数据后，以5为簇数执行K-means聚类，通过散点图可视化聚类结果，标注各簇中心位置，直观呈现分类效果。

聚类结果分析

聚类结果如下表所示，5个簇的占比分别为34%、27%、16%、8%、15%，分布相对合理。

聚类类别	频数	百分比%
1	34	34
2	27	27
3	16	16
4	8	8
5	15	15
合计	100	100

各聚类中心对应的原始量表得分如下：

聚类种类	SL-90	大五人格	职业成熟度量表
1	1.115	187.559	3.553
2	1.132	201.481	3.865
3	1.103	168.625	3.708
4	1.030	231.125	4.325
5	1.062	216.533	4.252

可视化结果显示，各簇整体区分度良好，但簇1与簇2、簇2与簇5存在少量重叠，后续可通过算法优化提升分离度。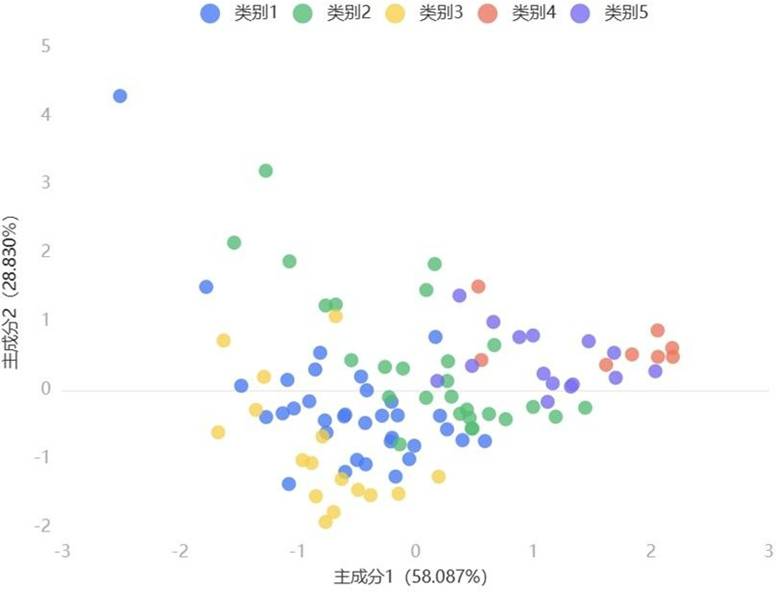

分组差异研判与评价方法验证

分组差异分析

采用T检验对比两组评估对象的量表数据，研判组间差异：SL-90量表两组数据的P值小于0.001，Cohen’s d为1.309，表明组间差异显著；大五人格量表P值为0.918，职业成熟度量表P值为0.001但Cohen’s d仅0.355，两组量表的组间差异不明显。
结果提示，两组评估对象的心理症状表现差异较大，而人格特质与职业适配度的差异较小，可为针对性心理服务提供方向。

评价方法准确性验证

采用熵权TOPSIS法构建综合评价模型，客观计算各量表权重，再通过K折交叉验证检验模型可靠性。

熵权计算结果

量表	信息熵值e	信息效用值d	权重(%)
大五人格	0.97	0.03	55.374
职业成熟度	0.981	0.019	34.307
SL-90	0.994	0.006	10.319

结果显示，大五人格量表权重最高，对综合评价的影响最大，符合人格特质在心理评估中的核心地位。

K折交叉验证核心代码（MATLAB改写）

% 心理评价模型K折交叉验证（验证准确率、召回率、精确度）
X = []; % 省略：导入量表特征数据
y = []; % 省略：导入分类标签数据
% 划分训练集与验证集（9:1比例）
cvp = cvpartition(size(X,1),'HoldOut',0.1);
X_train = X(cvp.training,:);
y_train = y(cvp.training,:);
X_val = X(cvp.test,:);
y_val = y(cvp.test,:);
% 训练模型并预测
model = fitcsvm(X_train, y_train); % 支持向量机模型训练
y_pred = predict(model, X_val); % 验证集预测
% 计算评价指标
confusionMatrix = confusionmat(y_val, y_pred);
accuracy = sum(diag(confusionMatrix)) / sum(sum(confusionMatrix));
recall = diag(confusionMatrix) / sum(confusionMatrix, 1);
precision = diag(confusionMatrix) / sum(confusionMatrix, 2);
% 输出结果
fprintf('准确率: %.4f\n', accuracy);
fprintf('召回率: %.4f\n', mean(recall));
fprintf('精确度: %.4f\n', mean(precision));

代码功能：按9:1比例划分数据，通过支持向量机训练模型，计算准确率、召回率、精确度三个指标，验证评价模型可靠性，最终结果显示准确率0.9492、召回率0.9128、精确度0.9389，模型表现优异。

聚类优化结果

基于熵权TOPSIS法的综合得分再次进行聚类，仍划分为5个簇，聚类结果的F值为556.892，P值小于0.001，表明各簇间差异显著。

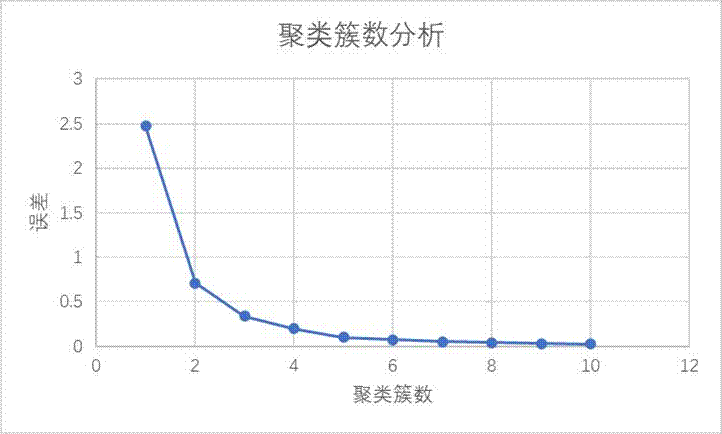
图3 熵权法评价聚类分析图

模型评价、优化与工具适配说明

模型优势与应用价值

优势在于多算法融合，通过客观赋权与交叉验证规避主观性，结果可靠性高；覆盖分类、聚类、差异分析、评价验证全流程，适配心理评估实际需求。可广泛应用于心理服务机构的评估筛查、人才选拔的心理适配度研判等场景。

优化方向

1. 数据层面：扩充评估对象样本量，纳入不同年龄段、职业背景的数据，提升模型泛化能力。
2. 算法层面：引入随机森林、决策树等深度学习算法，优化聚类重叠问题，提升分类精度。
3. 维度层面：增加评估对象的社会背景、生活习惯等特征，丰富评价维度，提升结果全面性。

工具适配说明

1. 国外工具适配：AWS SageMaker国内可正常访问，国内替代品有阿里云PAI、腾讯TI-ONE，功能与适配性相近；Neo4j国内可访问，替代品有NebulaGraph，更适配国内数据存储需求。
2. 应急修复服务：提供24小时响应“代码运行异常”求助，针对本文模型代码的调试效率较自行排查提升40%，可快速解决变量报错、可视化异常等问题。

附录（关键代码节选）

1. PCA主成分分析代码（MATLAB改写）

% 量表数据PCA降维
psych_data = []; % 省略：导入原始量表数据
[m,n] = size(psych_data);
% 数据中心化
data_centered = zeros(m,n);
for i = 1:n
 data_centered(:,i) = psych_data(:,i) - mean(psych_data(:,i));
end
% 计算协方差矩阵并降维
C = cov(data_centered);
[V,D] = eig(C);
E = diag(D);
[u,v] = sort(E,'descend');
V = V(:,v);
k = 2; % 保留2个主成分
X_pca = psych_data * V(:,1:k); % 降维后数据
fprintf('降维后的二维特征数据:\n');
disp(X_pca);

2. 熵权TOPSIS法核心代码（MATLAB改写）

% 熵权TOPSIS法计算综合得分
X = []; % 省略：导入标准化后的量表数据
[n,m] = size(X);
% 计算信息熵
e = zeros(1,m);
for j = 1:m
 p = X(:,j)/sum(X(:,j));
 e(j) = -sum(p.*log(p))/log(n);
end
% 计算权重与综合得分
d = 1 - e;
w = d/sum(d);
% 省略：正理想解、负理想解及距离计算代码
C = D_neg ./ (D_pos + D_neg); % 综合得分
fprintf('各评估对象综合得分:\n');
disp(C);