Stata智慧城市建设对经济高质量发展的影响面板数据分析:超效率SBM模型引入中介变量及空间杜宾模型SDM
从数据科学视角来看,当前我国正处于经济增长模式转型的关键阶段,粗放型增长带来的资源环境问题已逐渐凸显,而智慧城市建设作为数字经济时代的重要抓手,其与经济高质量发展的关联机制亟待通过量化分析厘清。
已分享本文代码和数据资料至会员群
本文内容改编自我们此前为客户完成的一项智慧城市经济影响咨询项目,项目团队通过整合多源统计数据、运用主流计量分析工具,系统探索了智慧城市建设对经济高质量发展的作用路径。
在咨询过程中,我们发现传统研究多聚焦智慧城市对经济增长的直接影响,却较少从绿色全要素生产率(GTFP)视角切入,也缺乏对开放、创新等中介机制及区域异质性的深入探讨。基于此,本研究选取2013-2022年我国30个省份(不含西藏、港澳台地区)的面板数据,采用超效率SBM模型测度经济高质量发展水平,通过固定效应模型、中介效应模型及空间杜宾模型(SDM),层层验证智慧城市建设的经济效应、作用机制与空间溢出特征。
研究不仅为地方政府制定智慧城市发展政策提供了数据支撑,也为理解数字技术驱动经济转型提供了新的分析框架。专题项目文件已分享在交流社群,阅读原文进群和500+行业人士共同交流和成长。
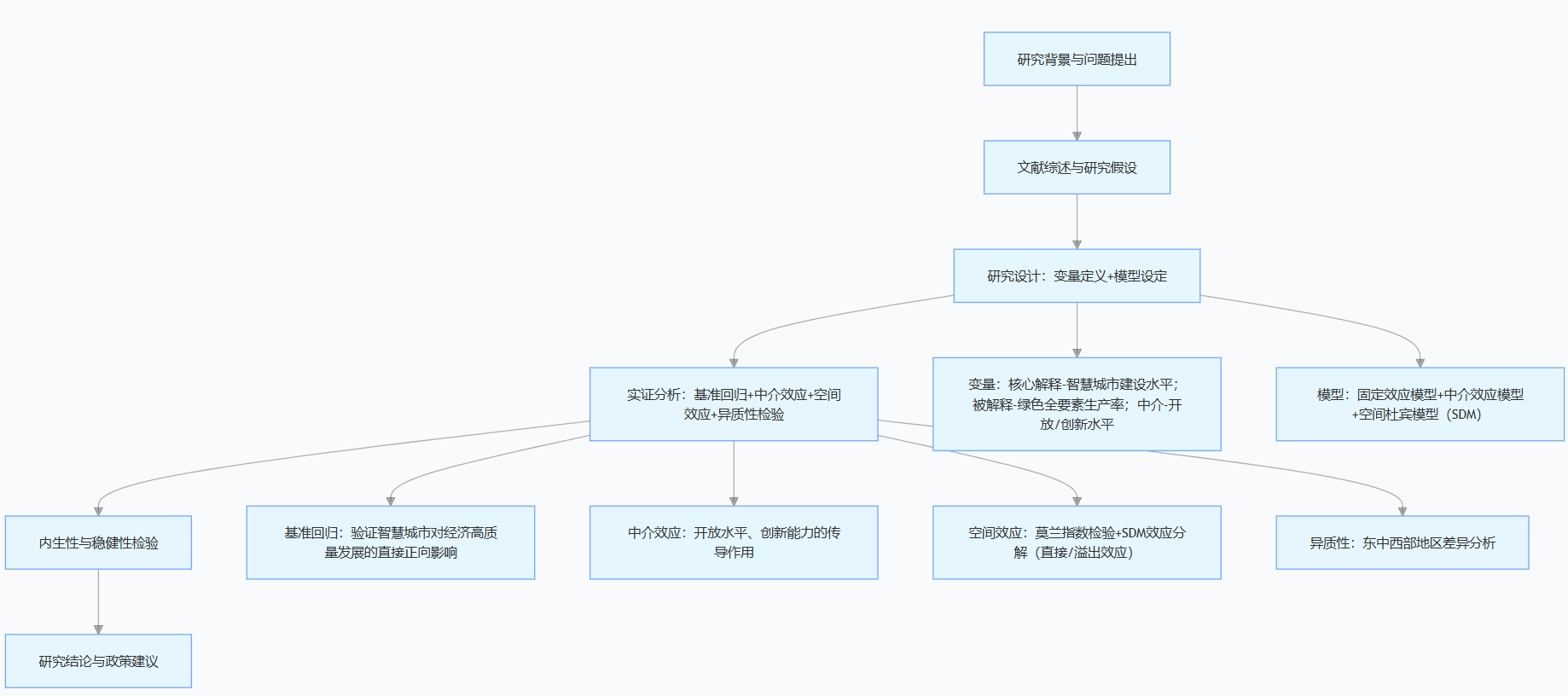
文章脉络流程图
项目截图


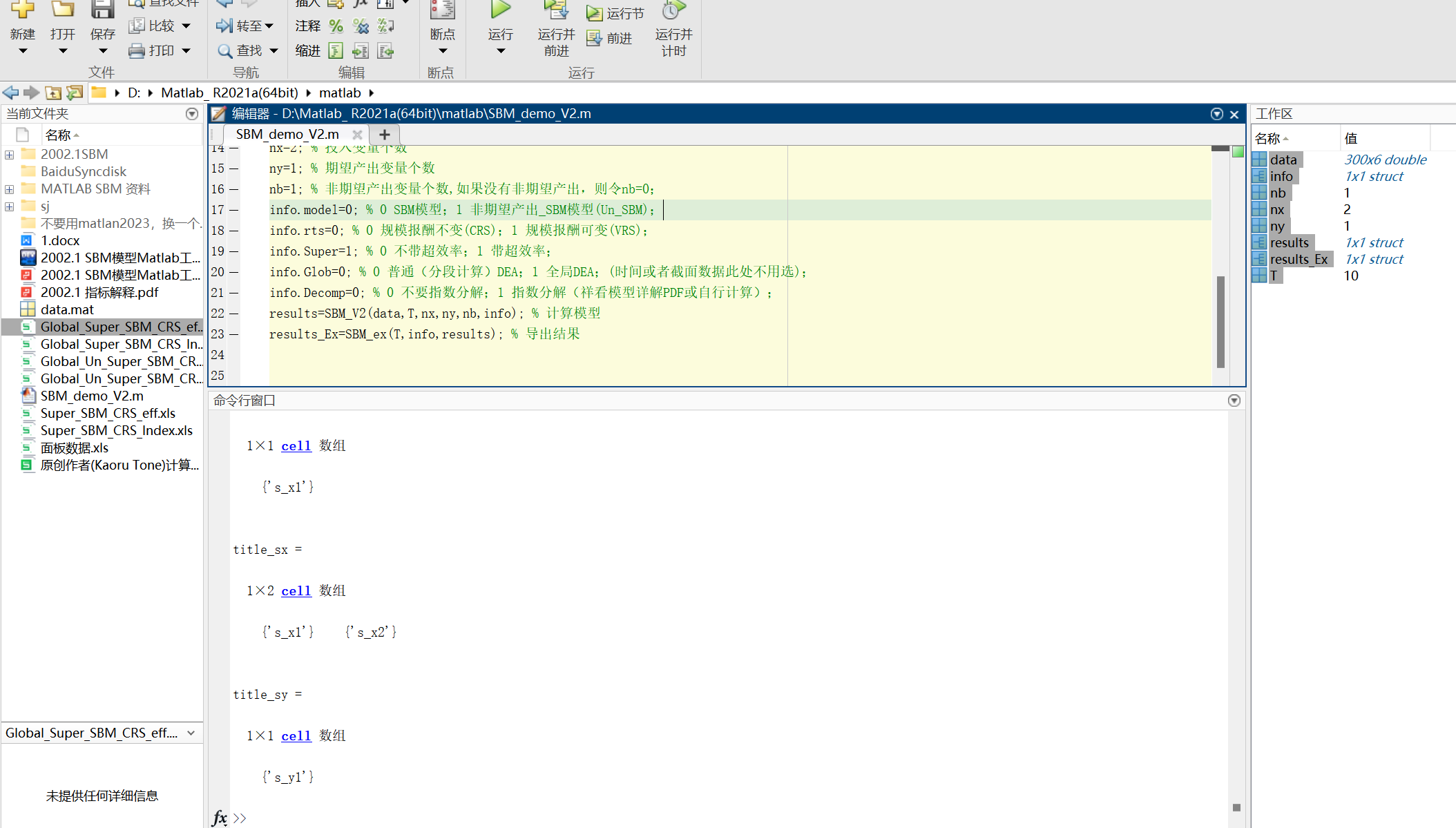
0.绿色全要素生产率超效率模型
1.检验使用固定效应
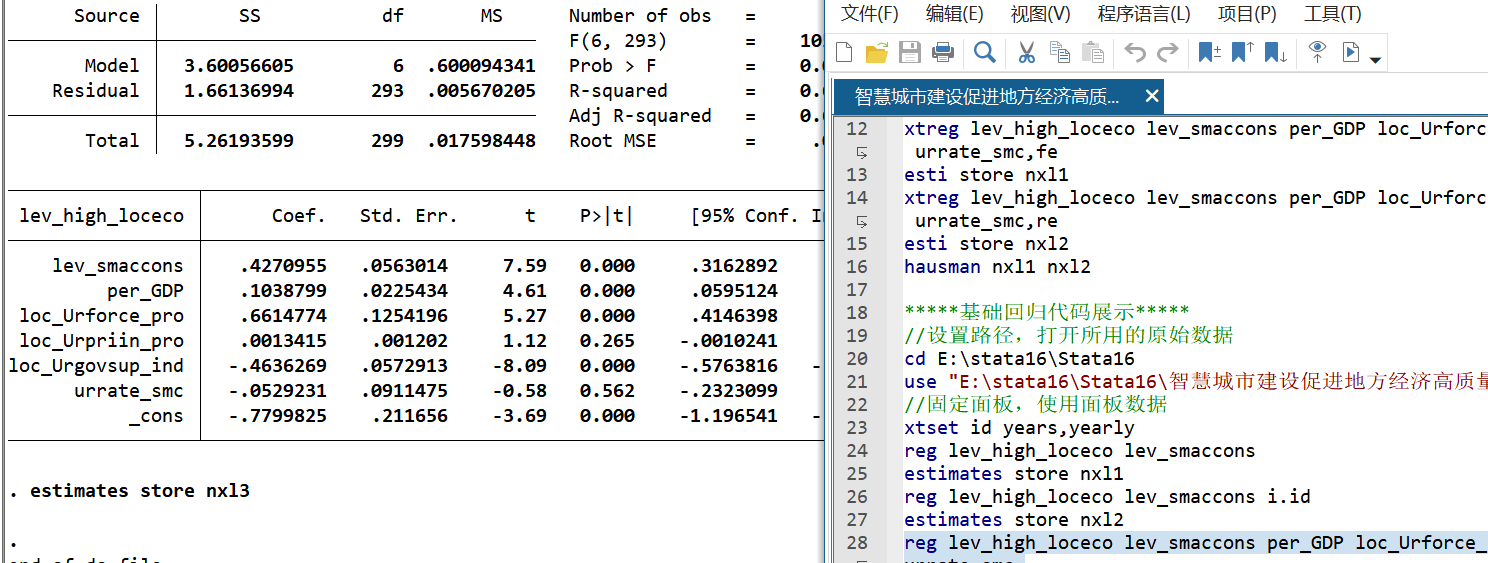
- 基础回归
- 中介1
- 中介2
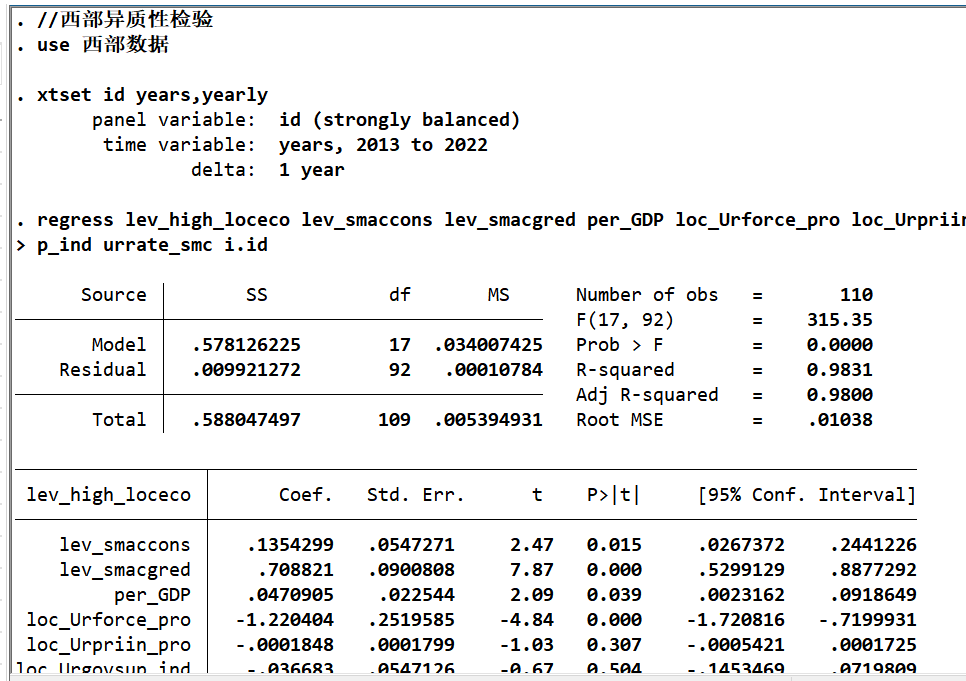
- 异质性检验
- 内生性检验
- 稳定性检验
空间模型
1.全局莫兰指数
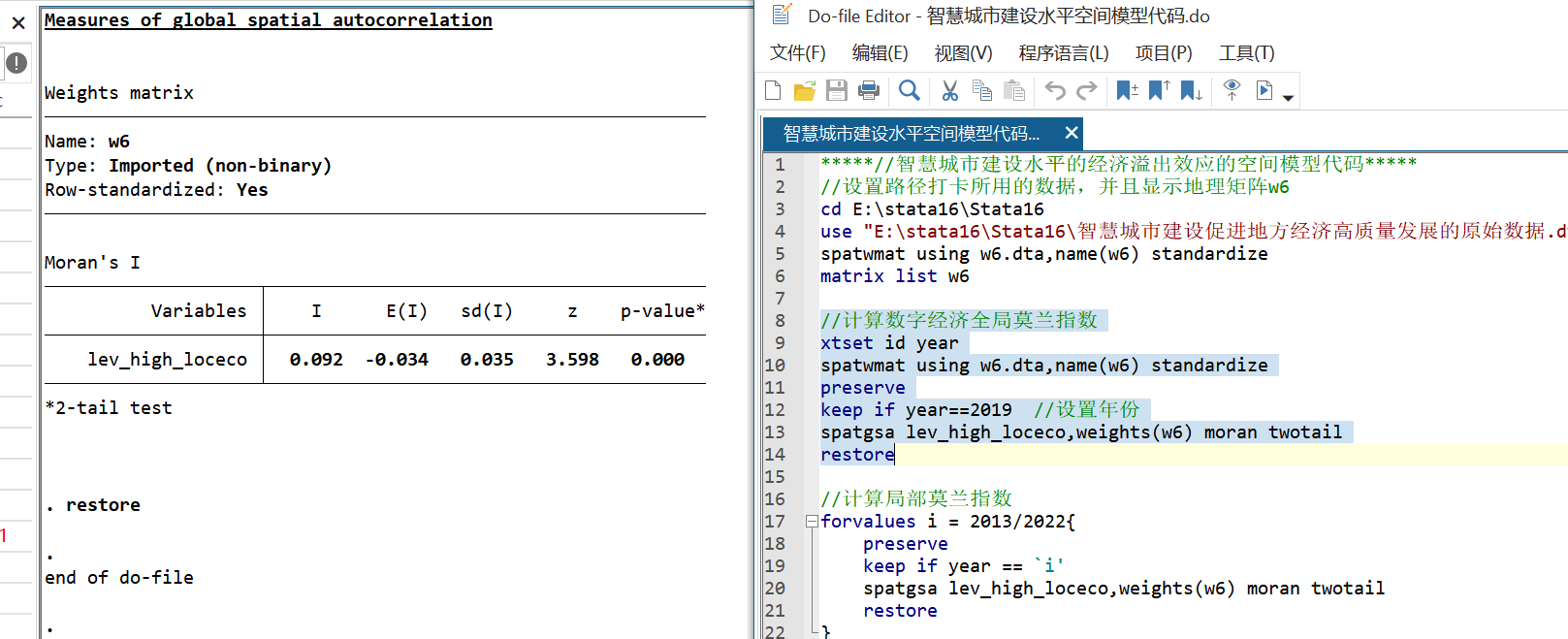
- 局部莫兰指数
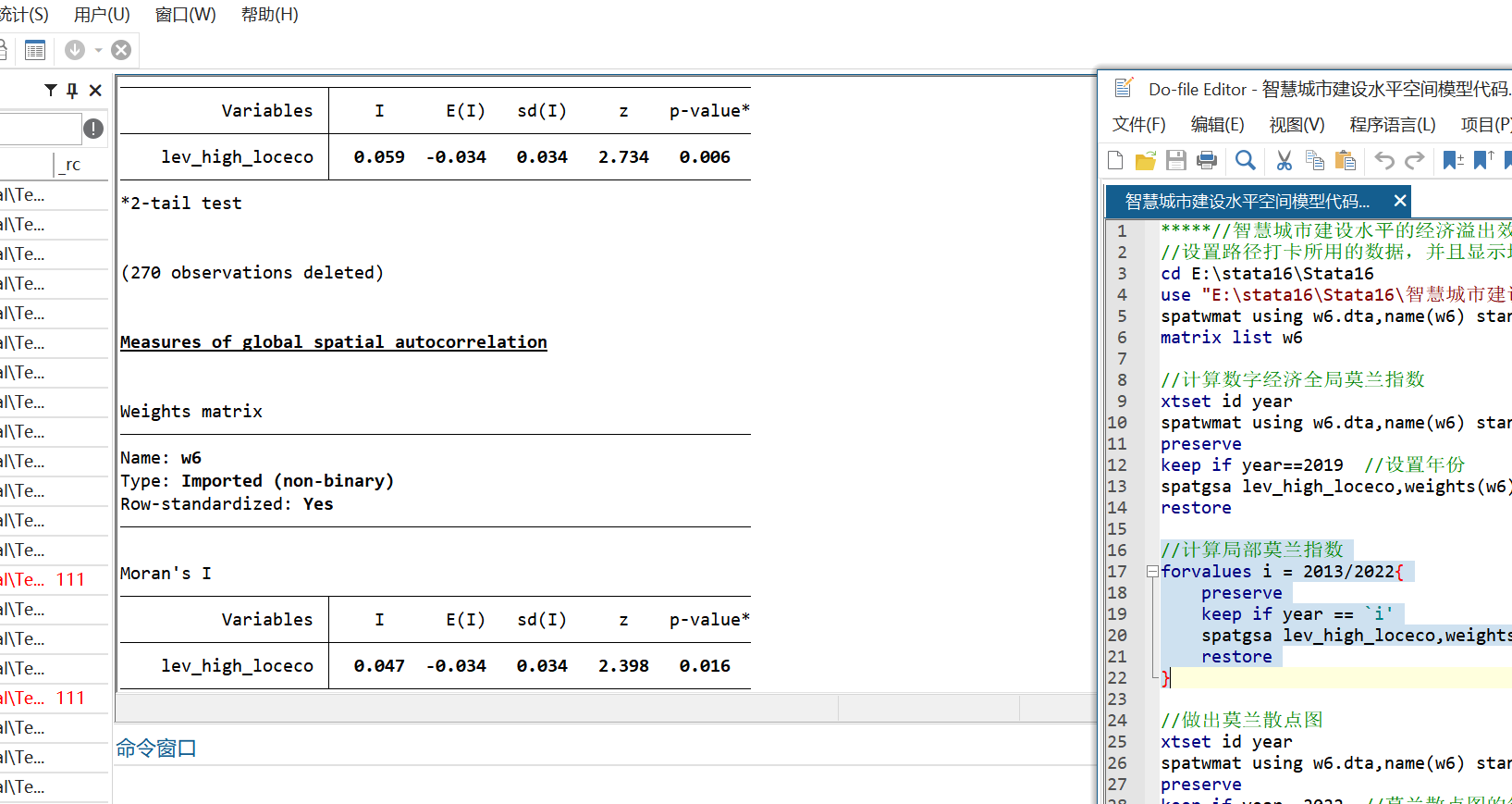
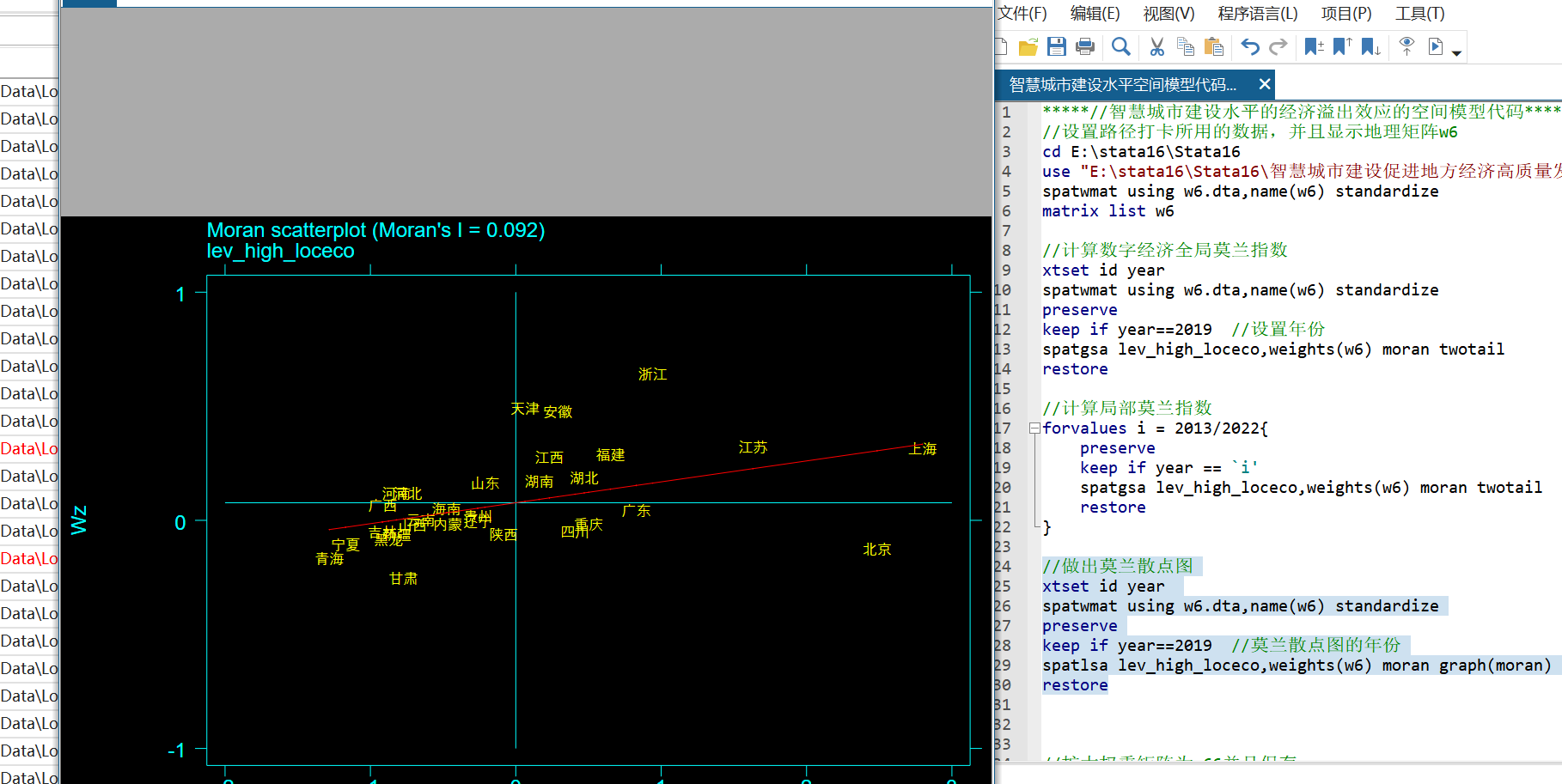
- 莫兰散点图
- 扩大权重矩阵为w66
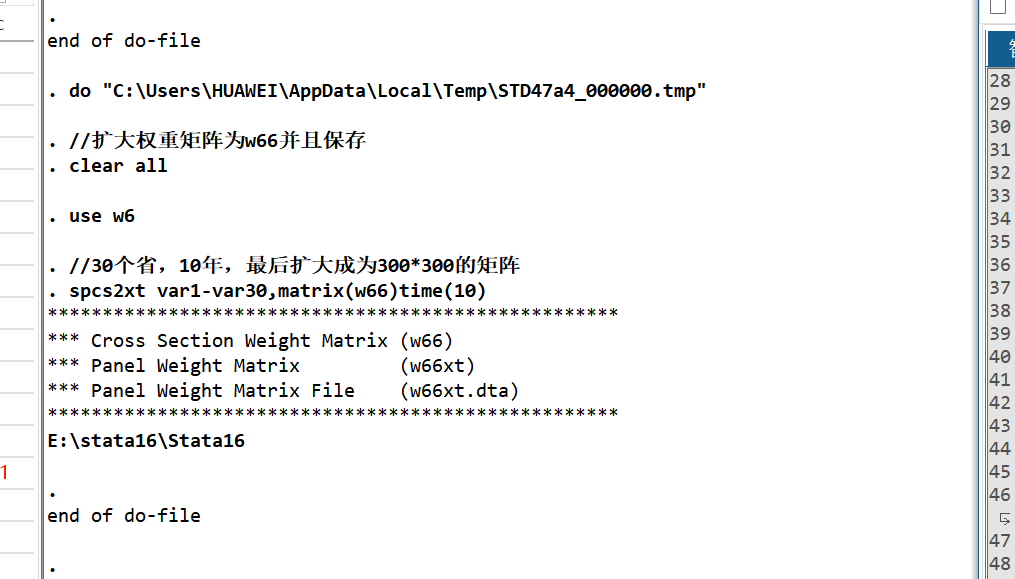
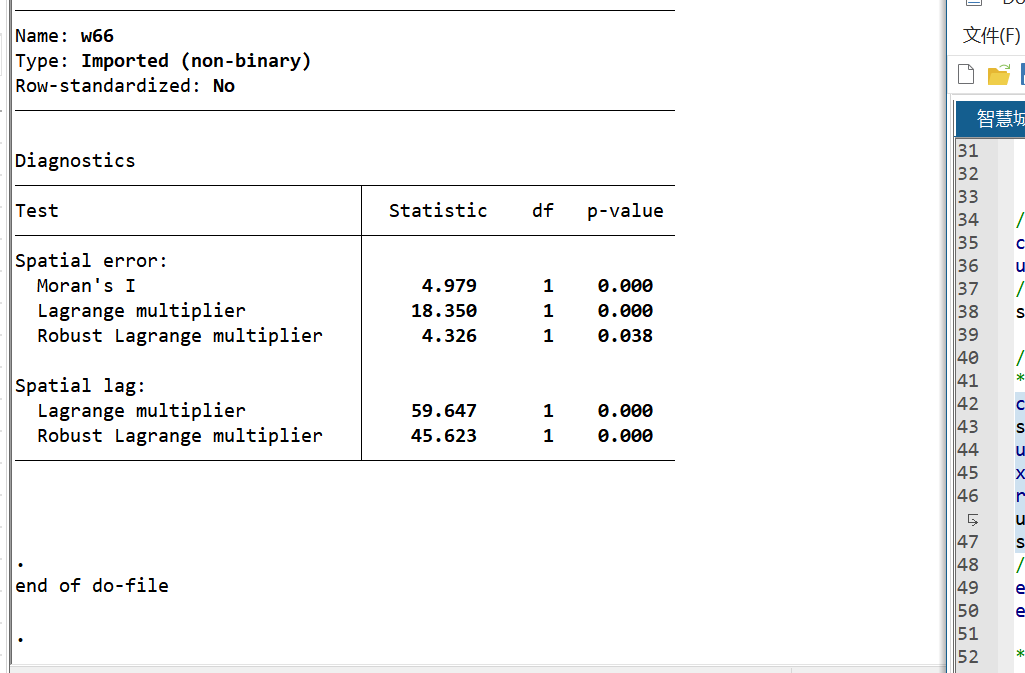
- LM检验,选择误差、滞后或者杜宾模型
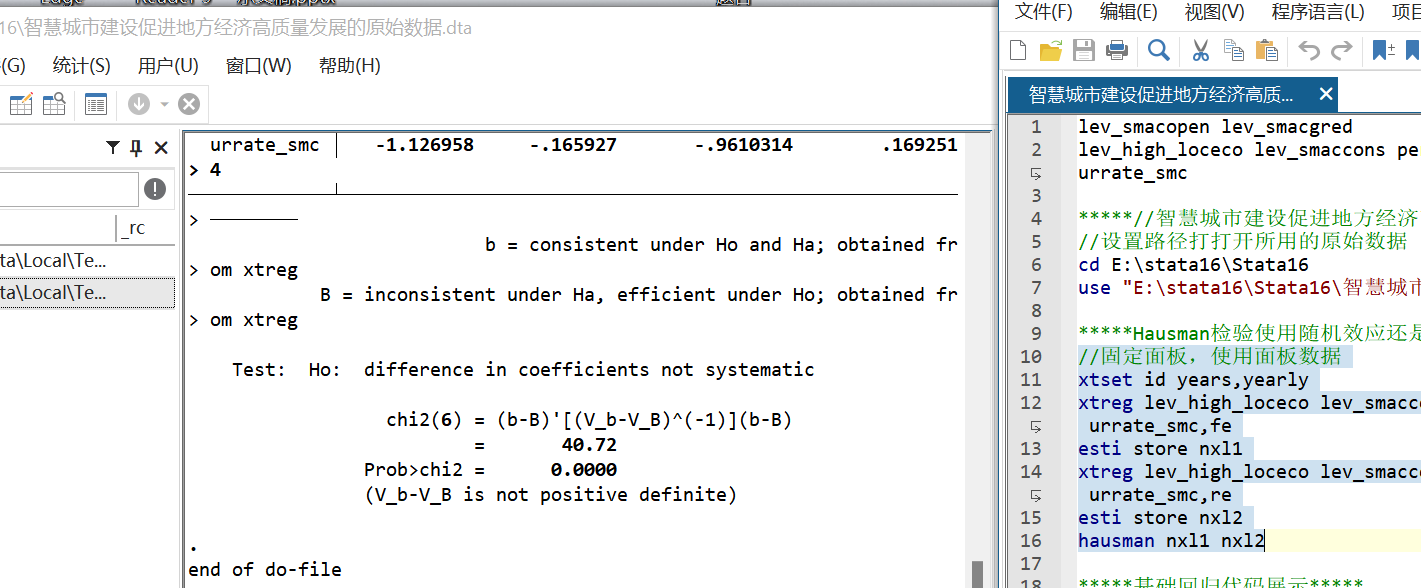
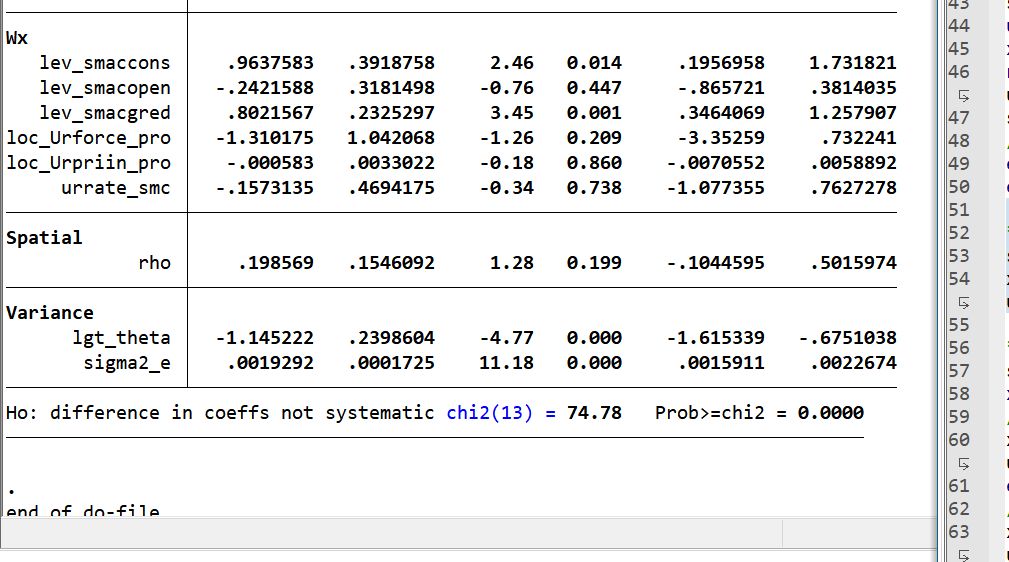
- hausman检验,判断使用固定效应还是随机效应**//显著使用固定
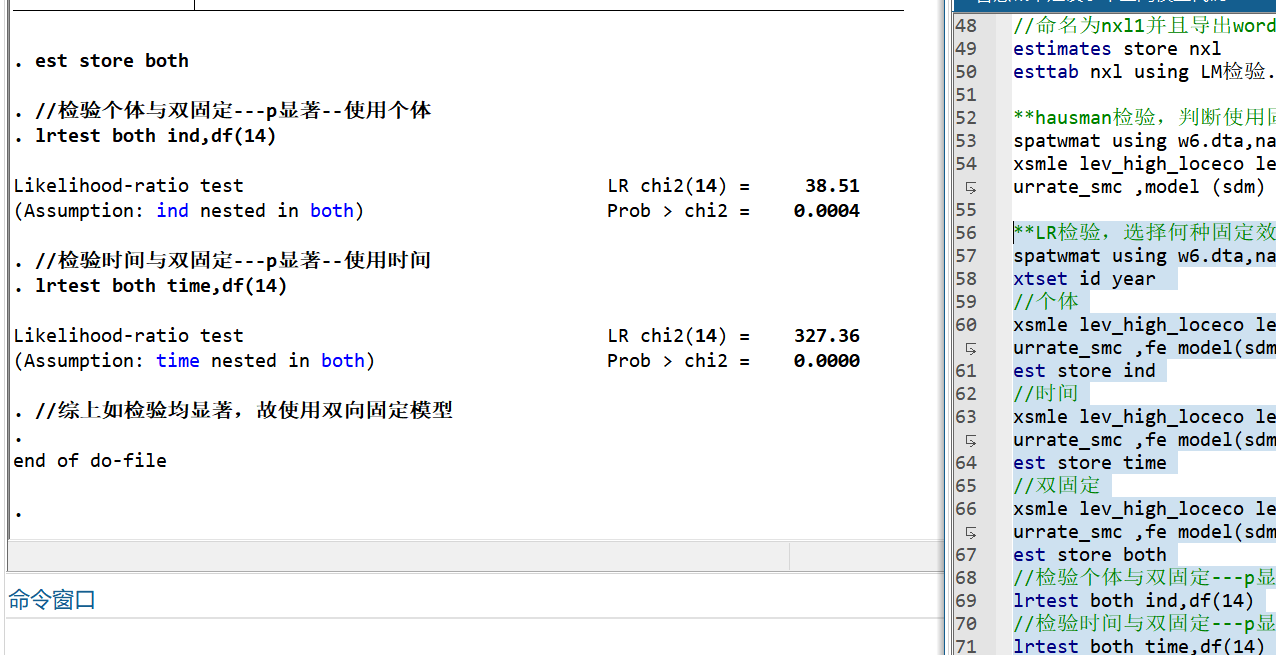
- LR检验,选择何种固定效应
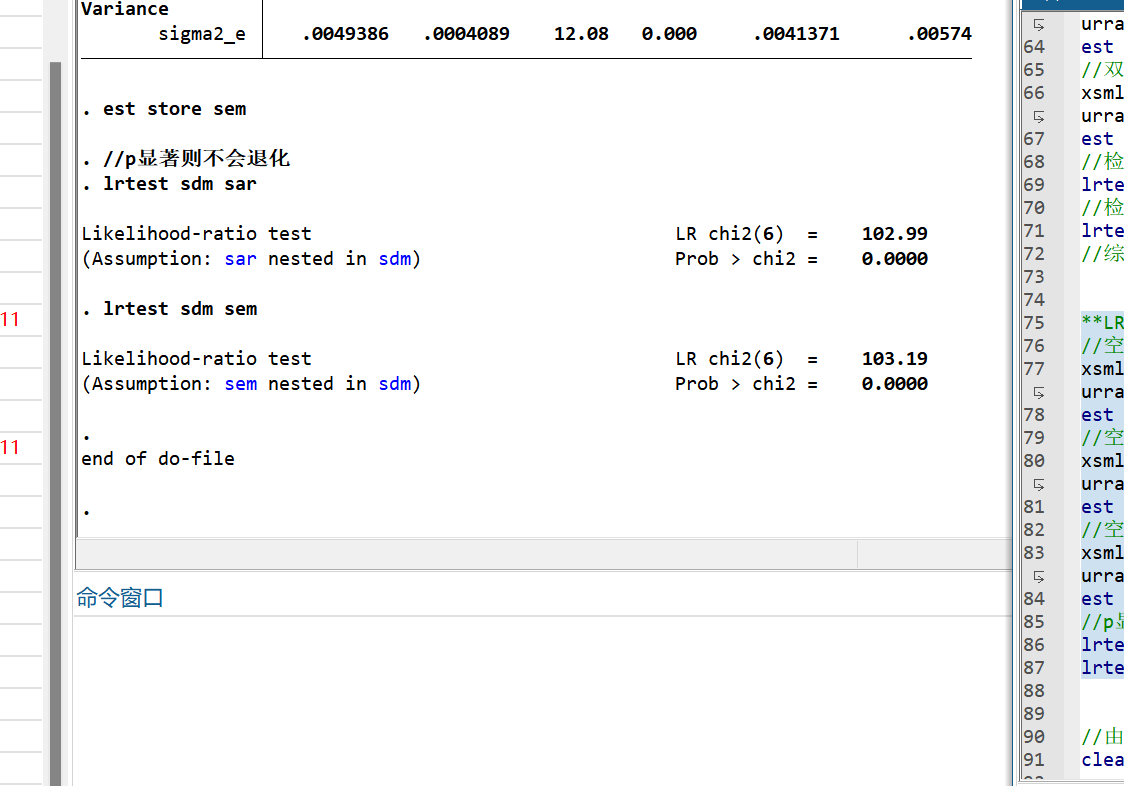
- LR检验是否发出退化效应
- 由运算结果得出本文使用双固定的空间杜量模型
文献综述与研究假设
文献综述核心要点
- 智慧城市概念演进:我国智慧城市经历“数字城市→智慧城市→新型智慧城市”两次升级,2015年后“新型智慧城市”强调以大数据、云计算等技术构建现代化城市体系,契合“创新、协调、绿色、开放、共享”发展理念。
- 现有研究局限:国内外研究多集中于智慧城市对创新、经济增长的宏观影响,缺乏对“绿色全要素生产率”这一高质量发展核心指标的关注,也未深入验证开放水平的传导作用及空间溢出的区域差异。
研究假设
结合理论分析与实践观察,本研究提出以下假设:
- H1:智慧城市建设能显著促进地方经济高质量发展(以绿色全要素生产率衡量)。
- H1a:智慧城市建设通过驱动创新能力提升,间接促进经济高质量发展(创新能力为中介变量)。
- H1b:智慧城市建设通过提高城市开放水平,间接促进经济高质量发展(开放水平为中介变量)。
- H2:智慧城市建设对邻近城市经济高质量发展存在显著正向溢出效应。
研究设计
1. 数据与变量定义
数据来源
选取2013-2022年我国30个省份面板数据,数据均来自《中国统计年鉴》及各省地方统计年鉴,确保数据的权威性与一致性。
核心变量定义
| 变量类型 | 变量名称 | 衡量方法 | 单位 |
|---|---|---|---|
| 被解释变量 | 经济高质量发展水平 | 超效率SBM模型测度的绿色全要素生产率(GTFP),纳入非期望产出(SO₂等) | – |
| 核心解释变量 | 智慧城市建设水平 | 熵权法计算,指标含基础公共服务投入、5G基站密度、科技支出占比等7项二级指标 | – |
| 中介变量 | 城市开放水平 | 外贸依存度(进出口总额/GDP)、实际外商投资额/GDP | 美元/美元 |
| 中介变量 | 城市创新水平 | 科技支出、每万人专利申请量 | 万亿、件 |
| 控制变量 | 人均GDP、劳动力占比等 | 人均地区生产总值、地方城市劳动力占比、第一产业占比等 | 万元、%等 |
2. 模型设定
(1)基准回归模型(固定效应)
为验证H1,设定固定效应模型如下:
lev_high_loceco(it) = α0 + α1*lev_smaccons(it) + α2*control(it) + μi + vt + ε(it)
- 其中:i为省份,t为年份;lev_high_loceco为经济高质量发展水平;lev_smaccons为智慧城市建设水平;control为控制变量;μi为省份固定效应;vt为年份固定效应;ε为随机扰动项。
- 经Hausman检验(chi2=40.72,Prob>chi2=0.0000),拒绝随机效应假设,选用固定效应模型。
(2)中介效应模型
为验证H1a、H1b,参考温忠麟中介效应检验方法,构建以下模型:
- 开放水平中介:
lev_smacopen(it) = β0 + β1*lev_smaccons(it) + β2*control(it) + μi + vt + ε(it)
lev_high_loceco(it) = γ0 + γ1*lev_smaccons(it) + γ2*lev_smacopen(it) + γ3*control(it) + μi + vt + ε(it) - 创新水平中介:
lev_smacrea(it) = δ0 + δ1*lev_smaccons(it) + δ2*control(it) + μi + vt + ε(it)
lev_high_loceco(it) = θ0 + θ1*lev_smaccons(it) + θ2*lev_smacrea(it) + θ3*control(it) + μi + vt + ε(it)
(3)空间杜宾模型(SDM)
为验证H2,先通过莫兰指数检验空间自相关性,再构建SDM模型:
lev_high_loceco(it) = ρ*W*lev_high_loceco(it) + β*lev_smaccons(it) + θ*W*lev_smaccons(it) + X(it)*γ + μi + vt + ε(it)
- W为地理距离权重矩阵(Wij=1/dij,dij为省份i与j的直线距离);ρ为空间自回归系数;θ为解释变量空间滞后项系数;X为控制变量矩阵。
实证分析
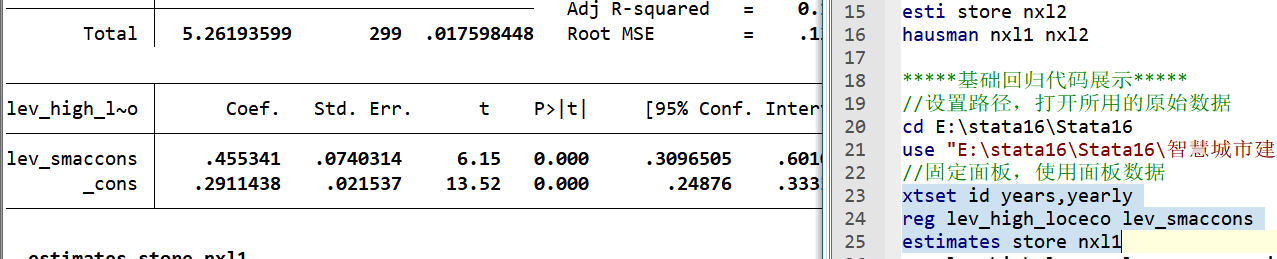
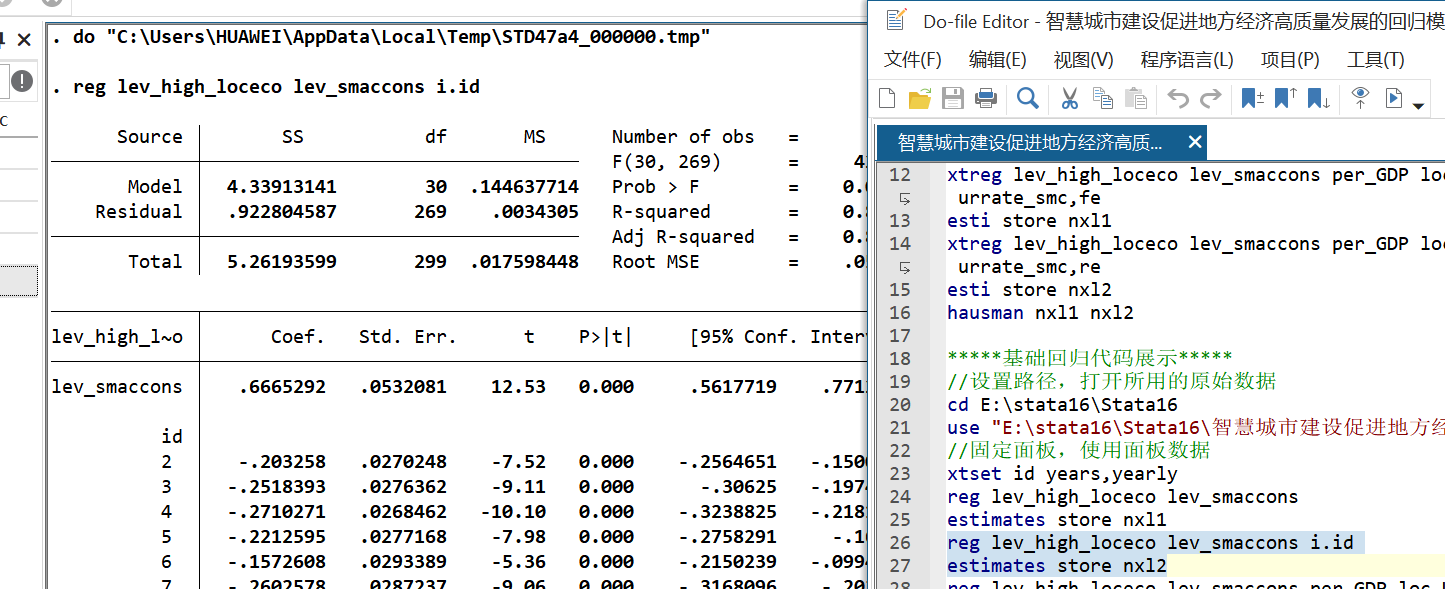
1. 基准回归结果
通过固定效应模型分析,结果如下表所示:
| 变量 | (1)无控制变量(混合回归) | (2)控制省份固定效应 | (3)控制省份+控制变量 | (4)双固定效应(省份+年份) |
|---|---|---|---|---|
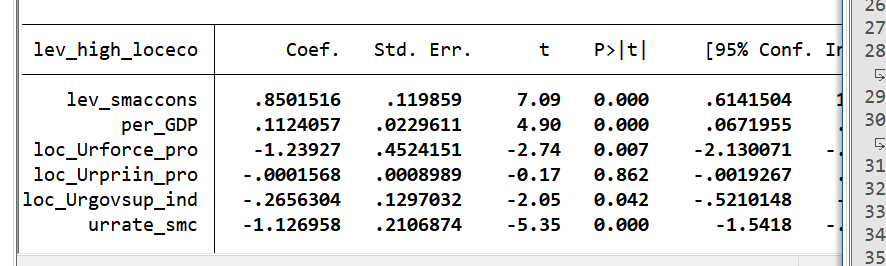
| lev_smaccons | 0.455***(6.15) | 0.667***(12.53) | 0.427***(7.59) | 0.850***(7.09) |
| 控制变量 | NO | NO | YES | YES |
| N | 300 | 300 | 300 | 300 |
| R-sq | 0.11 | 0.82 | 0.86 | 0.68 |
结论:无论是否加入控制变量与固定效应,智慧城市建设水平(lev_smaccons)系数均在1%水平显著为正,说明智慧城市建设对经济高质量发展存在直接正向促进作用,H1成立。
2. 中介效应分析
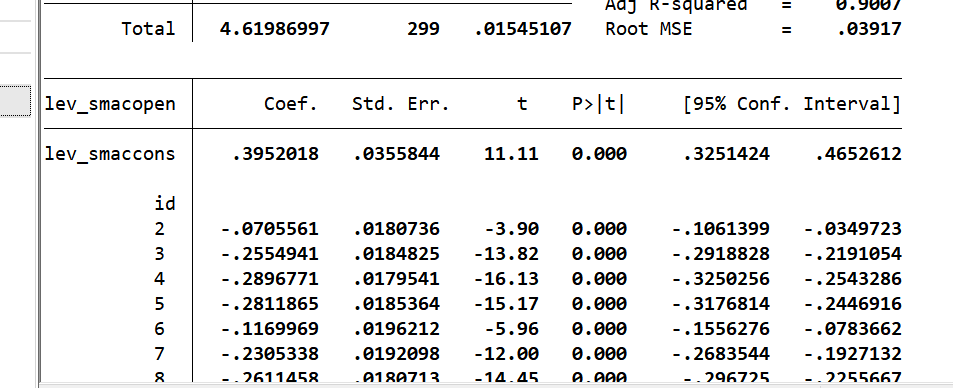
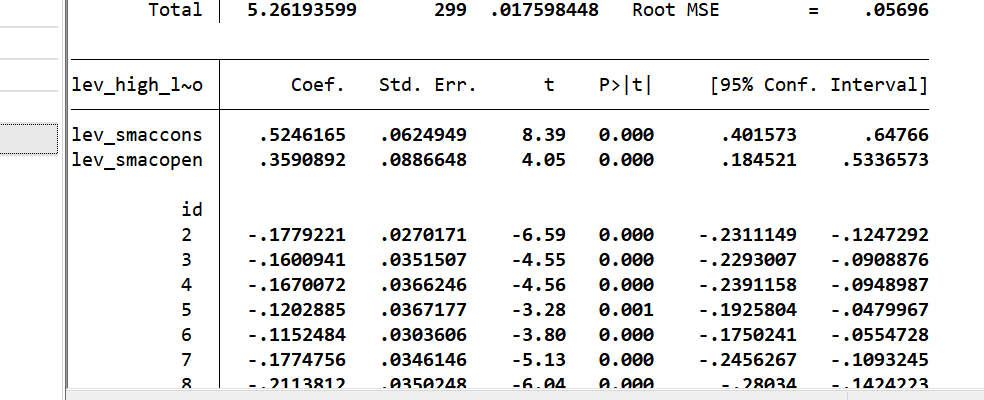
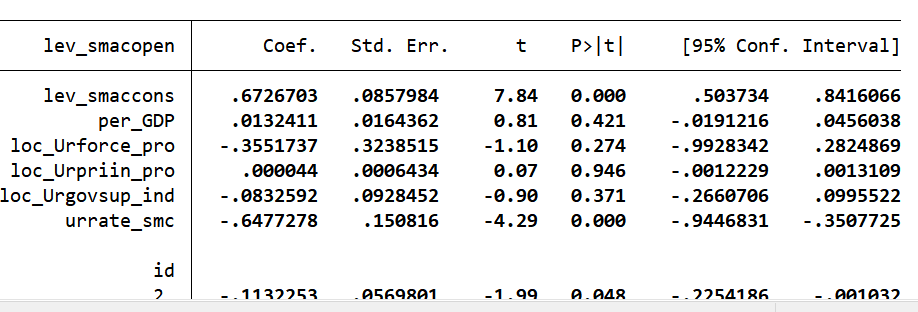
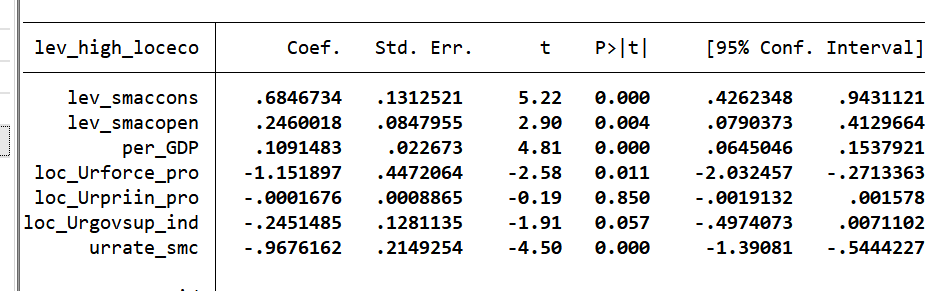
(1)开放水平中介(验证H1b)
| 变量 | (1)开放水平(lev_smacopen) | (2)经济高质量发展 | (3)开放水平(加控制变量) | (4)经济高质量发展(加控制变量) |
|---|---|---|---|---|
| lev_smaccons | 0.395***(11.11) | 0.525***(8.39) | 0.673***(7.84) | 0.685***(5.22) |
| lev_smacopen | – | 0.359***(4.05) | – | 0.246**(2.90) |
| 控制变量 | NO | NO | YES | YES |
| N | 300 | 300 | 300 | 300 |
| R-sq | 0.91 | 0.83 | 0.92 | 0.86 |
结论:lev_smaccons对开放水平系数显著为正,且开放水平对经济高质量发展系数也显著为正,说明开放水平是中介变量,H1b成立。
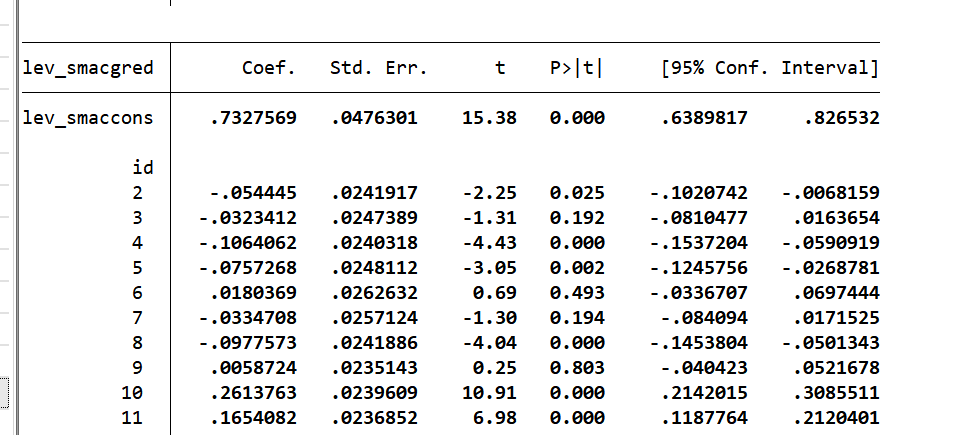
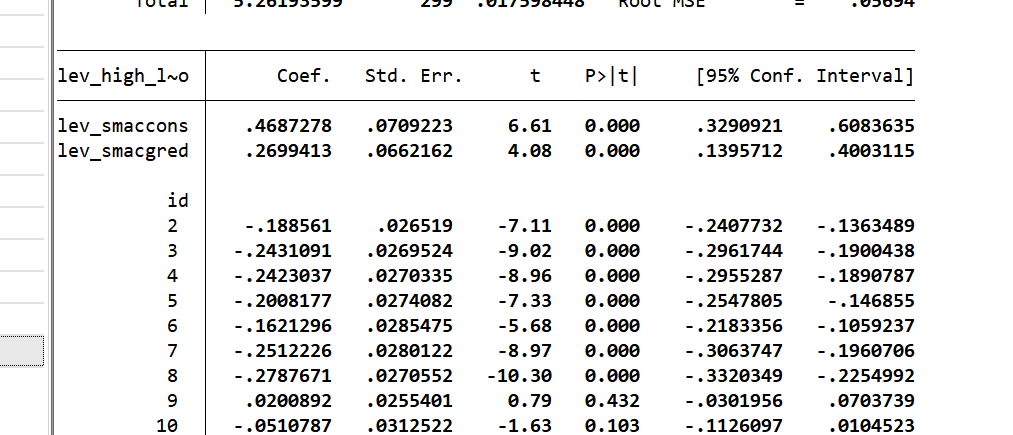
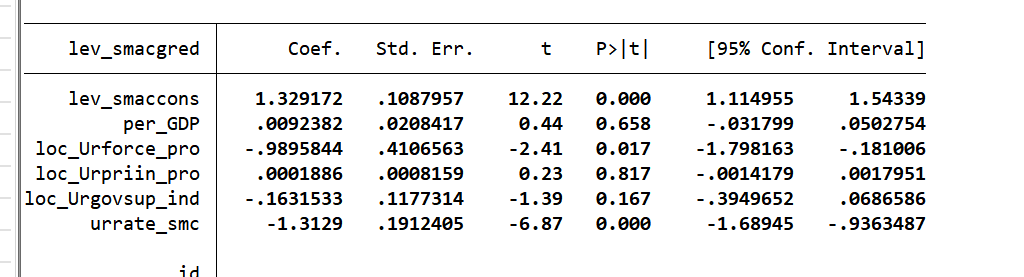
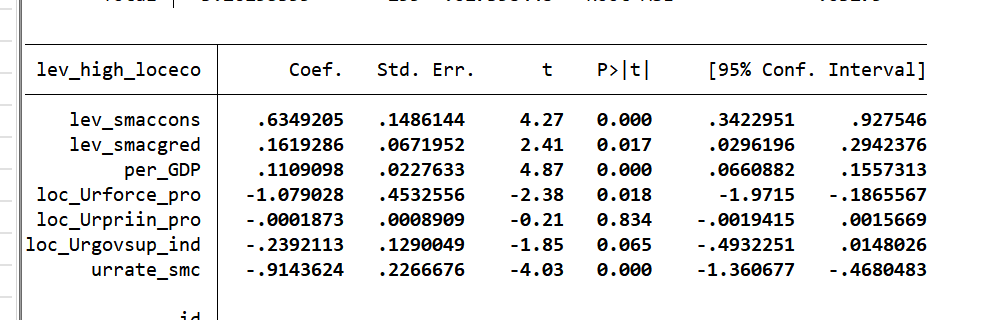
(2)创新水平中介(验证H1a)
| 变量 | (1)创新水平(lev_smacrea) | (2)经济高质量发展 | (3)创新水平(加控制变量) | (4)经济高质量发展(加控制变量) |
|---|---|---|---|---|
| lev_smaccons | 0.733***(15.38) | 0.469***(6.61) | 1.329***(12.22) | 0.635***(4.27) |
| lev_smacrea | – | 0.270***(4.08) | – | 0.162*(2.41) |
| 控制变量 | NO | NO | YES | YES |
| N | 300 | 300 | 300 | 300 |
| R-sq | 0.89 | 0.83 | 0.90 | 0.86 |
结论:lev_smaccons对创新水平系数显著为正,且创新水平对经济高质量发展系数显著为正,说明创新水平是中介变量,H1a成立。
3. 空间效应分析
(1)空间自相关性检验(莫兰指数)
通过Stata计算2013-2022年莫兰指数(Moran’s I),结果如下表所示(选取部分年份):
| 年份 | Moran’s I | z值 | p值 |
|---|---|---|---|
| 2013 | 0.112 | 4.013 | 0.000 |
| 2016 | 0.106 | 3.885 | 0.000 |
| 2019 | 0.092 | 3.598 | 0.000 |
| 2022 | 0.047 | 2.398 | 0.016 |
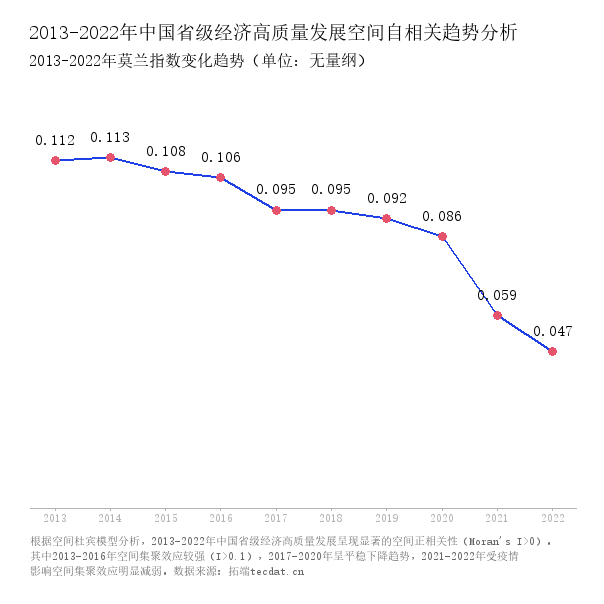
所有年份Moran’s I均为正且通过5%显著性检验,说明经济高质量发展存在空间正相关。以下为部分年份莫兰散点图:
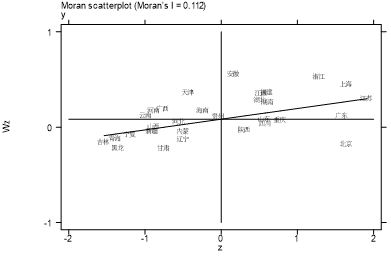
散点图中多数点分布于第一、三象限,呈现“高-高”“低-低”聚集模式,进一步验证空间正相关。
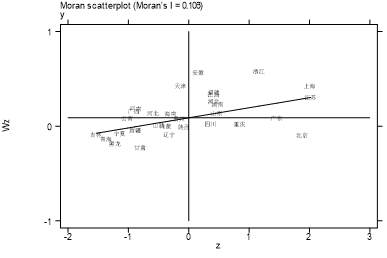
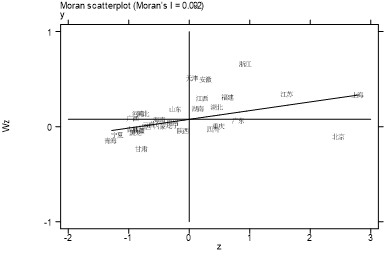
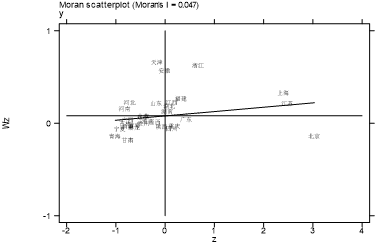
(2)空间杜宾模型效应分解
经LM检验(拒绝无空间依赖)、LR检验(拒绝退化为空间误差/滞后模型),最终选用双固定效应SDM,效应分解结果如下:
| 变量 | 直接效应 | 溢出效应(间接效应) | 总效应 |
|---|---|---|---|
| lev_smaccons | 0.603*** | 2.025*** | 2.628*** |
| 显著性(p值) | <0.001 | <0.001 | <0.001 |
结论:智慧城市建设对本地经济高质量发展直接效应显著(0.603),对邻近城市溢出效应更显著(2.025),H2成立。
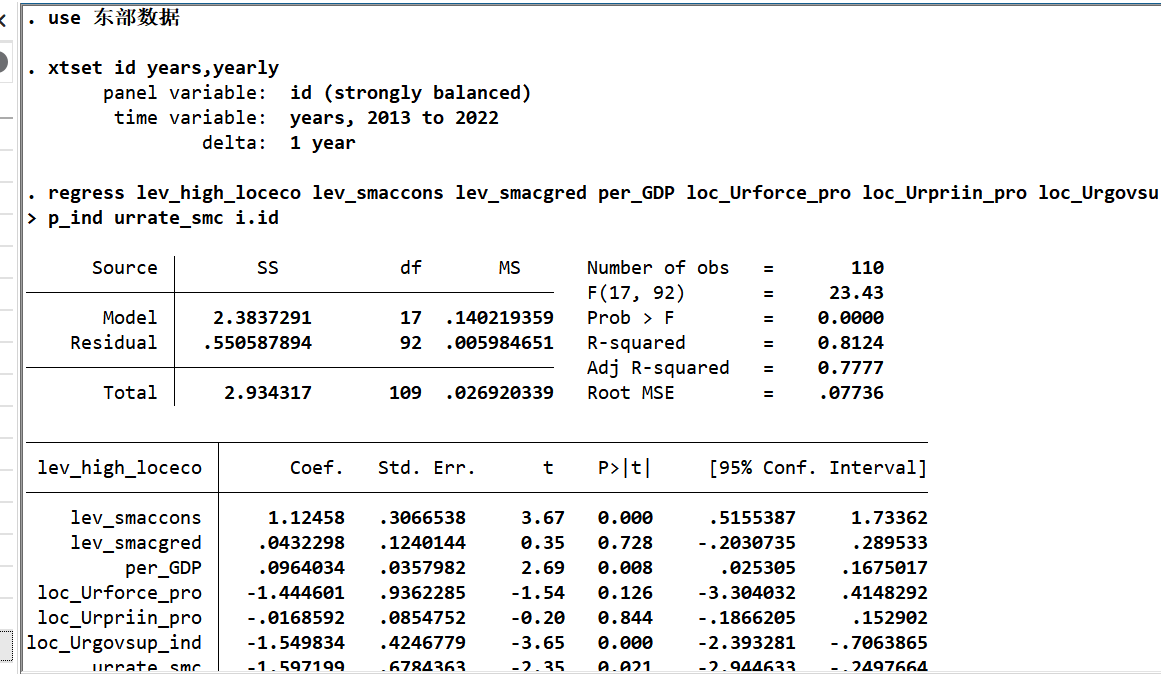
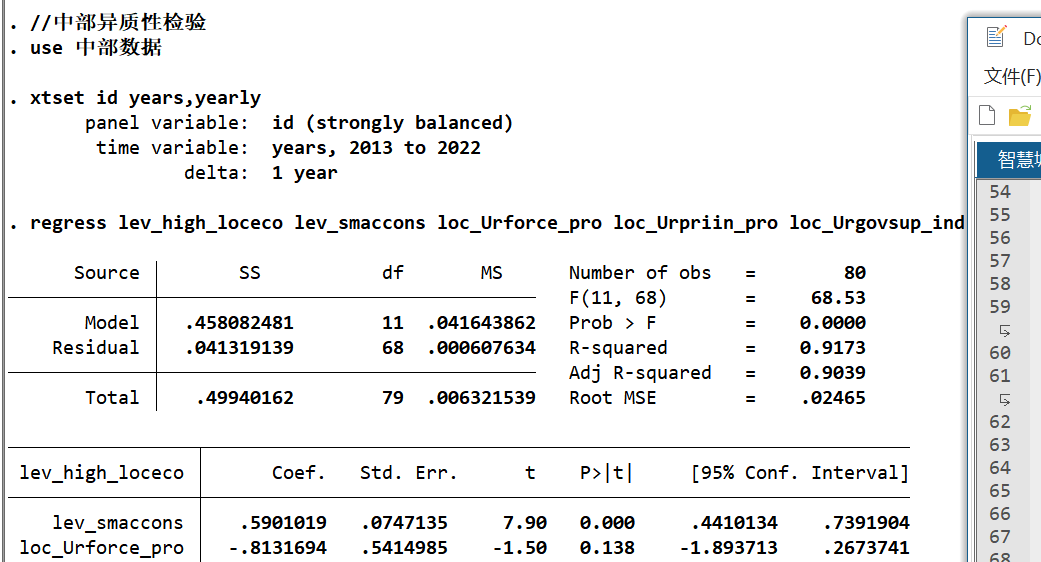
4. 区域异质性分析
将30个省份分为东、中、西三区域,检验智慧城市建设的区域差异:
| 变量 | 东部地区 | 中部地区 | 西部地区 |
|---|---|---|---|
| lev_smaccons | 1.183***(4.63) | 0.590***(7.90) | 0.183*(2.61) |
| N | 110 | 80 | 110 |
| R-sq | 0.82 | 0.82 | 0.97 |
结论:智慧城市建设对东、中、西部均有促进作用,但东部(1.183)>中部(0.590)>西部(0.183),差异源于东部经济基础好、技术人才集中,西部则受基础设施与人才限制。
5. 内生性与稳健性检验
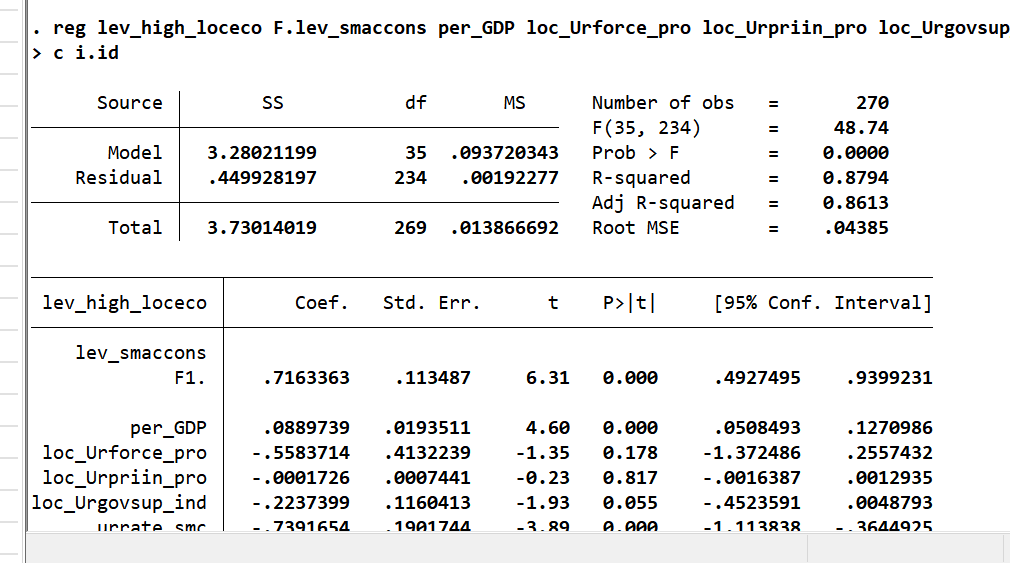
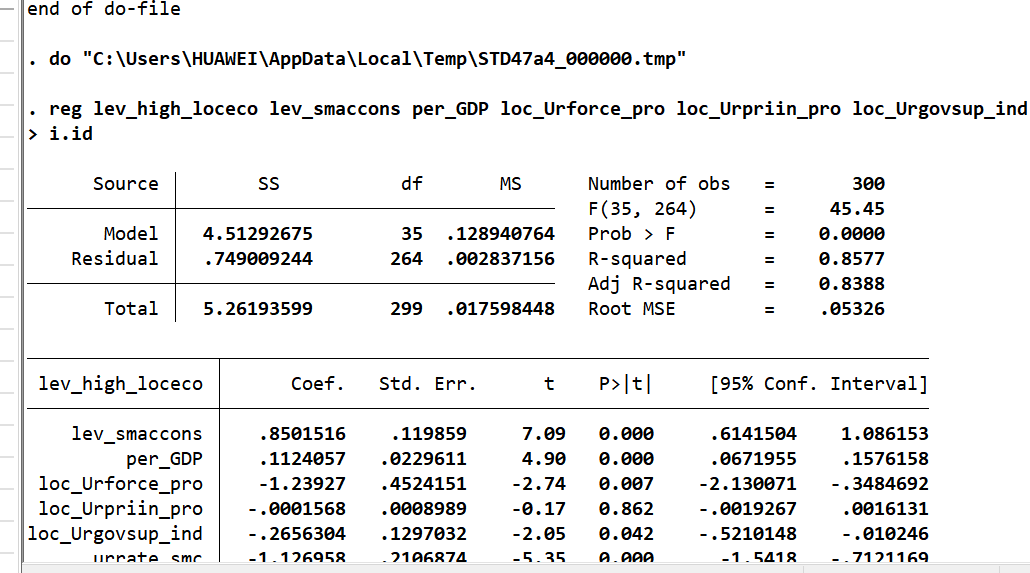
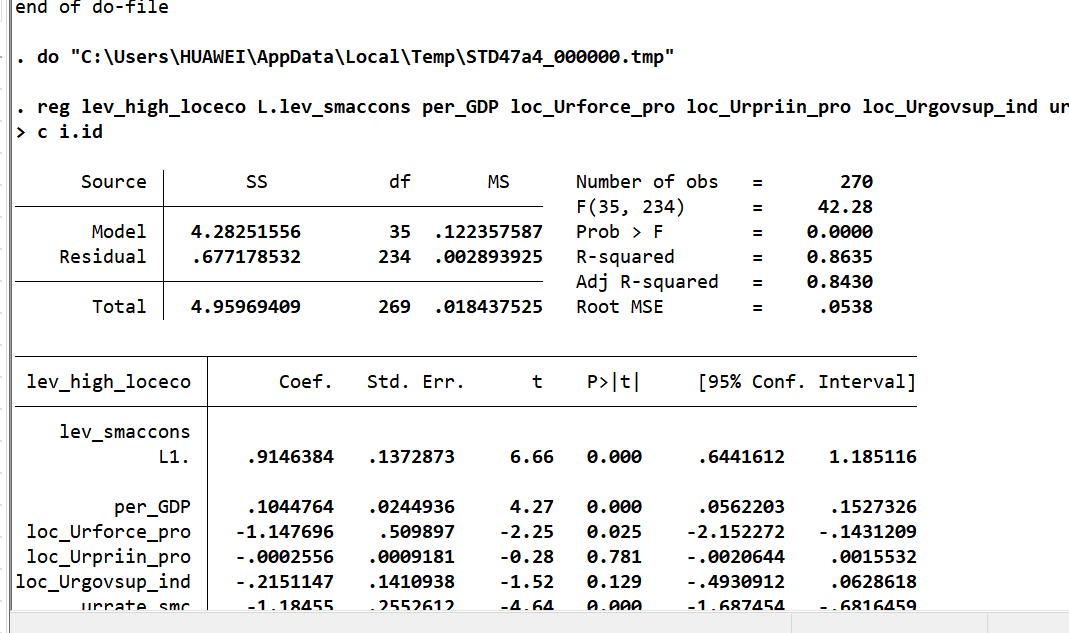
(1)内生性检验(滞后/提前一期)
| 变量 | 提前一年(F.lev_smaccons) | 标准模型(lev_smaccons) | 滞后一年(L.lev_smaccons) |
|---|---|---|---|
| 系数(t值) | 0.716***(6.31) | 0.850***(7.09) | 0.915***(6.66) |
| N | 270 | 300 | 270 |
| R-sq | 0.86 | 0.84 | 0.84 |
结论:滞后/提前一期系数仍显著为正,排除内生性干扰。
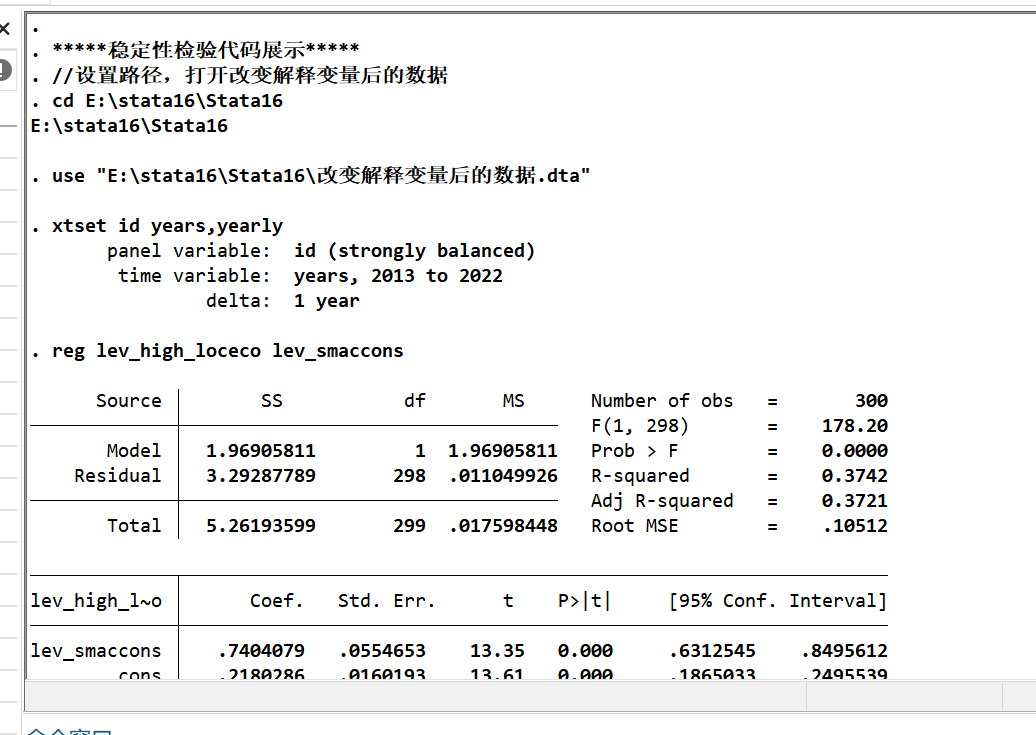
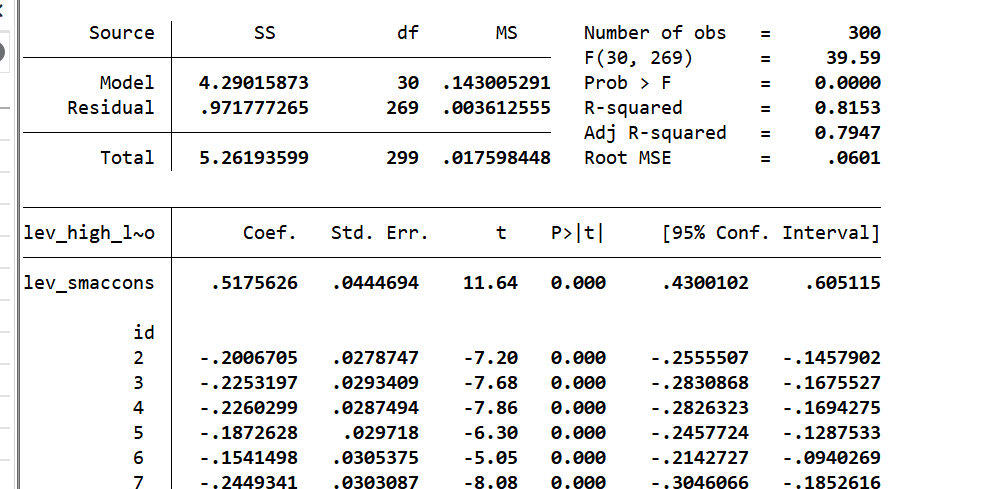
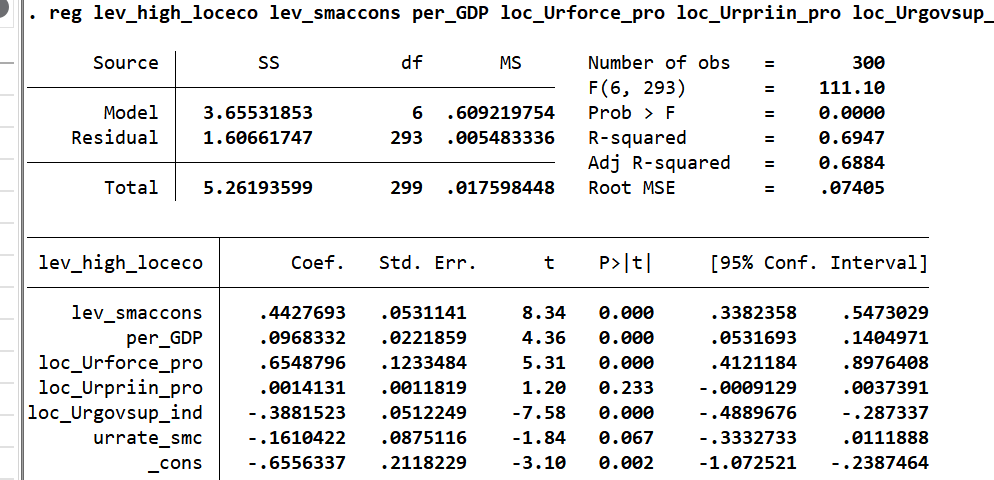
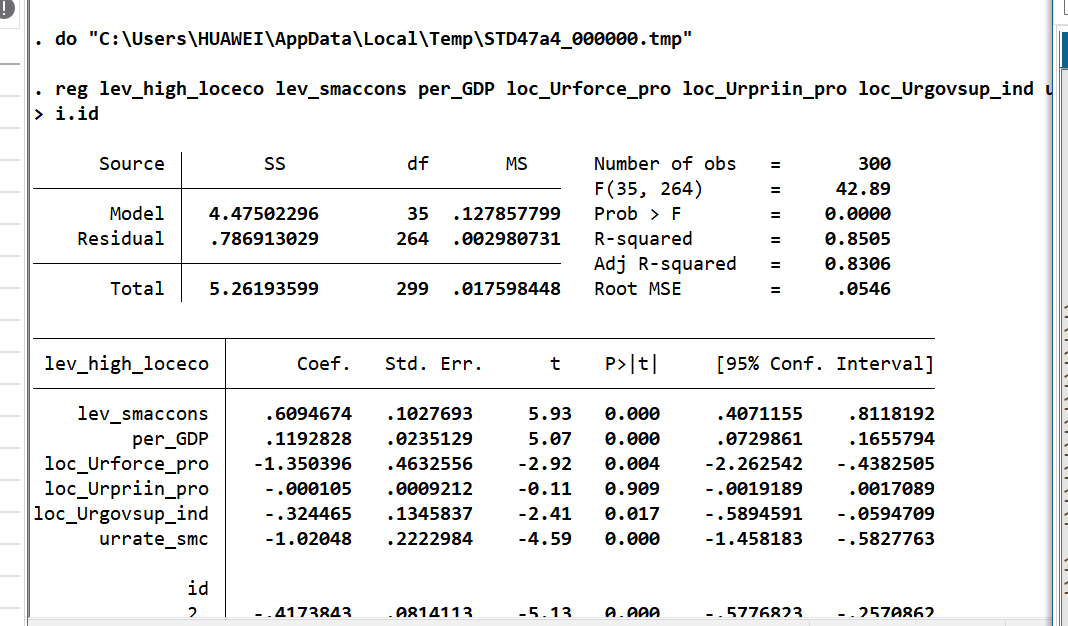
(2)稳健性检验(更换核心解释变量指标)
调整智慧城市建设水平指标(保留5项二级指标),重新计算后回归:
| 变量 | 无控制变量 | 控制省份固定效应 | 控制省份+控制变量 | 双固定效应 |
|---|---|---|---|---|
| G.lev_smaccons | 0.740*** | 0.518*** | 0.443*** | 0.609*** |
| N | 300 | 300 | 300 | 300 |
| R-sq | 0.37 | 0.79 | 0.69 | 0.83 |
结论:核心解释变量更换后仍显著为正,结论稳健。

Stata广义矩量法GMM面板向量自回归PVAR模型选择、估计、Granger因果检验分析投资、收入和消费数据
本文介绍了如何使用Stata进行广义矩量法(GMM)面板向量自回归(PVAR)模型的估计与分析,包括模型选择、Granger因果检验等关键步骤,并通过投资、收入和消费数据展示了实际应用案例。
阅读全文研究结论与政策建议
1. 研究结论
- 直接效应:智慧城市建设通过提升绿色全要素生产率,直接促进经济高质量发展,这一结论经内生性与稳健性检验验证。
- 中介机制:开放水平与创新能力是关键中介,智慧城市通过优化贸易便利化、推动技术创新(如5G、大数据应用),间接助力经济
每日分享最新报告和数据资料至会员群
关于会员群
- 会员群主要以数据研究、报告分享、数据工具讨论为主;
- 加入后免费阅读、下载相关数据内容,并同步海内外优质数据文档;
- 老用户可九折续费。
- 提供报告PDF代找服务
非常感谢您阅读本文,如需帮助请联系我们!



 DeepMTS深度学习多元时间序列分析预测宏观经济指标数据可视化|附数据代码
DeepMTS深度学习多元时间序列分析预测宏观经济指标数据可视化|附数据代码 【专题】2024年中国低空经济报告——蓄势待飞,展翅万亿新赛道报告合集PDF分享(附原数据表)
【专题】2024年中国低空经济报告——蓄势待飞,展翅万亿新赛道报告合集PDF分享(附原数据表) R语言聚类分析、因子分析、主成分分析PCA农村农业相关经济指标数据可视化
R语言聚类分析、因子分析、主成分分析PCA农村农业相关经济指标数据可视化 【专题】2023中国经济高质量发展中的商业地产趋势与机遇专题报告PDF合集分享(附原数据表)
【专题】2023中国经济高质量发展中的商业地产趋势与机遇专题报告PDF合集分享(附原数据表)
