此示例显示如何使用估计复合条件均值和方差模型estimate。
加载工具箱附带的NASDAQ数据 。
对于数值稳定性，将返回值转换为收益率。
可下载资源
指定AR（1）和GARCH（1,1）复合模型。
加载数据并指定模型
一个独立 相同分布的标准化高斯过程。
load Data_EquityIdx
nasdaq = DataTable.NASDAQ;
r = 100*price2ret(nasdaq);
T = length(r);
Mdl = arima('ARLags',1,'Variance',garch(1,1))
Mdl =
arima with properties:
Description: "ARIMA(1,0,0) Model (Gaussian Distribution)"
Distribution: Name = "Gaussian"
P: 1
D: 0
Q: 0
Constant: NaN
AR: {NaN} at lag [1]
SAR: {}
MA: {}
SMA: {}
Seasonality: 0
Beta: [1×0]
Variance: [GARCH(1,1) Model]不使用预采样数据估计模型参数
使用estimate。使用estimate自动生成的预采样观察。
EstMdl = estimate(Mdl,r);
ARIMA(1,0,0) Model (Gaussian Distribution):
Value StandardError TStatistic PValue
________ _____________ __________ __________
Constant 0.072632 0.018047 4.0245 5.7087e-05
AR{1} 0.13816 0.019893 6.945 3.7845e-12
GARCH(1,1) Conditional Variance Model (Gaussian Distribution):
Value StandardError TStatistic PValue
________ _____________ __________ __________
Constant 0.022377 0.0033201 6.7399 1.5852e-11
GARCH{1} 0.87312 0.0091019 95.927 0
ARCH{1} 0.11865 0.008717 13.611 3.4339e-42估计显示显示五个估计参数及其对应的标准误差（AR（1）条件均值模型具有两个参数，并且GARCH（1,1）条件方差模型具有三个参数）。
推断条件差异和残差
推断并绘制条件方差和标准化残差。 输出对数似然目标函数值。
[res,v,logL] = infer(EstMdl,r);
figure
subplot(2,1,1)
plot(v)
xlim([0,T])
title('Conditional Variance')
subplot(2,1,2)
plot(res./sqrt(v))
xlim([0,T])
title('Standardized Residuals')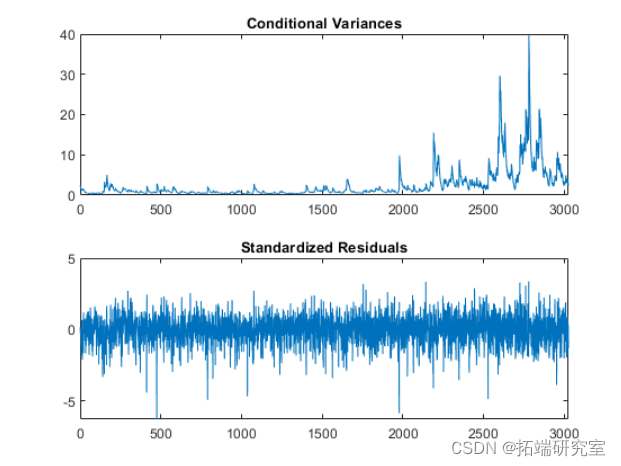
在观察2000之后，条件方差增加。这对应于 看到的增加的波动性。
标准化残差在标准正态分布下具有比预期更大的值 。
适应具有创新分布的模型
修改模型，使其具有Student’s t-innovation分布 ，指定方差模型常量项的初始值。
MdlT = Mdl;
MdlT.Distribution = 't';
EstMdlT = estimate(MdlT,r,'Variance0',{'Constant0',0.001});
ARIMA(1,0,0) Model (t Distribution):
Value StandardError TStatistic PValue
________ _____________ __________ __________
Constant 0.093488 0.016694 5.6002 2.1412e-08
AR{1} 0.13911 0.018857 7.3771 1.6175e-13
DoF 7.4775 0.88261 8.472 2.4125e-17
GARCH(1,1) Conditional Variance Model (t Distribution):
Value StandardError TStatistic PValue
________ _____________ __________ __________
Constant 0.011246 0.0036305 3.0976 0.0019511
GARCH{1} 0.90766 0.010516 86.316 0
ARCH{1} 0.089897 0.010835 8.2966 1.0712e-16
DoF 7.4775 0.88261 8.472 2.4125e-17当t分布 时，系数估计值会略有变化。第二个模型拟合（EstMdlT）有一个额外的参数估计，即t分布自由度。估计的自由度相对较小（约为8），表明明显偏离正常。
随时关注您喜欢的主题
比较模型拟合
使用赤池信息准则（AIC）和贝叶斯信息准则（BIC）比较两种模型拟合 。首先，获得第二拟合的对数似然目标函数值。
[resT,vT,logLT] = infer(EstMdlT,r);
[aic,bic] = aicbic([logL,logLT],[5,6],T) aic = 1×2 103 × 9.4929 9.3807 bic = 1×2 103 × 9.5230 9.4168第二个模型有六个参数，而第一个模型中有五个参数 。尽管如此，两个信息标准都支持具有学生t分布的模型。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
MATLAB深度学习Transformer神经网络量化金融时间序列预测交易策略回测
MATLAB用CNN-LSTM神经网络的语音情感分类深度学习研究
Python注意力机制Attention下CNN-LSTM-ARIMA混合模型预测中国银行股票价格|附数据代码
Python用CNN – LSTM、ARIMA、Prophet股票价格预测的研究与分析|附数据代码
