如果你正在进行统计分析：想要加一些先验信息，最终你想要的是预测。
所以你决定使用贝叶斯。
但是，你没有共轭先验。
Hamiltonian采样器在利用梯度、仿造哈密顿力学系统构造canonical distribution的同时，放弃了MCMC的Markov Chain，( Note: 也有利用梯度的MCMC，比如Metropolis-adjusted Langevin algorithm (MALA)）。但HMC的问题是，需要手动设定每次采样需要的迭代次数（iteration number for leapfrog algorithm），所以有时间步长、迭代次数、速度的分布、初始点的分布这几个要设定。而NUTS首先向解决的是动态设置迭代次数的问题。
依旧是对待采样分布构造一个canonical distribution和哈密顿系统，初始化除了时间步长L外的变量。不一样的地方是，在确定了初始速度 之后，再来个大小相等的反向速度
，然后投硬币确定是走正向还是反向，每次走的总的
，经历step迭代次数的leapfrog之后，j+=1，重新投硬币，如此循环，直到不满足No-U-turn的条件，获取当前轨迹里的随机某个样本。而No-U-Turn的条件是，
或者
，这里
和
分别是positive初始速度那一侧目前到达的位置、速度，
和
同理。也就是说，如果positive和negative两个轨迹中任何一个想要缩小两者之间距离的时候就停止，非常巧妙地利用了一个简单的条件，去估计当前分布的空间尺度。
你可能会花费很长时间编写 Metropolis-Hastings 代码，优化接受率和提议分布，或者你可以使用 RStan。
Hamiltonian Monte Carlo（HMC）
HMC 是一种为 MH 算法生成提议分布的方法，该提议分布被接受的概率很高。具体算法过程请查看参考文献。
打个比方：
给粒子一些动量。
它在滑冰场周围滑行，大部分时间都在密度高的地方。
拍摄这条轨迹的快照为后验分布提供了一个建议样本。
然后我们使用 Metropolis-Hastings 进行校正。
NUTS采样器（No-U-turn Sampler）
HMC，像RWMH一样，需要对步骤的数量和大小进行一些调整。
No-U-Turn Sampler “或NUTs（Hoffman和Gelman（2014）），对这些进行了自适应的优化。
NUTS建立了一组可能的候选点，并在轨迹开始自相矛盾时立即停止。
Stan 的优点
可以产生高维度的提议，这些提议被接受的概率很高，而不需要花时间进行调整。
有内置的诊断程序来分析MCMC的输出。
在C++中构建，所以运行迅速，输出到R。
示例
如何使用 LASSO 构建贝叶斯线性回归模型。
构建 Stan 模型
数据：n、p、Y、X 先验参数，超参数
参数：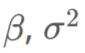
模型：高斯似然、拉普拉斯和伽玛先验。
输出：后验样本，后验预测样本。
数据
int<lwer=0> n; vectr\[n\] y; rel<loer=0> a;
参数
vetor\[p+1\] beta; real<lowr=0> siga;
转换后的参数（可选）
vectr\[n\] liped; lnpred = X*bea;
模型
bta ~ dolexneial(0,w); siga ~ gama(a,b);
或没有矢量化，
for(i in 1:n){
y\[i\]~noral(X\[i,\]*beta,siga);
}
生成的数量（可选）
vecor\[n\] yprict;
for(i in 1:n){
prdit\[i\] = nrmlrng(lnprd\[i\],siga);
对后验样本的每一个元素都要评估一次这个代码。
职业声望数据集
这里我们使用职业声望数据集，它有以下变量
教育：职业在职者的平均教育程度，年。
收入：在职者的平均收入，元。
女性：在职者中女性的百分比。
威望：Pineo-Porter的职业声望得分，来自一项社会调查。
普查：人口普查的职业代码。
类型：职业的类型
bc: 蓝领
prof: 专业、管理和技术
wc: 白领
在R中运行
library(rstan) stan(file="byLASO",iter=50000)
随时关注您喜欢的主题
在3.5秒内运行25000次预热和25000次采样。
第一次编译c++代码，所以可能需要更长的时间。
绘制后验分布图
par(mrow=c(1,2)) plot(denty(prs$bea)
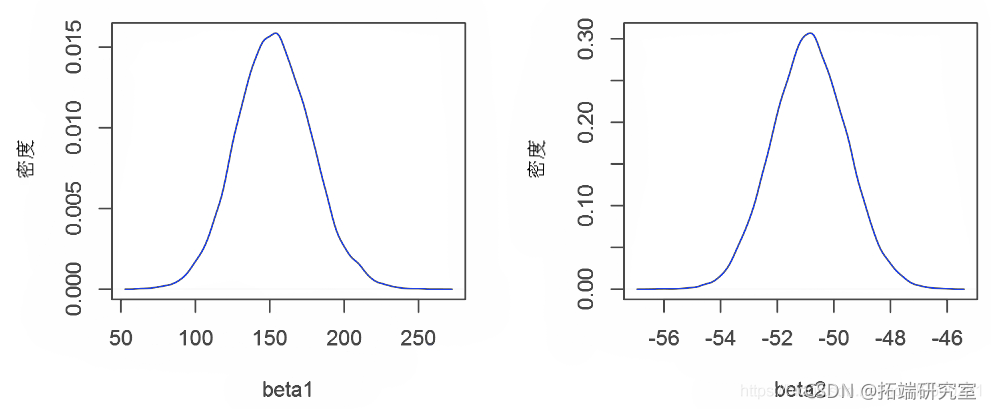
预测分布
plot(density)
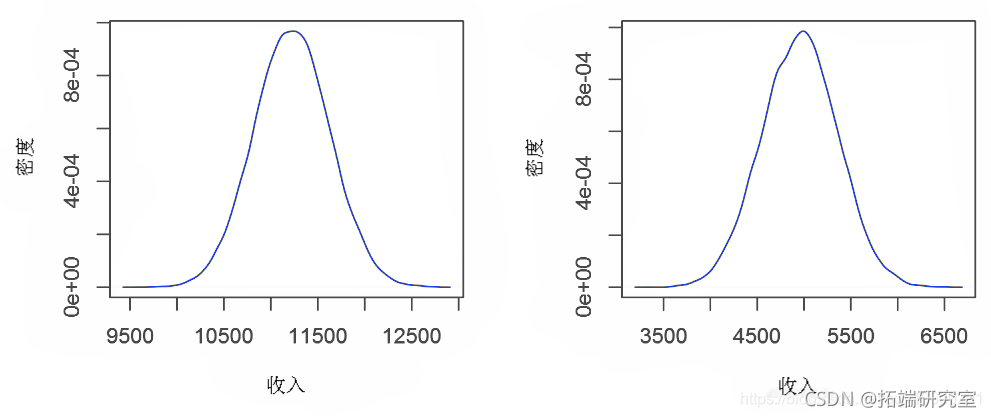
链诊断
splas\[\[1\]\[1:5,\]
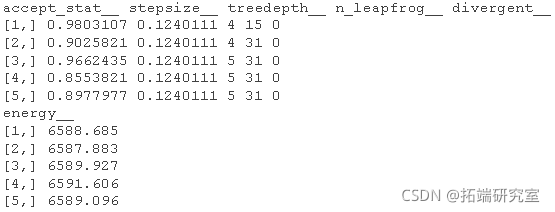
链诊断
trac("beta" )
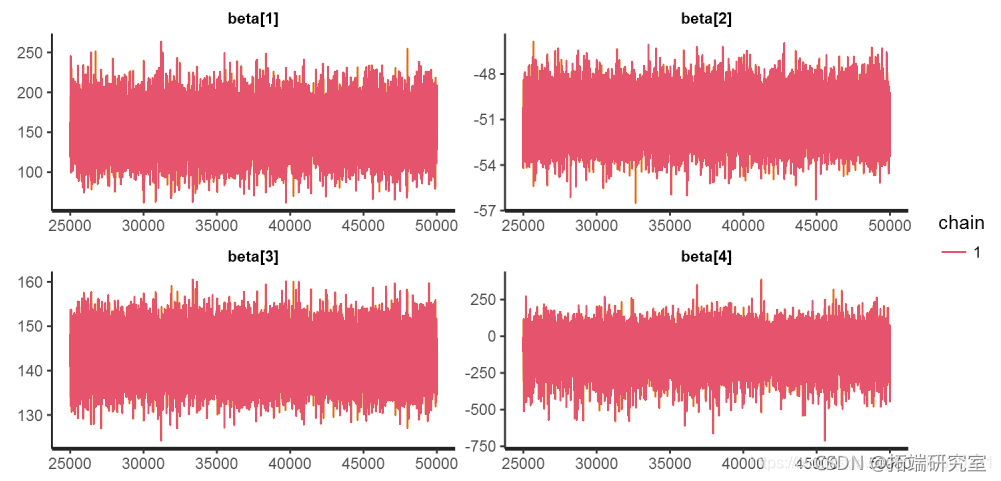
链诊断
pa(pars="beta")
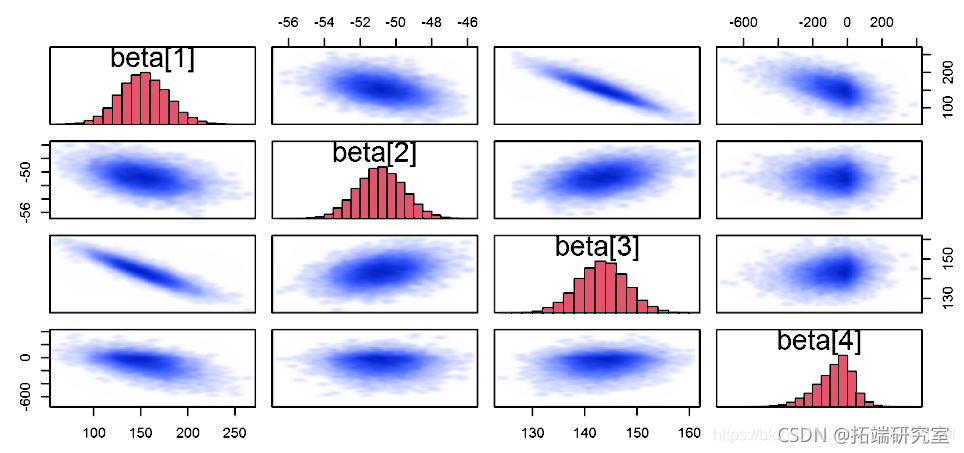
更多链诊断
Stan 还可以从链中提取各种其他诊断，如置信区间、有效样本量和马尔可夫链平方误差。
链的值与各种链属性、对数似然、接受率和步长之间的比较图。
Stan 出错
stan使用的步骤太大。
可以通过手动增加期望的平均接受度来解决。
adapt_delta，高于其默认的0.8
stan(cntl = list(datta = 0.99, mxrh = 15))
这会减慢你的链的速度，但可能会产生更好的样本。
自制函数
Stan 也兼容自制函数。
如果你的先验或似然函数不标准，则很有用。
model {
beta ~ doubexp(0,w);
for(i in 1:n){
logprb(‐0.5*fs(1‐(exp(normalog(
siga))/yde));
}
}
结论
不要浪费时间编码和调整 RWMH.
Stan 运行得更快，会自动调整，并且应该会产生较好的样本。
参考文献
Alder, Berni J, and T E Wainwright. 1959. “Studies in Molecular Dynamics. I. General Method.” The Journal of Chemical Physics 31 (2). AIP: 459–66.
Hoffman, Matthew D, and Andrew Gelman. 2014. “The No-U-Turn Sampler: Adaptively Setting Path Lengths in Hamiltonian Monte Carlo.” Journal of Machine Learning Research 15 (1): 1593–1623.
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
MATLAB贝叶斯优化混合Bayes-CNN-RNN分析股票市场数据与浅层网络超参数优化
R语言贝叶斯分析：INLA 、MCMC混合模型、生存分析肿瘤临床试验、间歇泉喷发时间数据应用|附数据代码
【专题】2024网络主播新职业发展报告汇总PDF洞察（附原数据表）
R语言基于贝叶斯分层、层次Hierarchical Bayesian模型的房价数据空间分析
