
用于R语言的多层感知器(MLP)和极限学习机(ELM)进行时间序列预测。
请注意,由于神经网络无法利用GPU处理,因此大型网络的训练速度往往很慢。
与现有神经网络实现的不同之处在于,R可以自动设计具有合理预测性能的网络。这增加了神经网络的鲁棒性,但也有助于减少训练时间。
可下载资源
使用MLP进行预测
使用R软件包,您可以生成外推(单变量)预测,也可以包含解释变量。
单变量预测
最简单的形式,您只需输入要建模的时间序列。
极限学习机(extreme learning machine)ELM是一种简单易用、有效的单隐层前馈神经网络SLFNs学习算法。2004年由南洋理工大学黄广斌副教授提出。传统的神经网络学习算法(如BP算法)需要人为设置大量的网络训练参数,并且很容易产生局部最优解。极限学习机只需要设置网络的隐层节点个数,在算法执行过程中不需要调整网络的输入权值以及隐元的偏置,并且产生唯一的最优解,因此具有学习速度快且泛化性能好的优点。
其主要思想是:输入层与隐藏层之间的权值参数,以及隐藏层上的偏置向量参数是 once for all 的(不需要像其他基于梯度的学习算法一样通过迭代反复调整刷新),求解很直接,只需求解一个最小范数最小二乘问题(最终化归成求解一个矩阵的 Moore Penrose广义逆问题)。因此,该算法具有训练参数少、速度非常快等优点。接下来的若干年,黄教授带领的团队在此基础上又做了更多的发展,例如,将ELM推广到复数域,提出基于 ELM 的在线时序算法等等。
fit1 <- MLPfit(Air) print(fit1)

输出表明结果网络具有5个隐藏节点,对其进行了20次训练,并使用中位数运算组合了不同的预测。自动生成网络集合,其训练从不同的随机初始权重开始。此外,它提供了网络中包含的输入。
可以使用plot() 获得直观的摘要 。
plot(fit1)
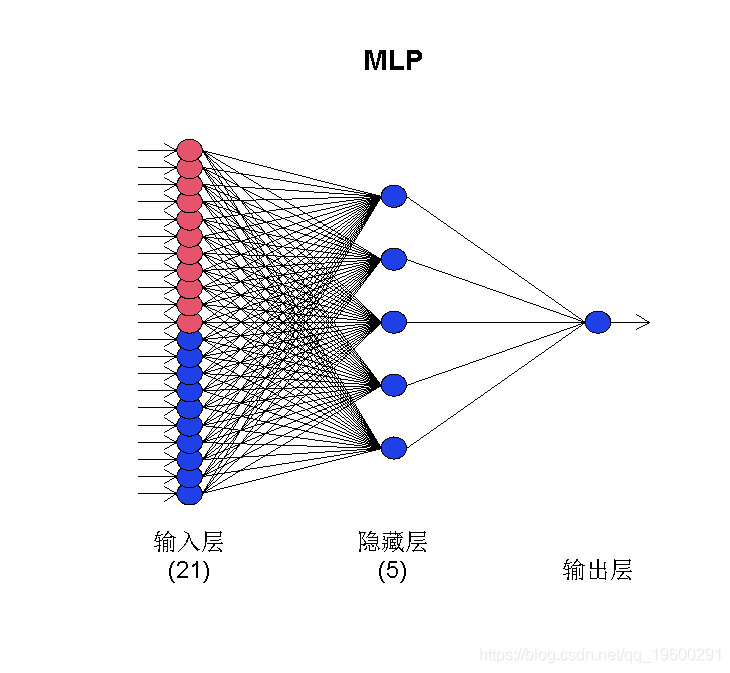
灰色的输入节点是自回归,而洋红色的则是确定性输入(在这种情况下为季节性)。如果包括任何其他回归变量,它们将以浅蓝色显示。
该 MLP() 函数接受几个参数来微调生成的网络。该 hd 参数定义了固定数量的隐藏节点。如果是单个数字,则神经元排列在单个隐藏节点中。如果是矢量,则将它们排列成多层。
fit( hd = c(10,5))

稍后我们将介绍如何自动选择节点数。根据我的经验(以及来自文献的证据),预测单个时间序列的常规神经网络无法从多个隐藏层中获得更好效果。预测问题通常并不那么复杂!
reps 定义了使用多少次训练重复。如果您想训练一个单一的网络,则可以使用 reps=1,有大量结果证据表明这样效果一般。默认值 reps=20 是训练速度和性能之间的折衷,但是您可以承受的重复次数越多越好。当重新训练网络时,它们不仅有助于模型的性能,而且还有助于结果的稳定性。
lags 允许您选择网络考虑的自回归滞后。如果未提供此参数,则网络使用lag 1到lag m,即序列的季节。
lags=1:24

keep=c(rep(TRUE,12), rep(FALSE,12)))

lags=1:24, sel.lag=FALSE

在第一种情况下,滞后(1,2,4,7,8,9,10,11,12,13,18,21,23,24)被保留。在第二种情况下,保留所有1-12,其余13-24被测试是否保留。
神经网络在建模趋势方面并不出色。因此,在对趋势进行建模之前将其消除是很有用的。这由参数处理 difforder。如果 difforder=0 不执行任何差分。对于 diff=1,执行一阶差分。同样,如果 difforder=12 执行12阶差分。如果时间序列是具有季节性周期12的季节性序列,则这是季节性差异。
您可以同时执行 difforder=c(1,12) 或执行任何其他差分。如果 difforder=NULL 然后代码自动决定。如果存在趋势,则使用一阶差分。该序列还经过季节性测试。如果存在,则使用Canova-Hansen检验来确定这是确定性的还是随机的。如果是后者,则还会添加季节性差分。
确定性季节性可以使用季节性虚拟变量更好地建模。
隐藏的节点数可以使用参数预设。默认情况下,这使用验证样本(时间序列的20%)进行测试,或 type="cv" 使用5倍交叉验证。
auto.type="valid",hd.max=8

随时关注您喜欢的主题
鉴于训练神经网络非常耗时,因此你可以重用已经指定/经过训练的网络。在以下示例中,我们将重用 fit1 到新的时间序列。
fit(x, model=fit1)

保留了的模型参数 fit1。如果您只想使用参数,但要对网络进行训练,则可以使用参数 retrain=TRUE。

观察两个设置之间的样本内MSE的差异。
最后,您可以使用省略号将参数直接传递给用于训练网络的 函数 ...
要生成预测,我们使用函数forecast(),该函数 需要训练的网络对象和预测范围 h。
print(frc)

plot(frc)
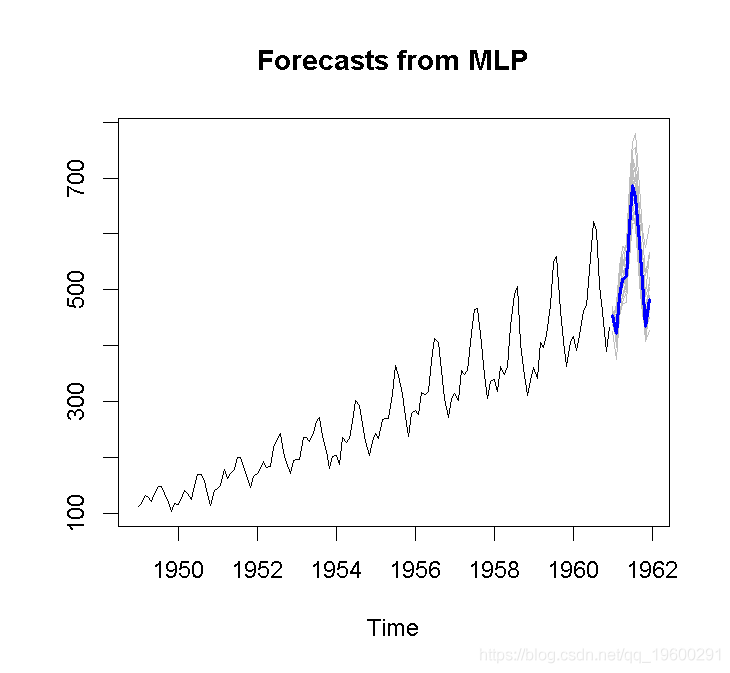
预测图以灰色提供了所有集合的预测。
让我们假设我们要使用确定性趋势来预测时间序列。首先,我们构造输入,然后对序列建模。
使用回归预测
z <- 1:(length()+24) # 我为预测增加了24个额外的观测值 z <- cbind(z) # 把它转换成一个列数 # 添加一个滞后0的回归因子,并强制它留在模型中 difforder=0) # 不要让mlp()来删除随机趋势

输出反映了包含回归变量。这在带有浅蓝色输入的网络图中反映出来。
plot(fit4)
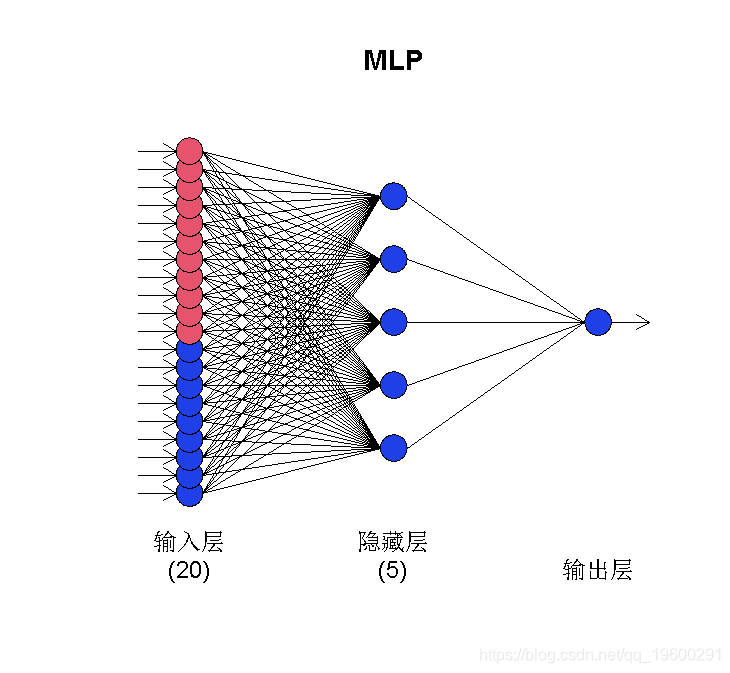
为了包括更多的滞后,我们扩展了 xreg.lags:
difforder=0,xreg=z,xreg.lags=list(1:12)

观察到网络中未包含任何变量。我们使用 xreg.keep 来强制包含这些变量。
difforder=0,xreg=z,xreg.lags=list(1:12),xreg.keep=list(c(rep(TRUE,3),rep(FALSE,9)

显然,神经网络不喜欢确定性趋势!如果我们强制执行,它只会保留它。为此,我将尝试tsutils 包。
zz <- cbind(z, 0) zz\[loc,2\] <- 1 fitxreg.lags=list(c(0:6),0),xreg.keep=list(rep(FALSE,7),TRUE)

显然,您可以包含任意数量的回归变量。
为了产生预测,我们使用 forecast() 函数,但现在使用 xreg 输入。方法是从网络训练期间使用的相同观察值开始输入回归变量,并根据需要扩展预测范围。您
frc.reg <- forecast(fit5,xreg=zz)
ELM的预测
使用极限学习机(EML)。默认情况下,ELM从一个非常大的隐藏层(100个节点)开始,并根据需要对其进行修剪。
print(fit6)

plot(fit6)
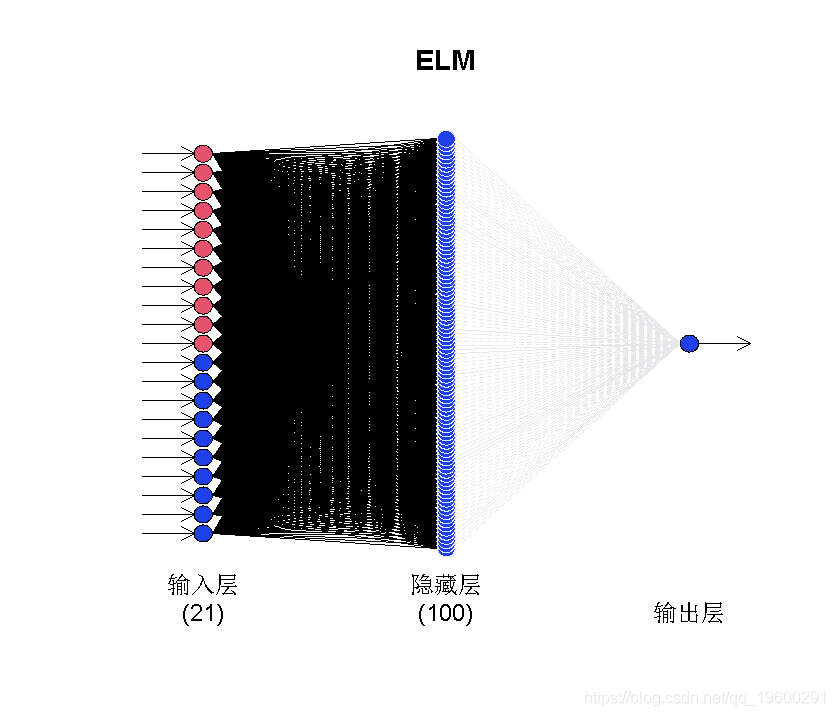
网络图有一些黑线和一些灰线。后者被修剪。装有20个网络(由参数控制 reps)。每个网络可能具有不同的最终连接。
par(mfrow=c(2,2))
for (i in 1:4){plot(fit6,i)}
par(mfrow=c(1,1))
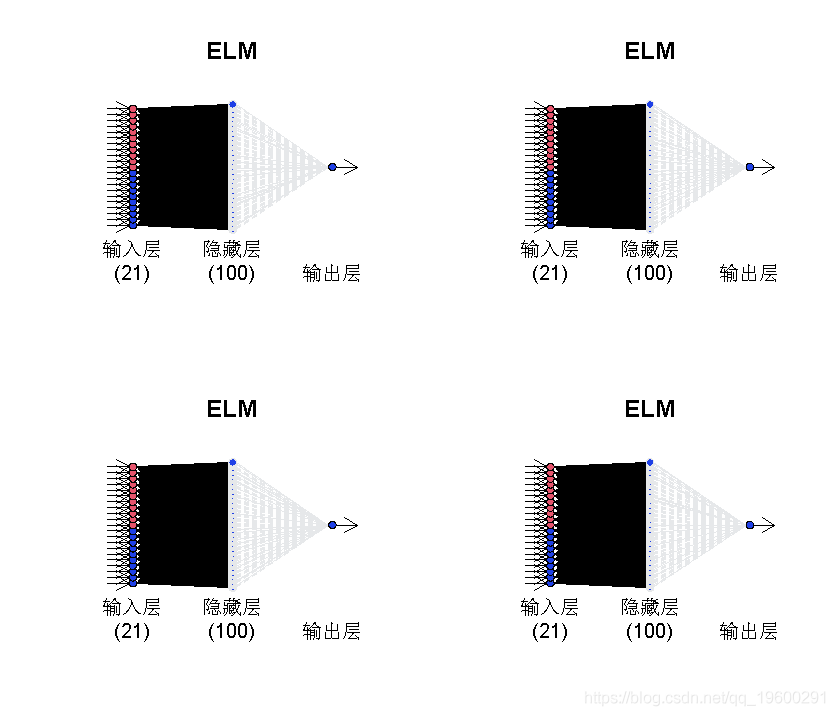
修剪的方式由参数控制。默认选项是使用LASSO回归(类型=“套索LASSO”)。或者,可以使用“ ridge”进行岭回归,使用“ step”进行逐步OLS,使用“ lm”获得OLS解决方案而不进行修剪。
要进行预测,使用forecast() 。
forecast(fit6,h=12)
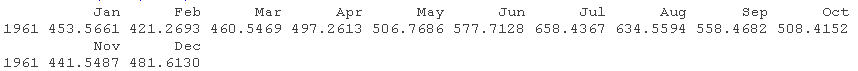
时间层次结构
实现时间层次结构mlp和`elm。`
par(mfrow=c(1,2)) plot(thiMLP) plot(thiELM) par(mfrow=c(1,1))
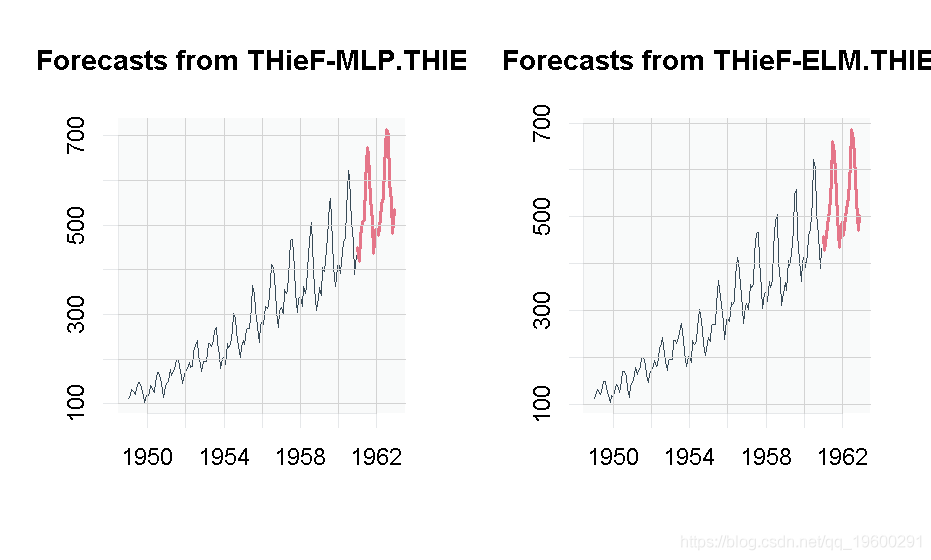
这应该使您可以进行神经网络的时间序列预测。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!



 SPSS与Python用Resblock优化BP神经网络分析慢性胃炎病历数据聚类K-means/AGNES、关联规则挖掘及预测
SPSS与Python用Resblock优化BP神经网络分析慢性胃炎病历数据聚类K-means/AGNES、关联规则挖掘及预测 Python神经网络、随机森林、PCA、SVM、KNN及回归实现ERα拮抗剂、ADMET数据预测|附代码数据
Python神经网络、随机森林、PCA、SVM、KNN及回归实现ERα拮抗剂、ADMET数据预测|附代码数据 Python农作物种植策略研究GA-BP神经网络、蒙特卡洛算法、自注意力Stacking集成模型及粒子群算法PSO优化基于华北山区乡村农作物数据及地块数据
Python农作物种植策略研究GA-BP神经网络、蒙特卡洛算法、自注意力Stacking集成模型及粒子群算法PSO优化基于华北山区乡村农作物数据及地块数据 MATLAB奥运会奖牌预测研究 —CNN神经网络、逻辑回归、Liang-Kleeman信息流、多元回归及随机森林模型的因果关联与概率预测|附代码数据
MATLAB奥运会奖牌预测研究 —CNN神经网络、逻辑回归、Liang-Kleeman信息流、多元回归及随机森林模型的因果关联与概率预测|附代码数据



