本文提供了一套用于分析各种有限混合模型的方法。
既包括传统的方法,如单变量和多变量正态混合的EM算法,也包括反映有限混合模型的一些最新研究的方法。许多算法都是EM算法或基于类似EM的思想,因此本文包括有限混合模型的EM算法的概述。
1.有限混合模型介绍
人群中的个体往往可以被划分为群。然而,即使我们观察到这些个体的特征,我们也可能没有真正观察到这些成员的群体。
有限混合模型的数据生成过程可以看做是,先从k个模型中选择一个,然后利用这个模型的概率分布生成数据。从k个模型中选择一个模型部分的参数为一个向量,这个向量的每一个元素对应每个模型的选中概率,和为1。
如果我们写出这个参数的似然函数,其实就是一个多项式分布,基于贝叶斯学派的观点,需要为参数赋予一个先验分布,就是赋予其主观上的概率分布特点,再乘上似然函数,其实就是使用观测数据修正一开始的概率分布认识,从而得到后验分布。
那么加什么先验呢?最简单的就是均匀分布的多变量版本,然后算出后验分布后发现,是狄利克雷分布,而均匀分布的多变量版本其实就是对称的狄利克雷分布,也就是狄利克雷分布的特例。先验和后验是同家族的函数,所以多项式分布和狄利克雷分布是共轭的。共轭的好处就是每次迭代只需简单地根据已有的公式更新参数就好了。
总结:狄利克雷分布常被选做是有限混合模型中的一个参数的先验分布,因为该参数的似然函数和狄利克雷分布是共轭的。
至于狄利克雷过程,是狄利克雷分布的无限版本。它一般作为无限混合模型的参数的先验。
这项任务在文献中有时被称为 “无监督聚类”,事实上,混合模型一般可以被认为是由被称为 “基于模型的聚类 “的聚类方法的子集组成。
有限混合模型也可用于那些对个体聚类感兴趣的情况之外。首先,有限混合模型给出了整个子群的描述,而不是将个体分配到这些子群中。有时,有限混合模型只是提供了一种充分描述特定分布的手段,例如线性回归模型中存在异常值的残差分布。
无论建模者在采用混合模型时的目标是什么,这些模型的大部分理论都涉及到一个假设,即子群是按照一个特定的参数形式分布的–而这个形式往往是单变量或多变量正态。
最近的研究目标是放宽或修改多变量正态假设,有限混合模型分析的计算技术,其中的成分是回归、多变量数据离散化产生的向量,甚至是完全未指定的分布。
2. 有限混合模型的EM算法
EM算法迭代最大化,而不是观察到的对数似然Lx(θ),算式为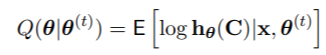
1. E步:计算Q(θ|θ(t))
2. M步骤:设定θ(t+1)=argmaxθ∈Φ Q(θ|θ(t))
对于有限混合模型,E步骤不依赖于F的结构,因为缺失数据部分只与Z有关。
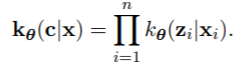
Z是离散的,它们的分布是通过贝叶斯定理给出的。M步骤本身可以分成两部分,与λ有关的最大化,它不依赖于F,与φ有关的最大化,它必须为每个模型专门处理(例如,参数化、半参数化或非参数化)。因此,模型的EM算法有以下共同特点。
11. E步。计算成分包含的 “后验 “概率(以数据和θ(t)为条件)。
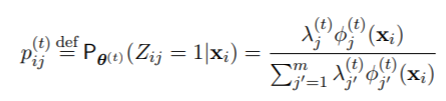
对于所有i = 1, . . . ,n和j = 1, . . . 从数值上看,完全按照公式(2)的写法来实现是很危险的,因为在xi离任何一个成分都很远的情况下,所有的φ(t)j 0(xi)值都会导致数值下溢为零,所以可能会出现不确定的形式0/0。因此,许多例程实际上使用的是等价表达式
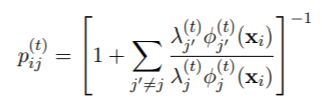
或其某种变体。
2. λ的M步骤。设
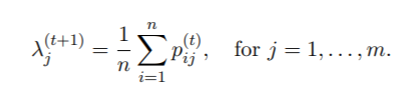
2.3. 一个EM算法的例子
作为一个例子,我们考虑对图1中描述的间歇泉喷发间隔时间等待数据进行单变量正态混合分析。这种完全参数化的情况对应于第1节中描述的单变量高斯家族的混合分布,其中(1)中的第j个分量密度φj(x)为正态,均值为μj,方差为σ 2 j。
对于参数(µj , σ2 j )的M步,j = 1, . . 这个EM算法对这种单变量混合分布的M步骤是很简单的,例如可以在McLachlan和Peel(2000)中找到。
mixEM(waiting, lambda = .5)
上面的代码将拟合一个二成分的混合分布(因为mu是一个长度为2的向量),其中标准偏差被假定为相等(因为sigma是一个标量而不是一个向量)。
随时关注您喜欢的主题
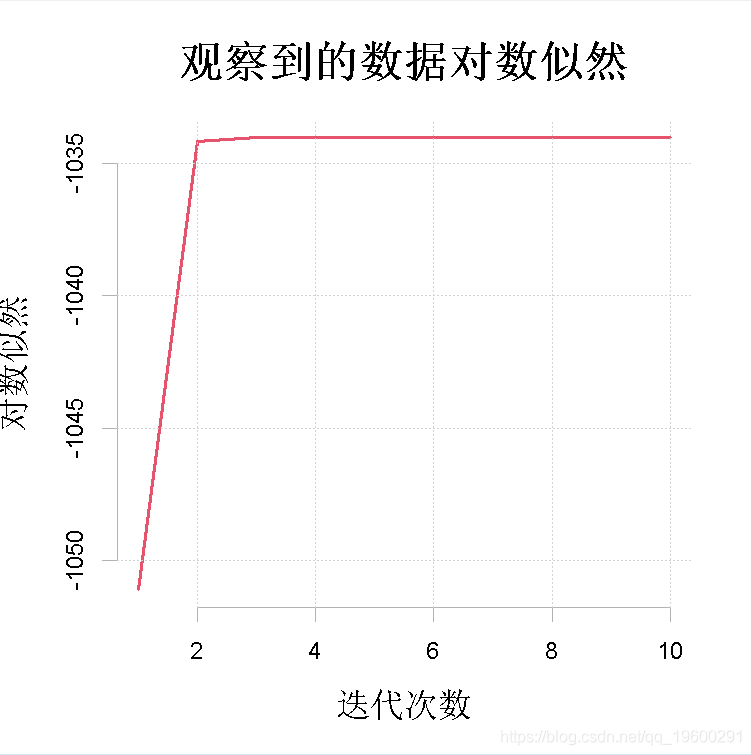
图1:对数似然值的序列,Lx(θ (t))
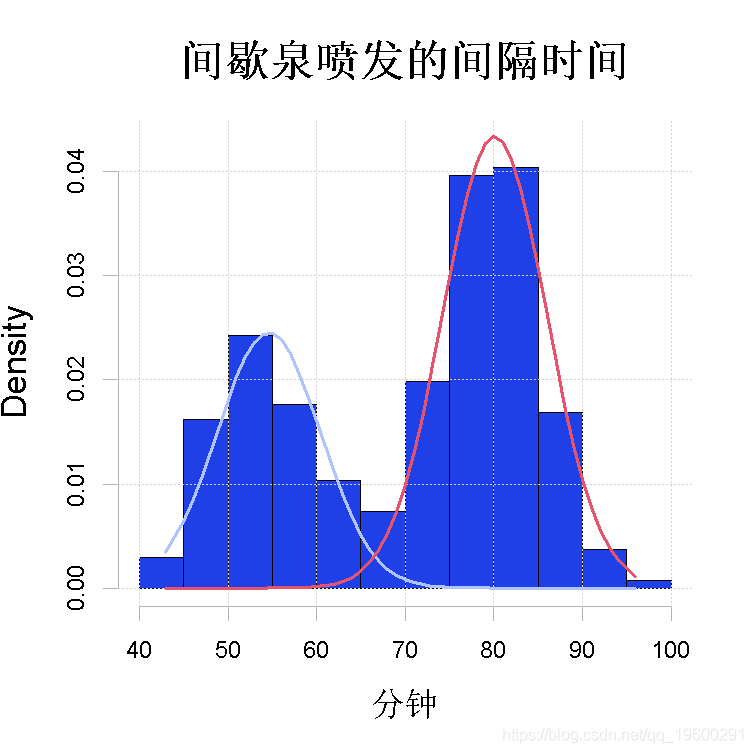
图2:用参数化EM算法拟合间歇泉等待数据。拟合的高斯成分。
R> plot(wait1, density = TRUE, cex.axis = 1.4, cex.lab = 1.4, cex.main = 1.8,
+ main2 = "Time between Old Faithful eruptions", xlab2 = "Minutes")两个图:观察到的对数似然值的序列t 7→Lx(θ (t))和数据的直方图,其中有N(ˆµj , σˆ 2 j)的m(这里m=2)个拟合的高斯分量密度,j=1, . . . ,m,叠加在一起。估计θˆ
另外,使用summary也可以得到同样的输出。
summary(wait1)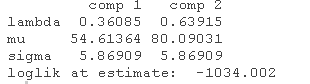
3. Cutpoint methods切割点方法
传统上,大多数关于有限混合模型的文献都假设方程(1)的密度函数φj(x)来自一个已知的参数族。然而,一些作者最近考虑了这样的问题:除了确保模型中参数的可识别性所需的一些条件外,φj(x)是不指定的。我们使用Elmore等人(2004)的切割点方法。
我们参考Elmore等人从-63开始,一直到63大约以10.5的间隔采用切点。然后从原始数据中创建一个多指标数据集,如下所示。
R> cutpts <- 10.5*(-6:6)
R> mult(data, cuts = cutpts)一旦创建了多指标数据,我们可以应用EM算法估计多指标参数。最后,计算并绘制出方程的估计分布函数。
图3给出了3分量和4分量解决方案的图表;这些图表与Elmore等人(2004)的图1和图2中的相应图表非常相似。
R> plot(data, posterior, lwd = 2,
+ main = "三分量解")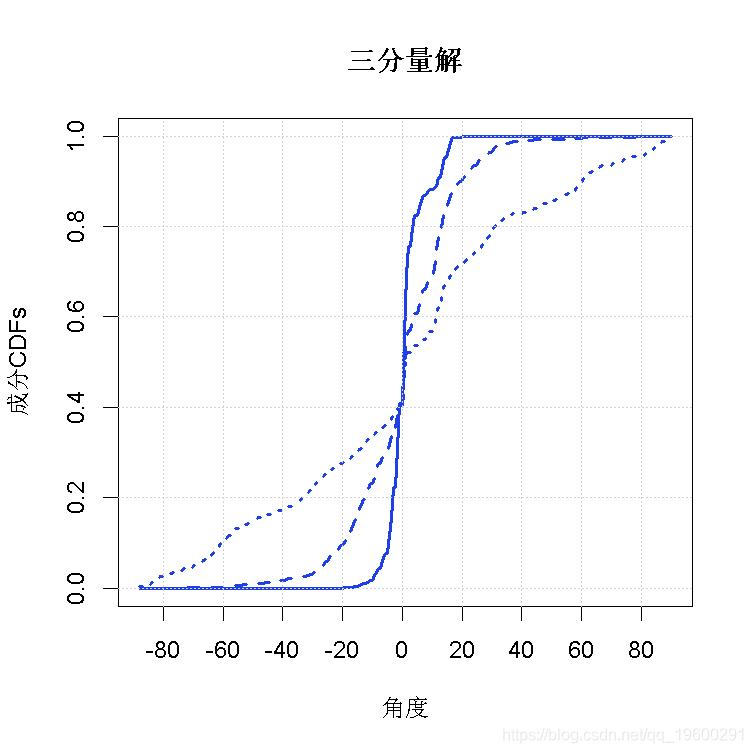 图3(a)
图3(a)
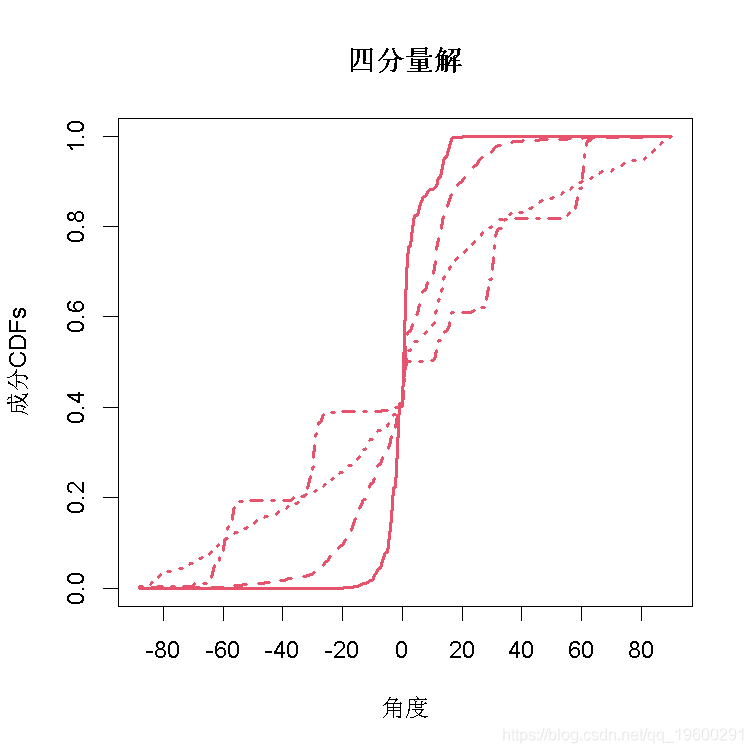 图3(b)
图3(b)
同样可以用summary来总结EM输出。

单变量对称、位置偏移的半参数例子
在φ(-)相对于Lebesgue度量是绝对连续的额外假设下,Bordes等人(2007)提出了一种估计模型参数的随机算法,即(λ, µ, φ)。一个特例
R> plot(wait1, which = 2 )
R> wait2 <-EM(waiting)
R> plot(wait2, lty = 2)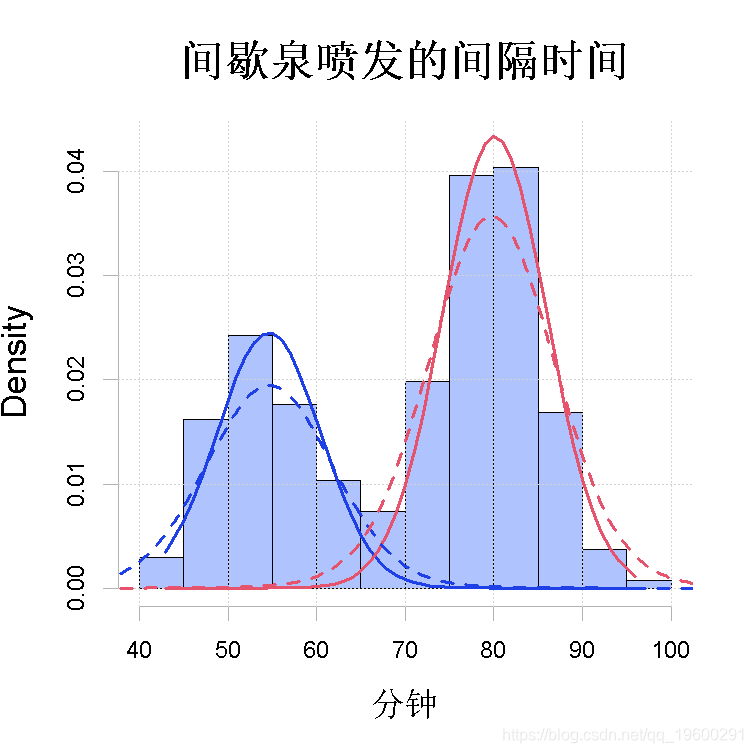 图4(a)
图4(a)
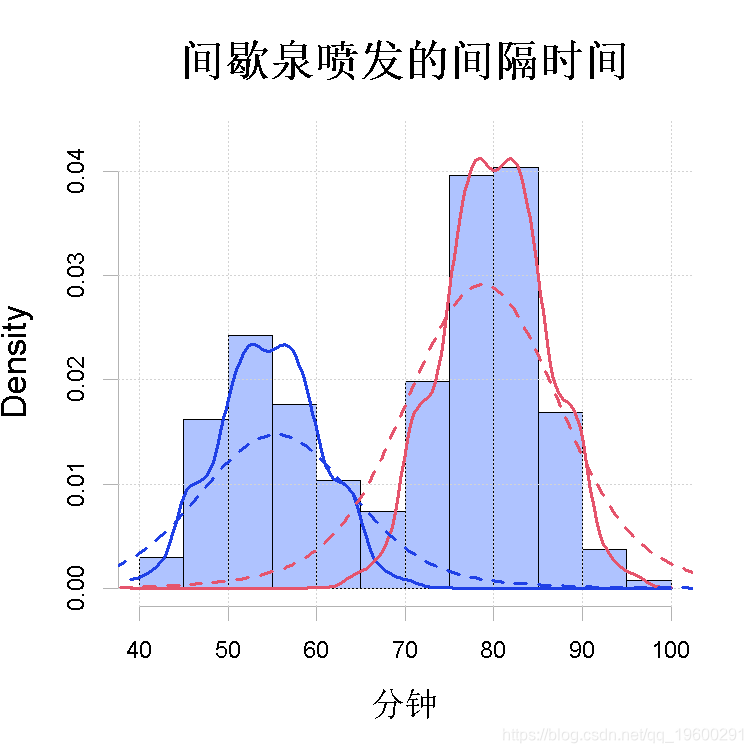
图4(b)
因为半参数版本依赖于核密度估计步骤(8),所以有必要为这个步骤选择一个带宽。默认情况下,使用”Silverman的经验法则”(Silverman 1986)应用于整个数据集。
R> bw.nrd0(wait)
但带宽的选择会产生很大的不同,如图4(b)所示。
> wait2a <- EM(wait, bw = 1)
> plot(wait2a
> plot(wait2b我们发现,在带宽接近2的情况下,半参数解看起来非常接近图2的正态混合分布解。进一步降低带宽会导致图4(b)中的实线所表现出的 “凹凸不平”。另一方面,在带宽为8的情况下,半参数解效果很差,因为算法试图使每个成分看起来与整个混合分布相似。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 投资组合优化实战:Python与蒙特卡洛模拟、SLSQP算法、差分进化多目标规划在资产配置中的应用与非线性交易费用处理创新 | 附代码数据
投资组合优化实战:Python与蒙特卡洛模拟、SLSQP算法、差分进化多目标规划在资产配置中的应用与非线性交易费用处理创新 | 附代码数据 2025有色金属行业前瞻报告:信用、ESG、新材料、全球化布局 | 附500+份报告PDF、数据、可视化模板汇总下载
2025有色金属行业前瞻报告:信用、ESG、新材料、全球化布局 | 附500+份报告PDF、数据、可视化模板汇总下载 LLM增强基本面分析:融合收入报表多指标评分与回测验证的算法交易策略 | 附代码数据
LLM增强基本面分析:融合收入报表多指标评分与回测验证的算法交易策略 | 附代码数据



