本文是极端值推断的内容。我们在广义帕累托分布上使用最大似然方法。
最近我们被客户要求撰写关于极值推断的研究报告。在参数模型的背景下，标准技术是考虑似然的最大值（或对数似然）。
- 极大似然估计
考虑到一些技术性假设，如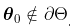 
，
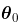的某个邻域，那么
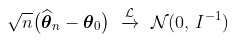
简单说来定义是：
假设们有高维似然函数
那么
叫做对于
的profile likelihood。 这个式子表示你给定任意的
,找到在这个值下面（任意改变
）最大的
：
如果是normal distribution, 对于 和
，
注意和其它的几种似然函数微妙的区别。
estimated likelihood (有时人叫它pseudo likelihood。。随便吧）：先计算你的 再带入似然函数。例如，你可以把normal distribution, sample variance代入，然后得到对于mean的estimated likelihood。注意，对比第一个式子，这里我们需要用
替换
中的
或者
还有一个叫做integrated likelihood：我们假设 是一个目标函数，同时假设我们的参数有概率分布的，那么就可以积分得到marginal distribution
这个个是Bayesian 分析中用的，因为prior就是你的参数分布，必须有这个才能积分。
modified profile likelihood：有些人认为 marginal likelihood才是精确的，但是由于难算，就想用profile likelihood的表达式去近似，最后加上高阶修正；或者利用Laplace approximation理解也可以。要达到的目的就是你的modified profile会更加像marginal likelihood,或者真实likelihood. 个人认为，这就是频率派的人在朝着Bayesian派在Likelihood方法靠拢的做法。
其中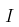
表示费雪信息矩阵。在此考虑一些样本，来自广义帕累托分布，参数为
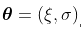，因此
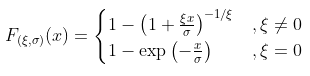
如果我们解决极大似然的一阶条件，我们得到一个满足以下条件的估计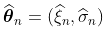
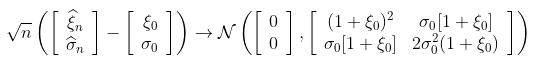
这种渐进正态性的概念如下：如果样本的真实分布是一个具有参数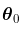
的GPD，那么，如果n足够大，就会有一个联合正态分布
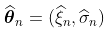。因此，如果我们产生大量的样本（足够大，例如200个观测值），那么估计的散点图应该与高斯分布的散点图相同。
> for(s in 1:1000){
+ param\[s,\]=gpd(x,0)$par.ests
> image(x,y,z)得到一个3D的表示
> persp(x,y,t(z)
+ xlab="xi",ylab="sigma")
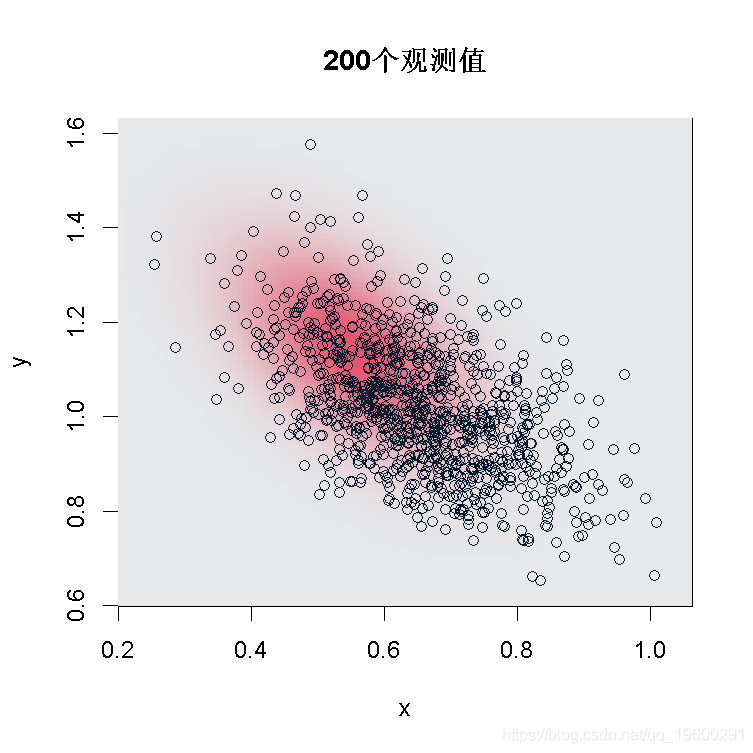
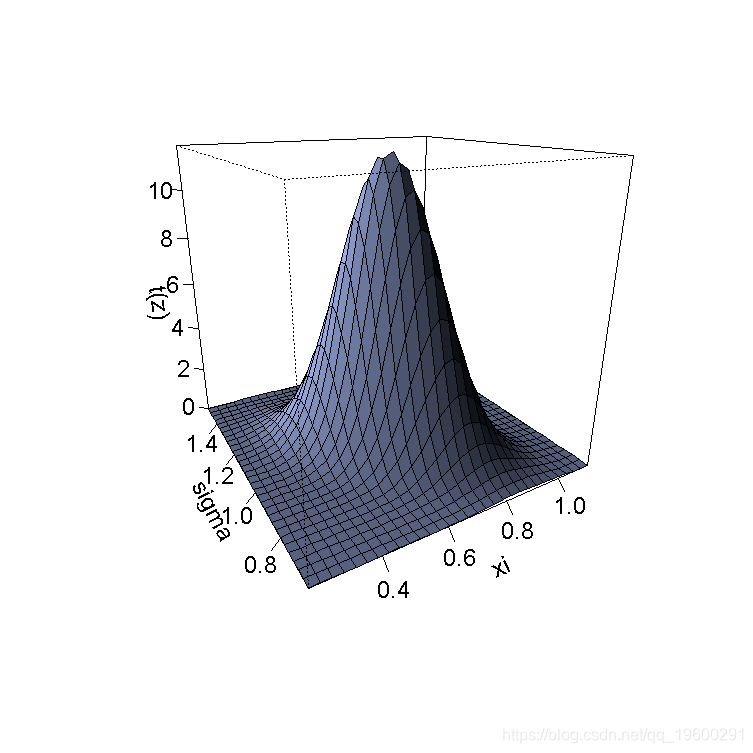
有了200个观测值，如果真正的基础分布是GPD，那么，联合分布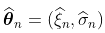
是正态的。
- Delta德尔塔法
另一个重要的属性是德尔塔法。这个想法是，如果是渐进正态，足够平滑，那么也是渐进高斯的。
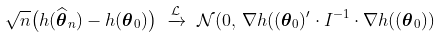
从这个属性中，我们可以得到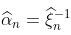
（这是极值模型中使用的另一个参数化）的正态性，或者在任何四分位数
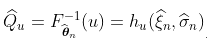上 。我们运行一些模拟，再一次检查联合正态性。
> for(s in 1:1000)
+ gpd(x,0)$par.ests
+ q=sha * (.01^(-xih) - 1)/xih
+ tvar=q+(sha + xih * q)/(1 - xih)
dmnorm(cbind(vx,vy),m,S)
> image(x,y,t(z)随时关注您喜欢的主题
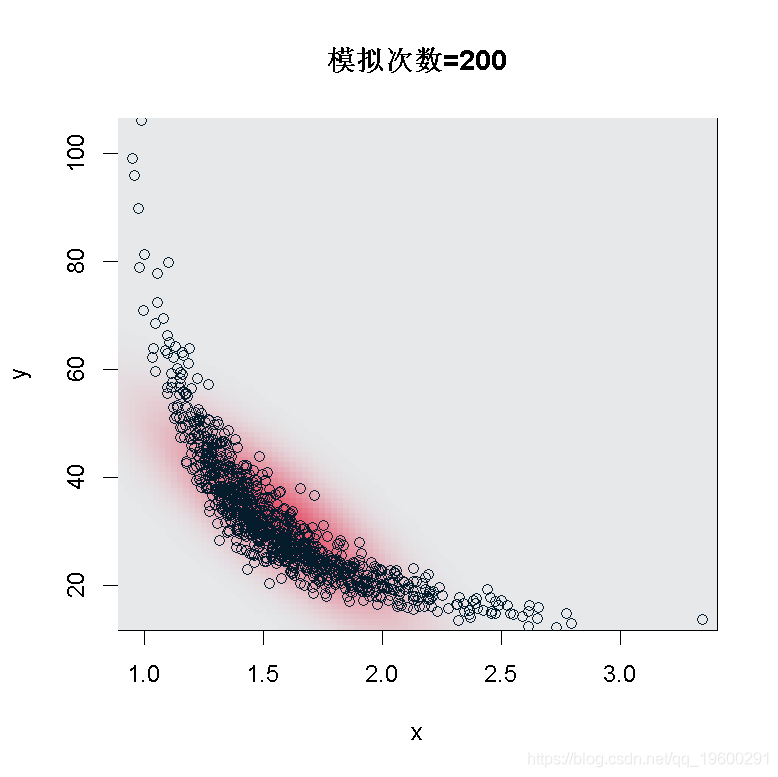
正如我们所看到的，在样本大小为200的情况下，我们不能使用这个渐进式的结果：看起来我们没有足够的数据。但是，如果我们在n=5000运行同样的代码，
``````
> n=5000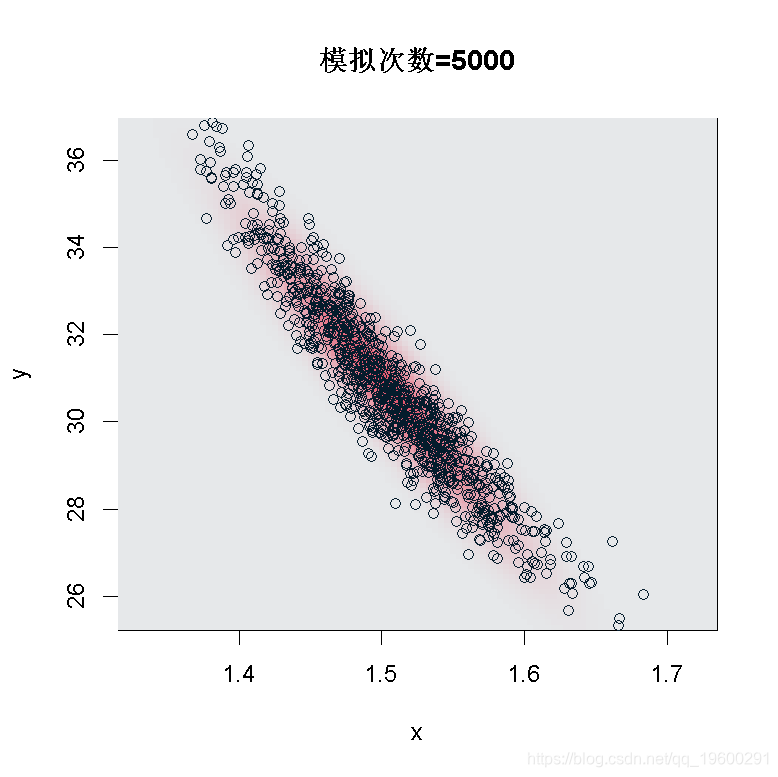
我们得到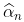
和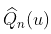
的联合正态性。这就是我们可以从这个结果中得到的delta-方法。
- 轮廓似然( Profile Likelihood )
另一个有趣的方法是Profile 似然函数的概念。因为尾部指数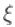
，
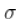在这里是辅助参数。
这可以用来推导出置信区间。在GPD的情况下，对于每个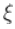
，我们必须找到一个最优的 。我们计算Profile 似然函数，即
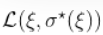。而我们可以计算出这个轮廓似然的最大值。
一般来说，这个两阶段的优化与（全局）最大似然是不等价的，计算结果如下
+ profilelikelihood=function(beta){
+ -loglik(XI,beta) }
+ L\[i\]=-optim(par=1,fn=profilelik)$value }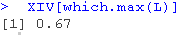
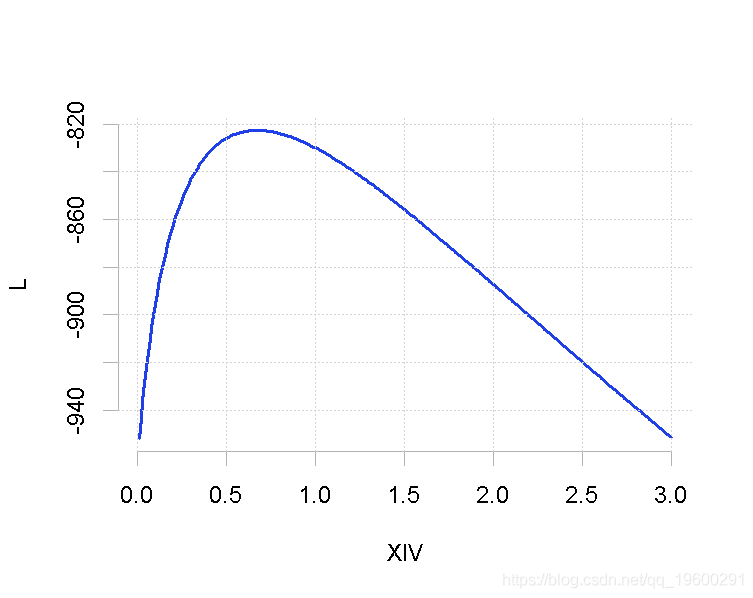
如果我们想计算轮廓似然的最大值（而不是像以前那样只计算网格上的轮廓似然的值），我们使用
+ profile=function(beta){
+ -loglikelihood(XI,beta) }
(OPT=optimize(f=PL,interval=c(0,3)))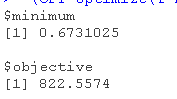
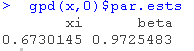
我们得到结果和最大似然估计的
相似。我们可以用这种方法来计算置信区间，在图表上将其可视化
> line(h=-up-qchisq(p=.95,df=1)
> I=which(L>=-up-qchisq(p=.95,df=1))
> lines(XIV\[I\]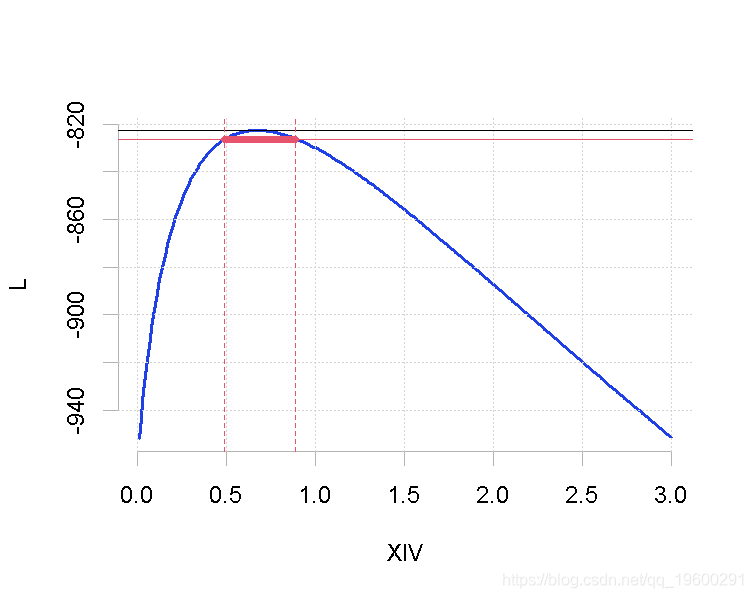
竖线是参数
95%置信区间的下限和上限。
R语言极值分析：分块极大值Block-maxima、阈值超额法threshold excess、广义帕累托分布GPD拟合降雨数据时间序列
R语言用极大似然和梯度下降算法估计GARCH(p)过程
R语言极值理论EVT：基于GPD模型的火灾损失分布分析
使用R语言做极大似然估计实例
