最近我们被客户要求撰写关于面板平滑转换回归(PSTR)的研究报告。建模过程包括三个阶段：表述，估计和评估。
当采用两种状态时，单转换函数PSTR模型具有两个变量：我们的经验方法的基础包括评估N个国家的资本流动性。相应的模型定义如下：
其中，Iit是第i个国家在时间t时观察到的国内投资与GDP的比率，Sit是国内储蓄与GDP的比率，αi表示单个固定效应。
可下载资源
剩余εit假定为i.i.d.（0，σ2ε）。Corbin（2001）特别使用了该模型，该模型有两个主要缺点。
首先，它假设在小组的N个国家之间资本的国际流动程度相同，即βi=β，∀i=1，…，N。很明显，即使仅考虑经合组织国家，这种假设也是不现实的。如前所述，已经确定了许多明显影响资本流动的因素：国家规模、人口年龄结构、开放程度等。因此，假设βi=β意味着这些因素不影响资本流动。这样的假设显然过于严格。
面板平滑转换模型（Panel smooth transmition model）是Gonzalez等（2005）提出的一种面板门槛模型。该模型较好地解决了Hansen的PTR模型中门限值前后跳跃性变化的问题，在模型中加入了一个连续的转换函数，更符合经济现实。除了平滑变换，该模型还具有有效捕捉不同截面间异质性的优势，适合多截面数据研究（如多国面板、或我国省际面板数据）。
PSTR模型基本公式如下：
其中， 为个体效应，
为解释变量线性部分的回归系数，
为解释变量非线性部分的回归系数，
为解释变量，
为随机误差项。
转换函数 满足logistic函数形式，即：
，其中
其中，
为门限变量（可以为解释变量），
为转换函数的斜率系数（即平滑参数），
越大，转换函数斜率越大，表示不同区制间转换速度越大，
为位置参数，r为转化函数的个数，m为转换函数中位置参数的个数。
（这里有些难懂，后续进行PSTR首先也是要进行r和m的确定。简而言之，r表示转换函数的个数，r个转换函数表示模型有r+1个区制。但在每个转换函数中，位置参数个数可能不止一个。位置参数为1个的logistic函数呈标准的S型分布，但2个位置参数则会出现类似尖U型的曲线。）
国内多数学者运用PSTR模型时，较多出现了r=1,m=1（即一个转换函数，转换函数中位置参数为1）的简单情形。但具体r和m的值是需要进行检验的。下面就到了具体PSTR该如何操作啦：
-
进行线性和剩余非线性检验
主要是综合LM、LMF、LRT三者的值，对数据的线性关系进行判断。首先检验线性关系：H0：r=0；H1：PSTR with at least r=1，若检验出LM、LMF、LRT三者p值均小于0.01（1%显著度水平下拒绝）（一般显著的非线性关系p值都为0.000），则拒绝原假设，则模型至少存在一个转换函数。继续进行剩余非线性检验，直到接受原假设，则可初步判断出转换函数个数r的值。（为什么说初步判断呢？后面你就知道了）
2. 位置参数个数m及最优转换函数个数r*(m)的确定
参照r的代码，可对m的值进行修改，一般m选1或2，即可概括出数据特征。分别设定m=1及m=2，然后通过对比模型AIC、SC、RSS的值，选择AIC、SC、RSS小的值，确定合适的m，以及对应的最优r*(m)，这里的r*(m)是根据上文中LMF值确定的，所以与上文并不会存在明显差异。
3. 下面就以选定的m和r*(m)开始PSTR模型的估计啦
r的模型跑出来主要会出现estimated slope parameter of transition function（斜率系数，即平滑参数的估计值）；estimated location parameters（位置参数的估计值）；estimated slope parameters（回归系数）, 这里的位置参数、回归系数，均为每列对应一个转换函数。此外，还会跑出修正后的标准差、t值等。
关于不同区制间解释变量的回归系数，只要画出转换函数的图像，根据图像判断转换函数G在每一段上的取值，即可大概判断，在门限值的两侧，系数稳定的状态。比如，x<c时，G=0, 则系数为 ；x>c时，G=1，则x趋于无穷时，系数趋于
。而在x取值在门限值c附近时，如果门限值为解释变量，则该解释变量的系数存在一个导数的平滑转换，可自行推导。这里只列举了单门限、单转换函数的简单例子，实际情况还需自己画图分析。
其次，方程（1）表明，在模型的估计期内，储蓄保留系数是常数。这一假设也是不现实的，特别是当我们考虑具有足够长时间维度的宏观面板时：很明显，典型经合组织国家的资本流动性在60年代和90年代并不相同。
自70年代中期以来，主要经合组织国家的资本管制和资本跨境流动障碍已经消除，FH系数随着时间的推移呈下降趋势。 实际上，Obstfeld和Rogoff（2000）在1990-1997年期间的回归中发现，经合组织国家的储蓄保留系数为0.60，而FH在1960-74年期间16个经合组织国家的文章中强调的储蓄保留系数为0.89。因此，没有理由假设参数β（参数βi）是时间不变的。
一般来说，这两个问题不能同时解决。例如，可以通过假设FH参数βi是随机分布的来考虑异质面板模型5。然而，在这样一个随机系数模型中，资本的流动性被假定为时间不变的。此外，在一个简单的随机系数模型（Swamy，1970）中，参数βi被假定为独立于解释变量。换言之，假设FH系数与国内储蓄与GDP之比无关。因此，它们的可变性是其他未指明的结构因素的结果。
解决这两个问题的方法是在线性面板模型中引入阈值效应。在这种情况下，第一种解决方案是使用简单面板阈值回归（PTR）模型（Hansen，1999），正如Ho（2003）所建议的那样。在这种情况下，极端状态之间的转移机制非常简单：在每个日期，如果观察到的某个国家的阈值变量小于某个给定值，称为阈值参数，资本流动性是由一个特定的模型（或机制）来定义的，它不同于阈值变量大于阈值参数时使用的模型。例如，让我们考虑一个具有两个极端状态的PTR模型：解决这两个问题的方法是在线性面板模型中引入阈值效应。
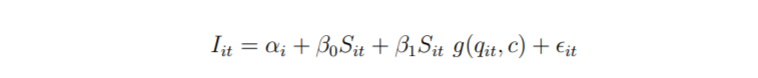
具有单个位置参数（m = 1）的逻辑转换函数：
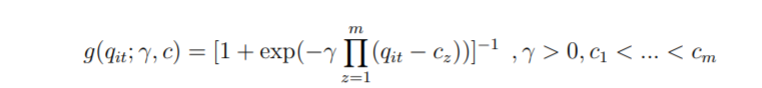
可以证明，I w.r.t S的弹性是时变的
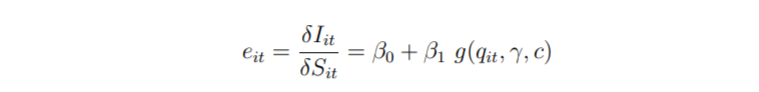
我认为提取这些随时间变化的系数对所有个体来说都是很直观的，因为它们显示了感兴趣的关系的动态，补充了转换函数的可视化。
假设我们将此应用于Hansen数据的情况（4个变量而不是2个变量，但上面的公式适用）。我们想研究债务水平对投资的影响，条件是选择转换变量为托宾Q。让我们首先拟合模型：
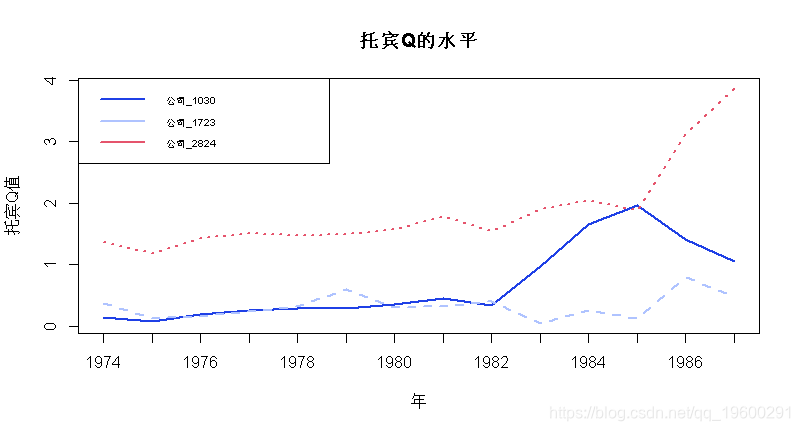
PSTR(data, dep='inva', indep=4:20, indep_k=c('vala','debta','cfa','sales'),tvars=c('vala'), iT=14) 然后计算时变系数，并提取样本中前三家公司的托宾Q水平
for (i in 1:n){
va_i<-vala[cusip==id[i]]
g<-(1+exp(-gamma*(va_i-c)))^(-1)
tvc_i<-est[2] + mbeta*g 最后绘制这些时间序列：
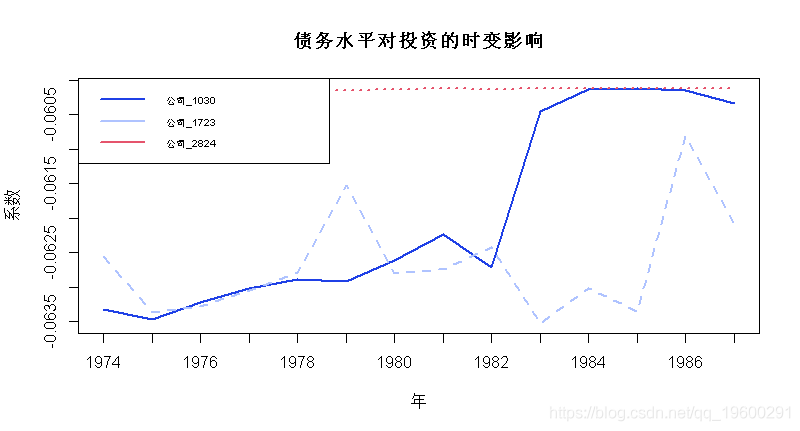
matplot(tvc, type = 'l', lwd=2,col = 1:3, xaxt='n'
axis(1, at=1:nrow(tvc), labels=c(1974:1987)); legend("topleft", legend =
matplot(vala, type = 'l', lwd=2,col = 1:3, xaxt = 'n', xlab='年'
; axis(1, at=1:nrow(tvc), labels=c(1974:1987));
legend("topleft", legend = paste('公司',colnames(vala),sep=''), 我们可以看到，投资w.r.t债务的弹性随着时间的推移而变化，并且取决于Q的水平：Q越高（拥有更多投资机会的公司），影响越强。特别是Q（2824）最高的公司（绿色曲线，右图）表现出最稳定的关系（绿色曲线，左图）。
随时关注您喜欢的主题
有一个问题：如果转换变量与独立变量相同（或它的函数），则弹性的计算变得更加复杂。通常，对于具有R转换函数的模型（R + 1机制），我们有：
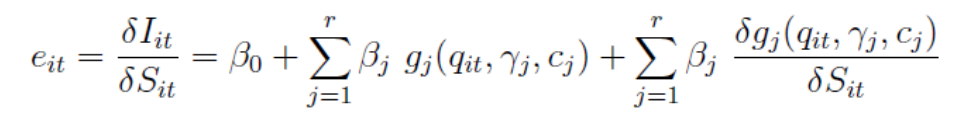
.这意味着投资弹性w.r.t托宾的Q需要用不同的方法来计算。
【专题】2015-2023年中国企业东南亚地区医疗行业投资回顾与展望报告PDF合集分享（附原数据表）
【专题】中国数字科技产业投资发展研究报告PDF合集分享（附原数据表）
【视频】因子分析简介及R语言应用实例：对地区经济研究分析重庆市经济指标
R语言宏观经济学：IS-LM曲线可视化货币市场均衡
