本文将说明金融数学中的R 语言优化投资组合,因子模型的实现和使用。
我们将从一个包含单个已知因子(即市场指数)的简单示例开始。
具有单一市场因素的宏观经济因素模型
我们将从一个包含单个已知因子(即市场指数)的简单示例开始。该模型为
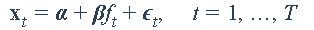
可下载资源
其中显式因子ft为S&P 500指数。我们将做一个简单的最小二乘(LS)回归来估计截距α和加载β:
谈起量化投资之中最为著名的模型,除了CAPM,可能就是Fama和French的三因子模型了。大名鼎鼎的CAPM模型在Markowitz和Sharpe的努力下构建出理论模型后,许多大牛都对其进行过实证检验,包括诺奖得主Scholes、Merton和Fama,这些针对于上世纪70年代以前数据的分析证明CAPM的有效性,但是在70到80年代的研究中,人们却发现股票收益不能被市场贝塔很好地解释,市场异象频生,这意味着,我们还需要用其他的方式来寻找新的因素来分析股票收益的变动。
1992年Fama和French采取横截面回归的方法,研究市场贝塔、账面市值比(下文简称帐市比)、市值、市盈率以及财务杠杆对股票收益率(平均值)的影响,在分别检验时这几个因素对于收益率的解释力都很不错,但是在同时回归的时候,发现市值和帐市比中包含了其他几个因素的影响。基于此,两人在一年后推出了神文《Common Risk Factors in Returns on Stocks and Bonds》,并奠定了三因素模型的框架和研究范式。值得一提的是,这篇发在JFE的稿件从收取到录用一共就花了两个月,不得不说大牛就是大牛,另外这篇文献的引用达到恐怖的14000多次。

△Eugene Fama和Kenneth French
这个模型的思路主要由下面这个公式决定:

公式里含有3个贝塔的部分就是模型的三个因子。第一个因子其实和CAPM一致,即投资组合超过市场表现所带来的收益,即超额收益,第二个和第三个因子(分别由市值和帐市比反映)则说明了上市企业的规模和价值都会对投资收益带来影响。
在提取因子的时候,我们需要对数据进行手工的处理,并进行相应的分类。在Fama和French的文章中,他们用每年六月末的股票市值和每年年末的帐市比作为分类依据,因为六月末是美国股市要求披露年报的日期,而年末时间节点的选择是因为我们整个研究是以一个自然年为分组依据。当然在A股的研究中,因为4月是我们年报的披露截止时间,所以在研究中一般会针对市场情况,对时间节点进行调整。
言归正传。第一个步骤是对研究对象进行分组。假如我们要用三因子模型研究沪深300,那么首先我们依据每年4月底的300只股票的实证进行排序,分位值定位50%,也就是说一半小盘股(S)和一半大盘股(B),当然,这个简称不是骂人。然后依据年末的帐市比数据把股票分为三类,30%的高价值(H)、40%的中等价值(M)和30%的低价值(L),然后我们对两类分类法取交集,就可以得到SH、SM、SL、BH、BM和BL六个组合。另外由于我们的研究往往依据多年数据,而上市公司的股票表现都是不断变化的,因此我们需要每十二个月对分组进行一次调整。
另外,我们也需要对六类组合的收益率进行计算,一般我们都是用月数据进行分析,因此我们会使用本月月末的收盘价和上月月末的收盘价作比较计算月收益率,并基于组合中股票市值作为权重指标进行调整,进而得到一个市值加权的收益率,这样我们可以降低极端值的影响。
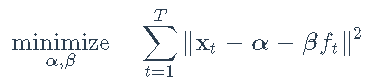
大多数代码行用于准备数据,而不是执行因子建模。让我们开始准备数据:
# 设置开始结束日期和股票名称列表
begin_date <- "2016-01-01"
end_date <- "2017-12-31"
# 从YahooFinance下载数据
data_set <- xts()
for (stock_index in 1:length(stock_namelist))
data_set <- cbind(data_set, Ad(getSymbols(stock_namelist[stock_index],
from = begin_date, to = end_date,
head(data_set)
#> AAPL AMD ADI ABBV AEZS A APD AA CF
#> 2016-01-04 98.74225 2.77 49.99239 49.46063 4.40 39.35598 107.89010 23.00764 35.13227
#> 2016-01-05 96.26781 2.75 49.62508 49.25457 4.21 39.22057 105.96097 21.96506 34.03059
#> 2016-01-06 94.38389 2.51 47.51298 49.26315 3.64 39.39467 103.38042 20.40121 31.08988
#> 2016-01-07 90.40047 2.28 46.30082 49.11721 3.29 37.72138 99.91463 19.59558 29.61520
#> 2016-01-08 90.87848 2.14 45.89677 47.77789 3.29 37.32482 99.39687 19.12169 29.33761
#> 2016-01-11 92.35001 2.34 46.98954 46.25827 3.13 36.69613 99.78938 18.95583 28.14919
head(SP500_index)
#> index
#> 2016-01-04 2012.66
#> 2016-01-05 2016.71
#> 2016-01-06 1990.26
#> 2016-01-07 1943.09
#> 2016-01-08 1922.03
#> 2016-01-11 1923.67
plot(SP500_index) 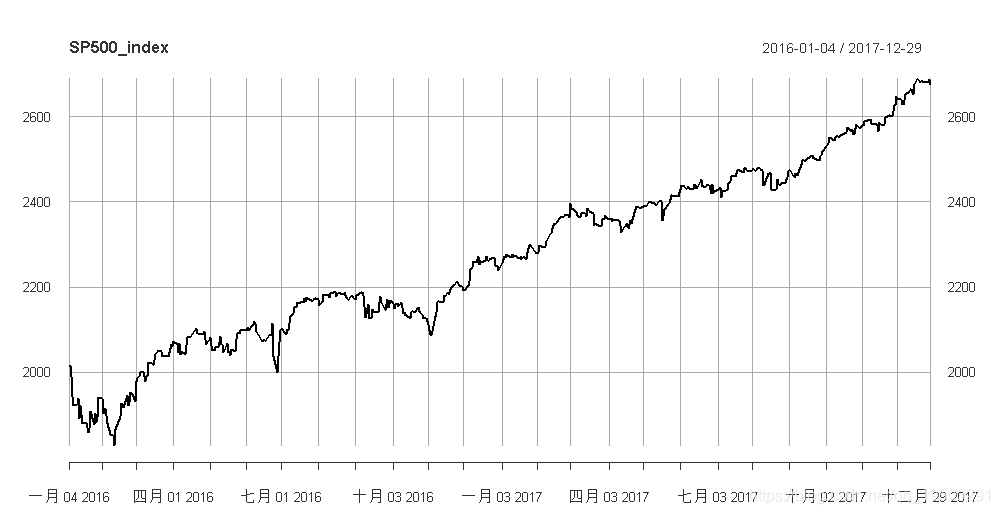
# 计算股票和SP500指数的对数收益率作为显式因子
X <- diff(log(data_set), na.pad = FALSE)
N <- ncol(X) # 股票数量
T <- nrow(X) # 天数 现在我们准备进行因子模型拟合。LS拟合很容易在R中实现,如下所示:

beta <- cov(X,f)/as.numeric(var(f))
alpha <- colMeans(X) - beta*colMeans(f)
sigma2 <- rep(NA, N)
print(alpha)
#> index
#> AAPL 0.0003999086
#> AMD 0.0013825599
#> ADI 0.0003609968
#> ABBV 0.0006684632
#> AEZS -0.0022091301
#> A 0.0002810616
#> APD 0.0001786375
#> AA 0.0006429140
#> CF -0.0006029705
print(beta)
#> index
#> AAPL 1.0957919
#> AMD 2.1738304
#> ADI 1.2683047
#> ABBV 0.9022748
#> AEZS 1.7115761
#> A 1.3277212
#> APD 1.0239453
#> AA 1.8593524
#> CF 1.5702493 或者,我们可以使用矩阵表示法进行拟合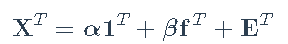
,我们定义
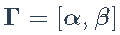
和扩展因子
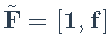
。然后最小化

t(X) %*% F_ %*% solve(t(F_) %*% F_)
#> alpha beta
#> AAPL 0.0003999086 1.0957919
#> AMD 0.0013825599 2.1738304
#> ADI 0.0003609968 1.2683047
#> ABBV 0.0006684632 0.9022748
#> AEZS -0.0022091301 1.7115761
#> A 0.0002810616 1.3277212
#> APD 0.0001786375 1.0239453
#> AA 0.0006429140 1.8593524
#> CF -0.0006029705 1.5702493
E <- xts(t(t(X) - Gamma %*% t(F_)), index(X)) # 残差 另外,我们可以简单地使用R为我们完成工作:
cbind(alpha = factor_model$alpha, beta = factor_model$beta)
#> alpha index
#> AAPL 0.0003999086 1.0957919
#> AMD 0.0013825599 2.1738304
#> ADI 0.0003609968 1.2683047
#> ABBV 0.0006684632 0.9022748
#> AEZS -0.0022091301 1.7115761
#> A 0.0002810616 1.3277212
#> APD 0.0001786375 1.0239453
#> AA 0.0006429140 1.8593524
#> CF -0.0006029705 1.5702493 可视化协方差矩阵
有趣的是,可视化对数收益率[算术处理误差]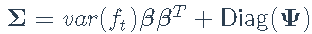
以及残差Ψ的估计协方差矩阵。让我们从对数收益率的协方差矩阵开始:
main = "单因子模型对数收益的协方差矩阵") 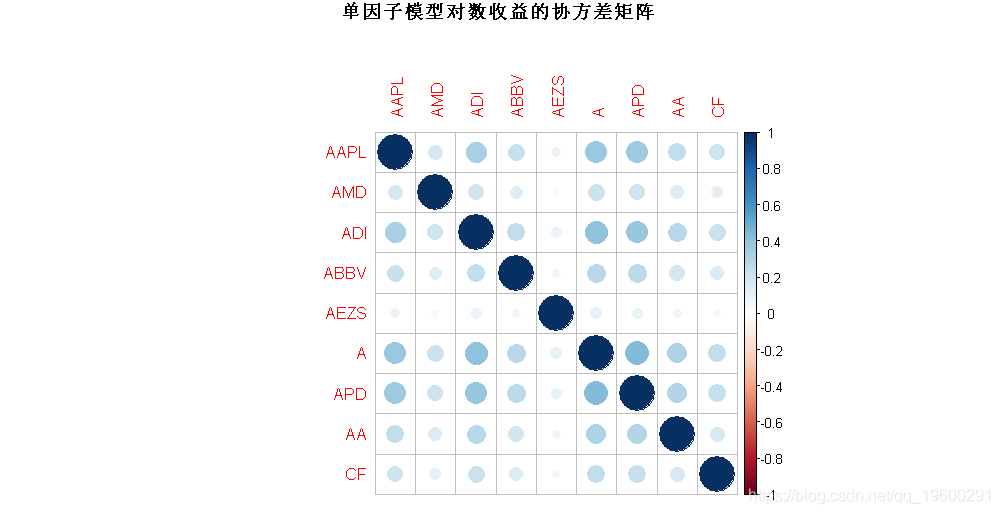
我们可以观察到所有股票都是高度相关的,这是市场因素的影响。为了检查股票相关关系,我们绘制相关图:
plot(cov2cor(Psi),
main = "残差协方差矩阵") 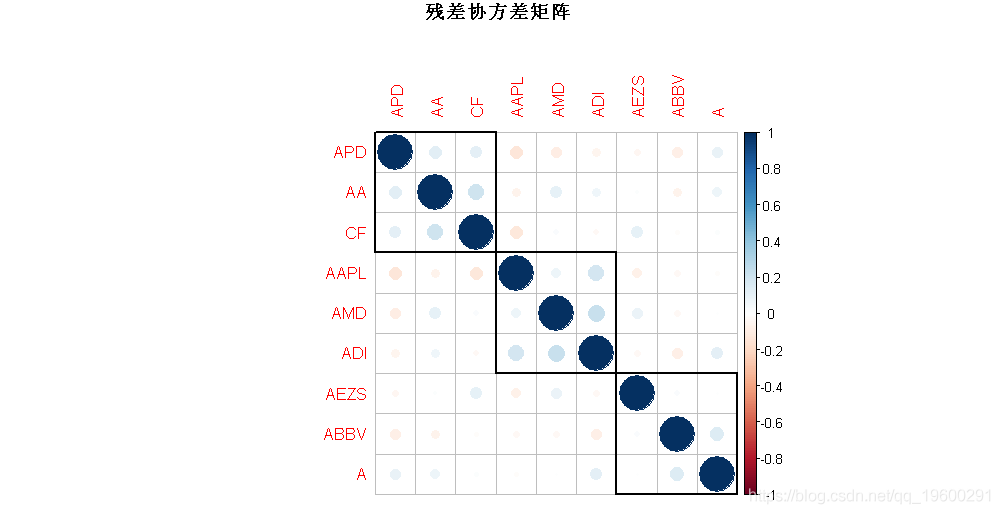
cbind(stock_namelist, sector_namelist) # 股票的行业
#> stock_namelist sector_namelist
#> [1,] "AAPL" "Information Technology"
#> [2,] "AMD" "Information Technology"
#> [3,] "ADI" "Information Technology"
#> [4,] "ABBV" "Health Care"
#> [5,] "AEZS" "Health Care"
#> [6,] "A" "Health Care"
#> [7,] "APD" "Materials"
#> [8,] "AA" "Materials"
#> [9,] "CF" "Materials" 随时关注您喜欢的主题
有趣的是,我们可以观察到对Ψ执行的自动聚类可以正确识别股票的行业。
评估投资资金
在此示例中,我们将基于因子模型评估几种投资基金的绩效。我们将标准普尔500指数作为明确的市场因素,并假设无风险收益为零 rf = 0。特别是,我们考虑六种交易所买卖基金(ETF):
我们首先加载数据:
# 设置开始结束日期和股票名称列表
begin_date <- "2016-10-01"
end_date <- "2017-06-30"
# 从YahooFinance下载数据
data_set <- xts()
for (stock_index in 1:length(stock_namelist))
data_set <- cbind(data_set, Ad(getSymbols(stock_namelist[stock_index],
head(data_set)
#> SPY XIVH SPHB SPLV USMV JKD
#> 2016-10-03 203.6610 29.400 31.38322 38.55683 42.88382 119.8765
#> 2016-10-04 202.6228 30.160 31.29729 38.10687 42.46553 119.4081
#> 2016-10-05 203.5195 30.160 31.89880 38.02249 42.37048 119.9421
#> 2016-10-06 203.6610 30.160 31.83196 38.08813 42.39899 120.0826
#> 2016-10-07 202.9626 30.670 31.58372 37.98500 42.35146 119.8296
#> 2016-10-10 204.0197 31.394 31.87970 38.18187 42.56060 120.5978
head(SP500_index)
#> index
#> 2016-10-03 2161.20
#> 2016-10-04 2150.49
#> 2016-10-05 2159.73
#> 2016-10-06 2160.77
#> 2016-10-07 2153.74
#> 2016-10-10 2163.66
# 计算股票和SP500指数的对数收益率作为显式因子
X <- diff(log(data_set), na.pad = FALSE)
N <- ncol(X) # 股票数量
T <- nrow(X) # 天数 现在我们可以计算所有ETF的alpha和beta:
#> alpha beta
#> SPY 7.142225e-05 1.0071424
#> XIVH 1.810392e-03 2.4971086
#> SPHB -2.422107e-04 1.5613533
#> SPLV 1.070918e-04 0.6777149
#> USMV 1.166177e-04 0.6511667
#> JKD 2.569578e-04 0.8883843 现在可以进行一些观察:
- SPY是S&P 500的ETF,如预期的那样,其alpha值几乎为零,beta值几乎为1: α= 7.142211×10-5和 β= 1.0071423。
- XIVH是具有高alpha值的ETF,计算出的alpha值是ETF中最高的(高1-2个数量级): α= 1.810392×10-3。
- SPHB是一种ETF,据推测具有很高的beta,而计算出的beta却是最高的,但不是最高的:β= 1.5613531。有趣的是,计算出的alpha为负,因此,该ETF应谨慎。
- SPLV是降低波动性的ETF,实际上,计算得出的beta偏低:β= 0.6777072。
- USMV还是降低波动性的ETF,实际上,计算出的beta是最低的:β= 0.6511671。
- JKD显示出很好的折衷。
我们可以使用一些可视化:
barplot(rev(alpha), horiz = TRUE, main = "alph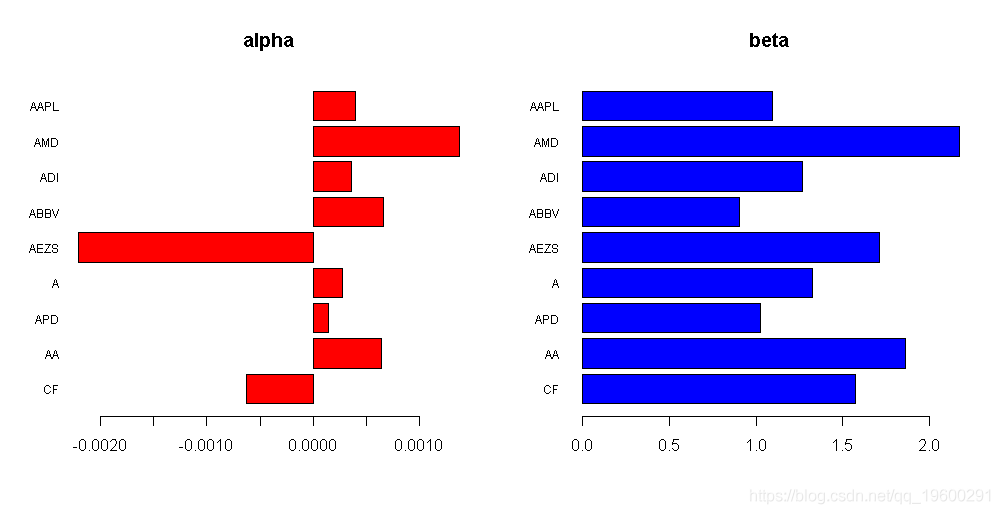
我们还可以使用例如Sharpe比率,以更系统的比较不同的ETF。回顾一种资产和一个因素的因子模型
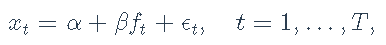
我们获得
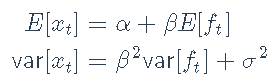
夏普比率如下: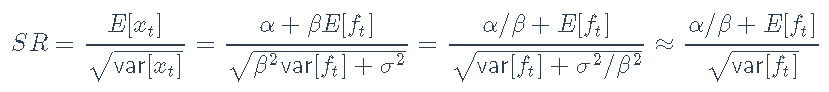
假设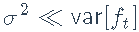
。因此,基于Sharpe比率对不同资产进行排名的一种方法是根据α/β比率对它们进行排名:
print(ranking)
#> alpha/beta SR alpha beta
#> XIVH 7.249952e-04 0.13919483 1.810392e-03 2.4971086
#> JKD 2.892417e-04 0.17682677 2.569578e-04 0.8883843
#> USMV 1.790904e-04 0.12280053 1.166177e-04 0.6511667
#> SPLV 1.580189e-04 0.10887903 1.070918e-04 0.6777149
#> SPY 7.091574e-05 0.14170591 7.142225e-05 1.0071424
#> SPHB -1.551287e-04 0.07401566 -2.422107e-04 1.5613533 可以看到:
- 就α/β而言,XIVH最佳(α最大),而SPHB最差(α负)。
- 就夏普比率(更确切地说,是信息比率,因为我们忽略了无风险利率)而言,JDK是最好的,其次是SPY。这证实了大多数投资基金的表现不超过市场的观点。
- 显然,无论以哪种衡量标准,SPHB都是最差的:负α,负β比率和Sharpe比率。
- JDK之所以能够取得最佳性能,是因为它的alpha值很好(尽管不是最好的),而同时具有0.88的中等beta值。
- XIVH和SPHB有大量不同的beta,因此在市场上具有极端敞口。
- USMV在市场上的曝光率最小,有可接受的alpha值,并且其Sharpe比率接近第二和第三高的位置。
Fama-French三因子模型
该示例将说明使用标准普尔500指数中的九种股票的Fama-French三因子模型。让我们从加载数据开始:
# 设置开始结束日期和股票名称列表
begin_date <- "2013-01-01"
end_date <- "2017-08-31"
# 从YahooFinance下载数据
data_set <- xts()
for (stock_index in 1:length(stock_namelist))
data_set <- cbind(data_set, Ad(getSymbols(stock_namelist[stock_index],
# 下载Fama-French因子
head(fama_lib)
#> Mkt.RF SMB HML
#> 1926-07-01 0.10 -0.24 -0.28
#> 1926-07-02 0.45 -0.32 -0.08
#> 1926-07-06 0.17 0.27 -0.35
#> 1926-07-07 0.09 -0.59 0.03
#> 1926-07-08 0.21 -0.36 0.15
#> 1926-07-09 -0.71 0.44 0.56
tail(fama_lib)
#> Mkt.RF SMB HML
#> 2017-11-22 -0.05 0.10 -0.04
#> 2017-11-24 0.21 0.02 -0.44
#> 2017-11-27 -0.06 -0.36 0.03
#> 2017-11-28 1.06 0.38 0.84
#> 2017-11-29 0.02 0.04 1.45
#> 2017-11-30 0.82 -0.56 -0.50
# 计算股票的对数收益率和Fama-French因子
X <- diff(log(data_set), na.pad = FALSE)
N <- ncol(X) #股票数量 现在我们在矩阵F中具有三个因子,并希望拟合模型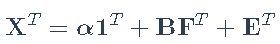
,其中现在的载荷是一个beta矩阵:
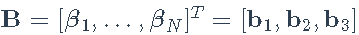
。我们可以做最小二乘拟合,最小化
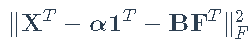
。更方便地,我们定义
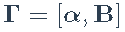
和扩展因子
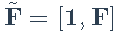
。然后可以将LS公式写为最小化

print(Gamma)
#> alpha b1 b2 b3
#> AAPL 1.437845e-04 0.9657612 -0.23339130 -0.49806858
#> AMD 6.181760e-04 1.4062105 0.80738336 -0.07240117
#> ADI -2.285017e-05 1.2124008 0.09025928 -0.20739271
#> ABBV 1.621380e-04 1.0582340 0.02833584 -0.72152627
#> AEZS -4.513235e-03 0.6989534 1.31318108 -0.25160182
#> A 1.146100e-05 1.2181429 0.10370898 -0.20487290
#> APD 6.281504e-05 1.0222936 -0.04394061 0.11060938
#> AA -4.587722e-05 1.3391852 0.62590136 0.99858692
#> CF -5.777426e-04 1.0387867 0.48430007 0.82014523 另外,我们可以使用R完成:
#> alpha Mkt.RF SMB HML
#> AAPL 1.437845e-04 0.9657612 -0.23339130 -0.49806858
#> AMD 6.181760e-04 1.4062105 0.80738336 -0.07240117
#> ADI -2.285017e-05 1.2124008 0.09025928 -0.20739271
#> ABBV 1.621380e-04 1.0582340 0.02833584 -0.72152627
#> AEZS -4.513235e-03 0.6989534 1.31318108 -0.25160182
#> A 1.146100e-05 1.2181429 0.10370898 -0.20487290
#> APD 6.281504e-05 1.0222936 -0.04394061 0.11060938
#> AA -4.587722e-05 1.3391852 0.62590136 0.99858692
#> CF -5.777426e-04 1.0387867 0.48430007 0.82014523 统计因子模型
现在让我们考虑统计因子模型或隐式因子模型,其中因子和载荷均不可用。调用具有 K因子的模型 XT =α1T+ BFT + ET的主成分方法:
- PCA:
- 样本均值:
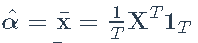
- 矩阵:
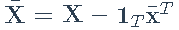
- 样本协方差矩阵:
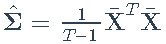
- 特征分解:
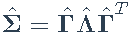
- 样本均值:
- 估计:
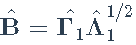
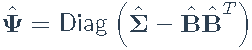
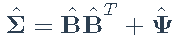
- 更新特征分解:
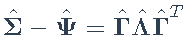
- 重复步骤2-3,直到收敛为止。
#> alpha
#> AAPL 0.0007074564 0.0002732114 -0.004631647 -0.0044814226
#> AMD 0.0013722468 0.0045782146 -0.035202146 0.0114549515
#> ADI 0.0006533116 0.0004151904 -0.007379066 -0.0053058139
#> ABBV 0.0007787929 0.0017513359 -0.003967816 -0.0056000810
#> AEZS -0.0041576357 0.0769496344 0.002935950 0.0006249473
#> A 0.0006902482 0.0012690079 -0.005680162 -0.0061507654
#> APD 0.0006236565 0.0005442926 -0.004229364 -0.0057976394
#> AA 0.0006277163 0.0027405024 -0.009796620 -0.0149177957
#> CF -0.0000573028 0.0023108605 -0.007409061 -0.0153425661 同样,我们可以使用R完成工作:
#> alpha factor1 factor2 factor3
#> AAPL 0.0007074564 0.0002732114 -0.004631647 -0.0044814226
#> AMD 0.0013722468 0.0045782146 -0.035202146 0.0114549515
#> ADI 0.0006533116 0.0004151904 -0.007379066 -0.0053058139
#> ABBV 0.0007787929 0.0017513359 -0.003967816 -0.0056000810
#> AEZS -0.0041576357 0.0769496344 0.002935950 0.0006249473
#> A 0.0006902482 0.0012690079 -0.005680162 -0.0061507654
#> APD 0.0006236565 0.0005442926 -0.004229364 -0.0057976394
#> AA 0.0006277163 0.0027405024 -0.009796620 -0.0149177957
#> CF -0.0000573028 0.0023108605 -0.007409061 -0.0153425661 我们最终将比较以下不同的因子模型:
- 样本协方差矩阵
- 宏观经济一因素模型
- 基本的三因素Fama-French模型
- 统计因素模型
我们在训练阶段估计模型,然后将估计的协方差矩阵与测试阶段的样本协方差矩阵进行比较。估计误差将根据PRIAL(平均损失提高百分比)进行评估:
通过不同因子模型进行协方差矩阵估计的最终比较
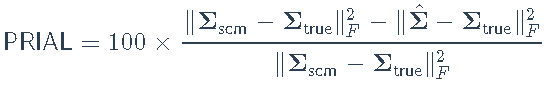
加载训练和测试集:
# 设置开始结束日期和股票名称列表
begin_date <- "2013-01-01"
end_date <- "2015-12-31"
# 准备股票数据
data_set <- xts()
for (stock_index in 1:length(stock_namelist))
data_set <- cbind(data_set, Ad(getSymbols(stock_namelist[stock_index],
# Fama-French 因子
mydata <- mydata[-nrow(mydata),
# 准备指数
f_SP500 <- diff(log(SP500_index), na.pad = FALSE)
# 将数据拆分为训练数据和测试数据
T_trn <- round(0.45*T)
X_trn <- X[1:T_trn, ]
X_tst <- X[(T_trn+1):T, ] 现在让我们用训练数据估算不同的因子模型:
# 样本协方差矩阵
Sigma_SCM <- cov(X_trn)
# 单因素模型
Gamma <- t(solve(t(F_) %*% F_, t(F_) %*% X_trn))
E <- xts(t(t(X_trn) - Gamma %*% t(F_)), index(X_trn))
# Fama-French三因子模型
Sigma_FamaFrench <- B %*% cov(F_FamaFrench_trn) %*% t(B) + diag(diag(Psi))
# 统计单因子模型
while (norm(Sigma - Sigma_prev, "F")/norm(Sigma, "F") > 1e-3) {
B <- eigSigma$vectors[, 1:K, drop = FALSE] %*% diag(sqrt(eigSigma$values[1:K]), K, K)
# 统计三因子模型
K <- 3
while (norm(Sigma - Sigma_prev, "F")/norm(Sigma, "F") > 1e-3) {
B <- eigSigma$vectors[, 1:K] %*% diag(sqrt(eigSigma$values[1:K]), K, K)
Psi <- diag(diag(Sigma - B %*% t(B)))
Sigma_PCA3 <- Sigma
# 统计五因子模型
K <- 5
eigSigma <- eigen(Sigma)
while (norm(Sigma - Sigma_prev, "F")/norm(Sigma, "F") > 1e-3) {
B <- eigSigma$vectors[, 1:K] %*% diag(sqrt(eigSigma$values[1:K]), K, K)
Psi <- diag(diag(Sigma - B %*% t(B))) 最后,让我们比较测试数据中的不同估计:
Sigma_true <- cov(X_tst)
barplot(error, main = "协方差矩阵估计误差", 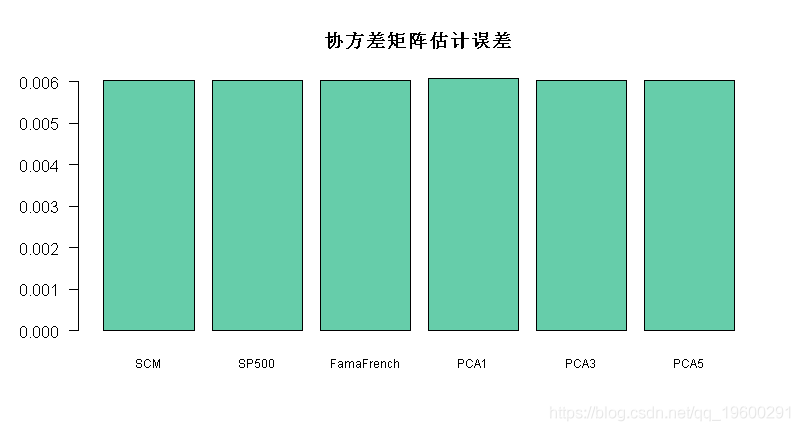
PRIAL <- 100*(ref - error^2)/ref
barplot(PRIAL, main = "协方差矩阵估计的先验方法", 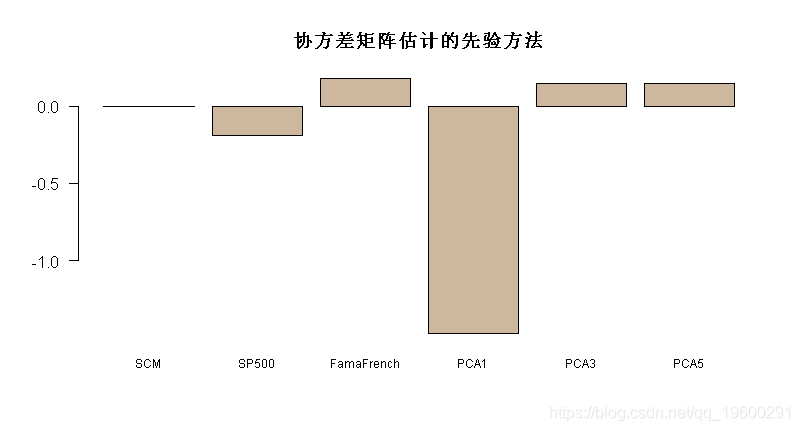
最终可以看到使用因子模型进行协方差矩阵估计会有所帮助。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 2026脑机接口行业深度报告:市场规模、产业链、临床进展、政策赋能|附50+份报告PDF、数据、可视化模板汇总下载
2026脑机接口行业深度报告:市场规模、产业链、临床进展、政策赋能|附50+份报告PDF、数据、可视化模板汇总下载 Python用Seedream4.5图像生成模型API调用与多场景应用|附代码教程
Python用Seedream4.5图像生成模型API调用与多场景应用|附代码教程 R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据
R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据 R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据
R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据



