
本文将使用一个小数据说明ROC曲线,其中n = 10个观测值,两个连续变量x_1和x_2,以及二元变量y∈{0,1}。
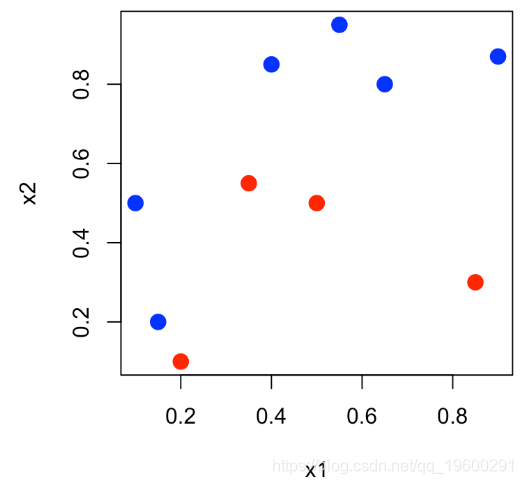
我们可以表示平面(x_1,x_2)中的点,并且对y∈{0,1}中的y 使用不同的颜色。
df = data.frame(x1=x1,x2=x2,y=as.factor(y))
plot(x1,x2,col=c("red","blue")[1+y],pch=19,cex=1.5)可下载资源
然后,我们可以进行逻辑回归,P(Y = 1∣x1,x2)= 1 +eβ0+β1×1 +β2x2eβ0+β1×1 +β2×2 ,
受试者工作特征曲线 (receiver operating characteristic curve,简称ROC曲线),又称为感受性曲线(sensitivity curve)。得此名的原因在于曲线上各点反映着相同的感受性,它们都是对同一信号刺激的反应,只不过是在几种不同的判定标准下所得的结果而已。为了了解ROC曲线的意义,我们首先得了解一些变量。以下定义引自维基百科Receiver operating characteristic,其中1代表正,0代表负。
condition positive (P)
the number of real positive cases in the data(数据中的所有1)
condition negatives (N)
the number of real negative cases in the data(数据中所有的0)
true positive (TP)
eqv. with hit(被判断为1的1,即1中判断正确的量)
true negative (TN)
eqv. with correct rejection(被判断为0的0,即0中判断正确的量)
false positive (FP)
eqv. with false alarm, Type I error(被判断为1的0,即第一类错误)
false negative (FN)
eqv. with miss, Type II error(被判断为0的1,即第二类错误)
sensitivity, recall, hit rate, or true positive rate (TPR)
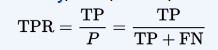
fall-out or false positive rate (FPR)
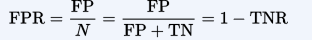
specificity or true negative rate (TNR)
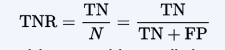
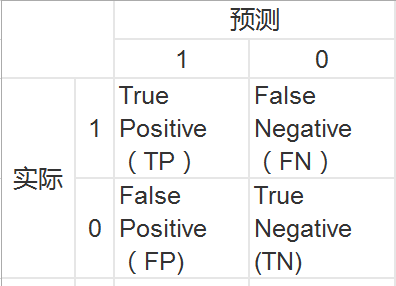
举例来讲,对于一个二分问题,可将实例(case)分成正类(positive)或负类(negative)。如果进行预测,会出现四种情况,即:实例是正类并且也被预测成正类,即为真正类TP(True positive),实例是负类被预测成正类,称之为假正类FP(False positive),实例是负类被预测成负类,称之为真负类TN(True negative),实例是正类被预测成负类,称之为假负类FN(false negative)。列表如下表所示,其中1代表正类,0代表负类
经过上面的说明我们知道,ROC曲线的横坐标和纵坐标其实是没有相关性的,所以不能把ROC曲线当做一个函数曲线来分析,应该把ROC曲线看成无数个点,每个点都代表一个分类器,其横纵坐标表征了这个分类器的性能。为了更好的理解ROC曲线,我们先引入ROC空间,如下图所示。
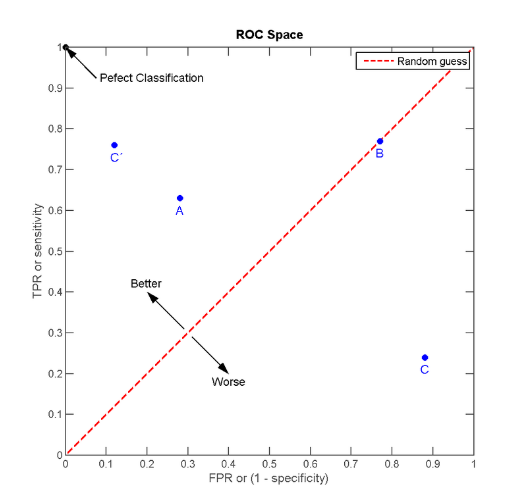
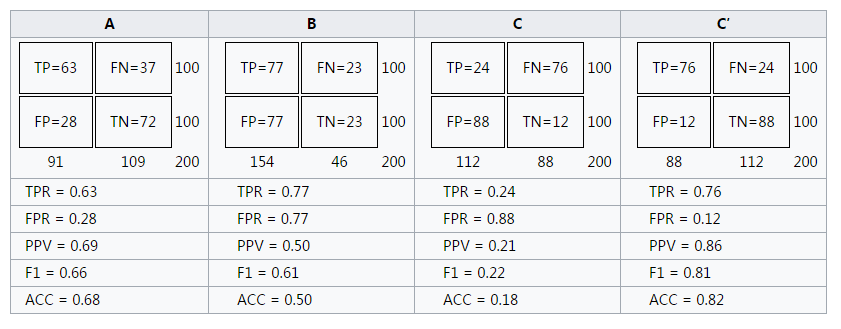
明显的,C'的性能最好。而B的准确率只有0.5,几乎是随机分类。特别的,图中左上角坐标为(1,0)的点为完美分类点(perfect classification),它代表所有的分类全部正确,即归为1的点全部正确(TPR=1),归为0的点没有错误(FPR=0)。
通过ROC空间,我们明白了一条ROC曲线其实代表了无数个分类器。那么我们为什么常常用一条ROC曲线来描述一个分类器呢?仔细观察ROC曲线,发现其都是上升的曲线(斜率大于0),且都通过点(0,0)和点(1,1)。其实,这些点代表着一个分类器在不同阈值下的分类效果,具体的,曲线从左往右可以认为是阈值从0到1的变化过程。当分类器阈值为0,代表不加以识别全部判断为0,此时TP=FP=0,TPR=TP/P=0,FPR=FR/N=0;当分类器阈值为1,代表不加以识别全部判断为1,此时FN=TN=0,P=TP+FN=TP, TPR=TP/P=1,N=FP+TN=FP, FPR=FR/N=1。所以,ROC曲线描述的其实是分类器性能随着分类器阈值的变化而变化的过程。对于ROC曲线,一个重要的特征是它的面积,面积为0.5为随机分类,识别能力为0,面积越接近于1识别能力越强,面积等于1为完全识别。
reg = glm(y~x1+x2,data=df,family=binomial(link = "logit"))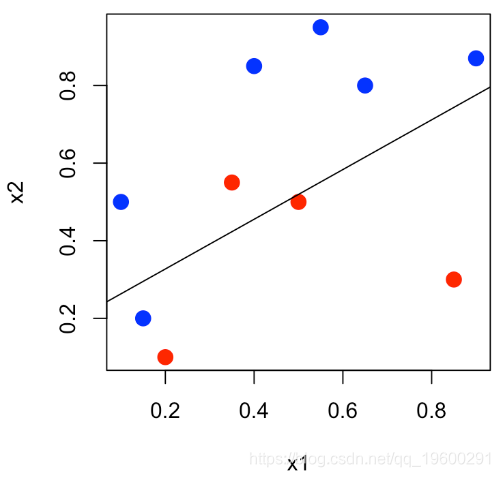
然后我们可以将y_i表示为得分的函数,即P(Y = 1∣x1,i ,x2,i),
S = predict(reg,type="response")
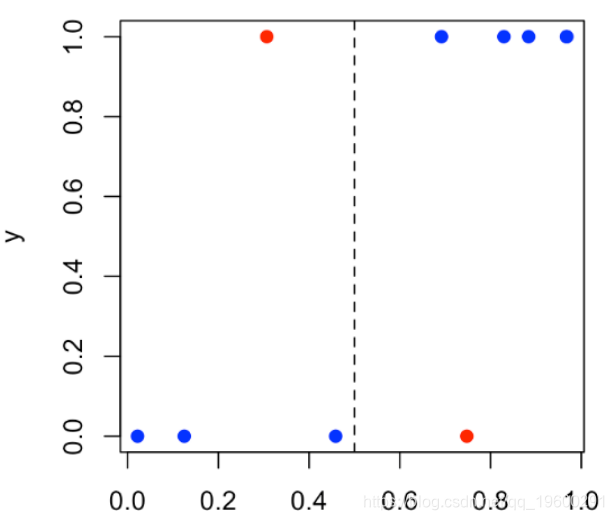
plot(S,y )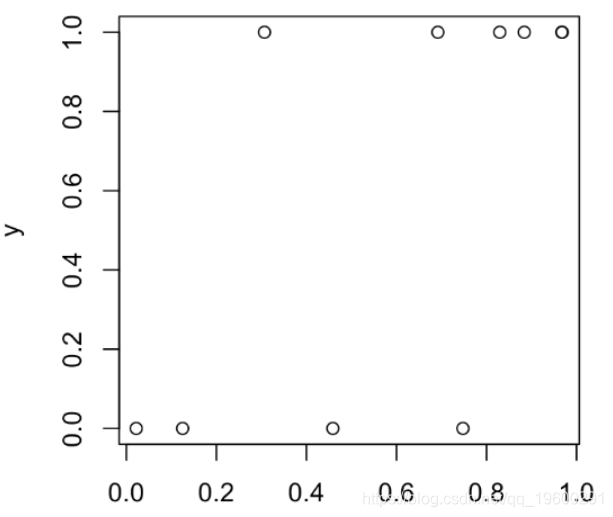
然后,我们将设定一个阈值(例如50%):如果Y取值1的概率超过阈值,我们将预测为1(否则为0)。在上图中,我们有4个点:阈值左侧的那些点(预测为0),如果位于底部,则分类很好,而位于顶部的分类很差;在阈值的右边(并且预测为1),如果它们位于顶部,则可以很好地分类,而底部则不能很好地分类
plot(S,y,
col=c("red","blue")[1+(y==Yhat)])
abline(v=s,lty=2)
颜色反映了分类的好坏:红点表示分类错误。我们可以在 下面的列联表(混淆矩阵)中找到所有这些内容 。
Y Yhat 0 1
0 3 1
1 1 5
在这里,我们感兴趣的是两个指标:假正例和真正例,
FP=sum((Ps==1)*(Y==0))/sum(Y==0)
TP=sum((Ps==1)*(Y==1))/sum(Y==1)我们在给定的阈值(此处为50 %)处获得了该表。
这组结果给出了ROC曲线。
plot(t(V),type="s" )
segments(0,0,1,1,col="light blue")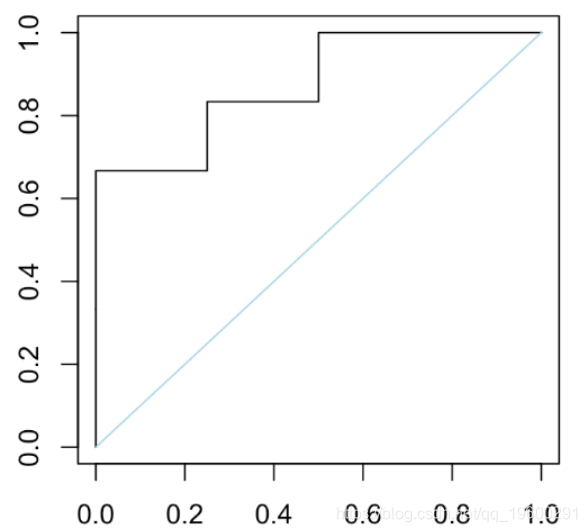
我们可以检查在曲线上阈值50%处的点
Y Yhat 0 1
0 3 1
1 1 5
(FP = sum((Yhat)*(Y==0))/sum(Y==0))
[1] 0.25
(TP = sum((Yhat==1)*(Y==1))/sum(Y==1))
[1] 0.83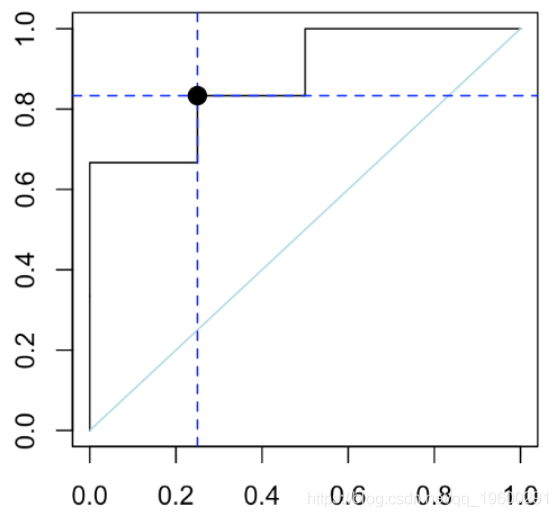
plot(performance(pred,"tpr","fpr"))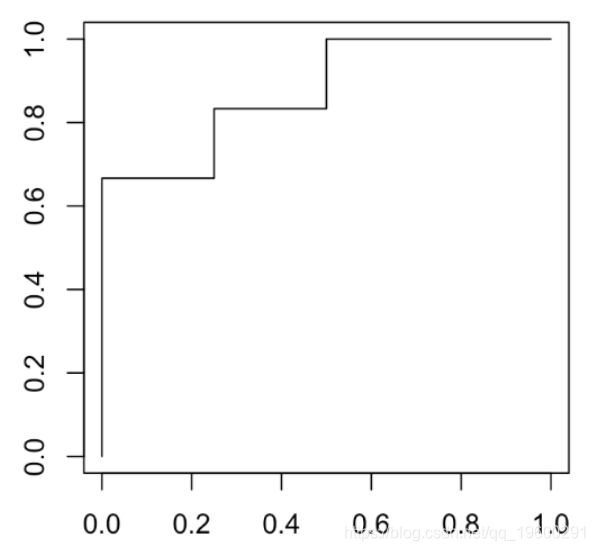
一个有趣的量称为曲线下面积(或 AUC),可在此处手动计算(我们有一个简单的阶梯函数)
p2[1]*p2[2]+(p1[1]-p2[1])*p1[2]+(1-p1[1])
[1] 0.875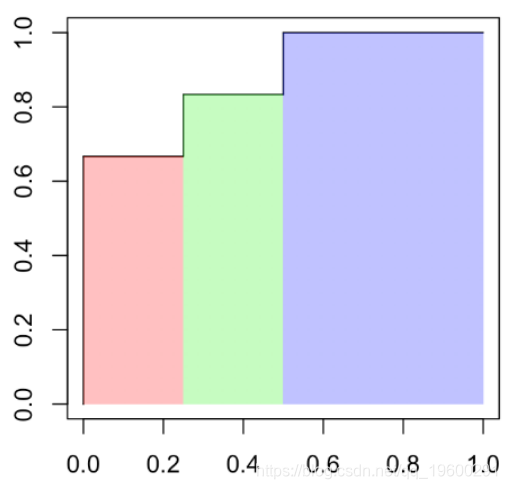
也可以用函数计算
auc.perf@y.values[[1]]
[1] 0.87我们尝试另一个分类器:仍然是逻辑回归,但要考虑通过将第二个变量分割成两个而获得的因子1 [s,∞) x2)
abline(h=.525)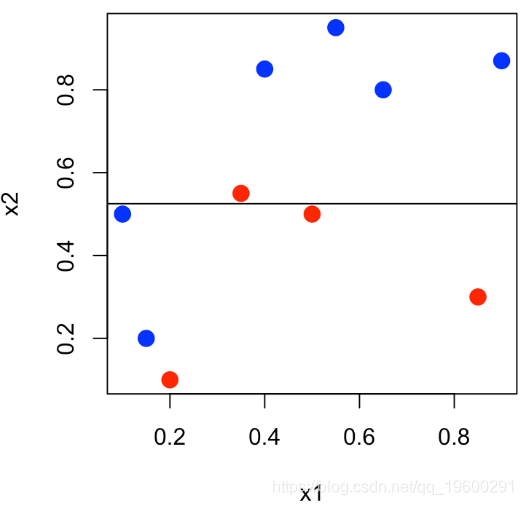
水平线不再是红色和蓝色一样多的线,而是与变量x_2相交的线。在这里,我们仅预测两个值:底部出现蓝色的概率为40%,顶部为蓝色的概率为80%。如果我们将观测值yi表示为预测概率的函数,则可以得出
plot(S,y,ylab="y",xlim=0:1)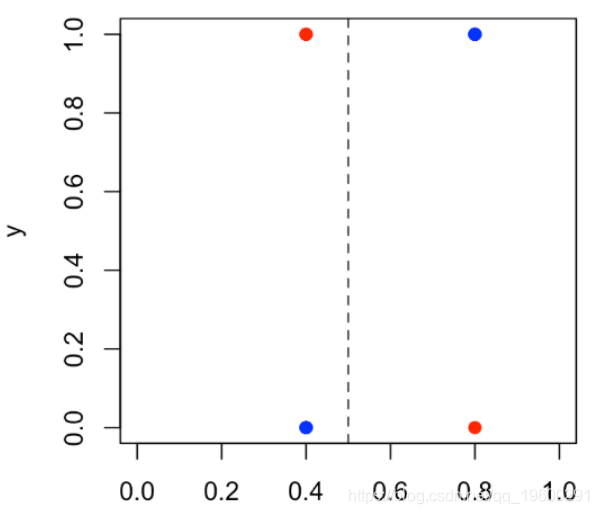
50%的阈值,我们获得以下列联表
Y Yhat 0 1
0 3 2
1 1 4
如果绘制ROC曲线,我们得到
plot(t(V),type="l"
segments(0,0,1,1,col="light blue")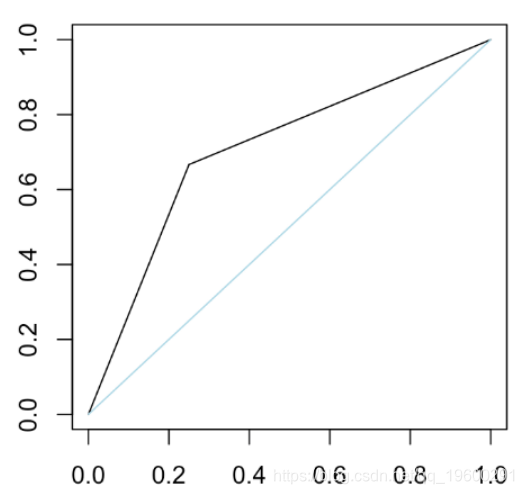
这次,曲线是线性的。上图中的蓝色对角线恰好是随机分类器,这是我们随机预测的结果
pred = prediction(S,Y)
plot(performance(pred,"tpr","fpr"))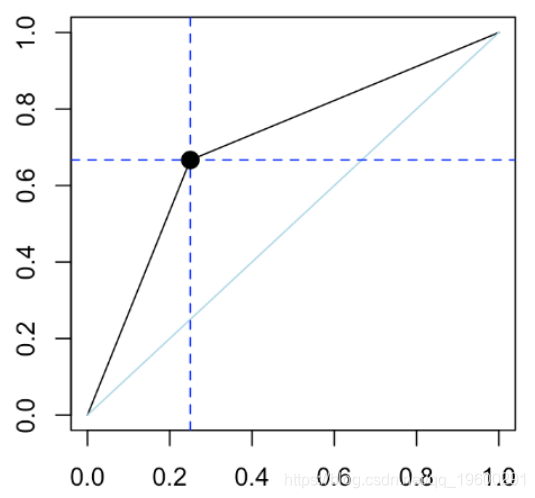
该点的阈值为50%。再次,我们可以计算曲线下的面积
p2[1]*p2[2]/2+(1-p1[1])*p1[2]+(1-p1[1])*(1-p1[2])/2
[1] 0.708
auc.perf@y.values[[1]]
[1] 0.708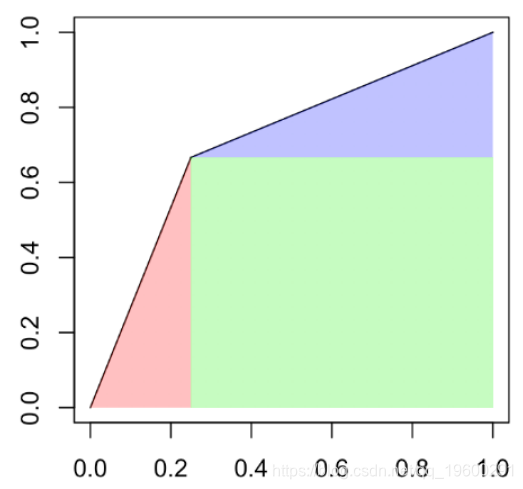



 Python用PSO优化SVM与RBFN在自动驾驶系统仿真、手写数字分类应用研究
Python用PSO优化SVM与RBFN在自动驾驶系统仿真、手写数字分类应用研究 视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析
视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析 MATLAB用CNN-LSTM神经网络的语音情感分类深度学习研究
MATLAB用CNN-LSTM神经网络的语音情感分类深度学习研究



