在这篇文章中,我使用 R 建立著名的Hull-White利率模型并进行仿真。
最近我们被客户要求撰写关于Hull White短期利率模型的研究报告,包括一些图形和统计输出。Hull and White(1994)模型解决Vasicek模型对利率的初始期限结构的拟合不佳的问题。该模型定义为:
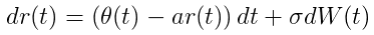
Wt是风险中性框架下的维纳过程,模拟随机市场风险因素。σ是标准差参数,影响利率的波动,波动幅度有着瞬时随机流动的特征。
|
Vasicek Model 是个Short Rate 模型,只要制定三个参数,就可以对Short Rate进行模拟。
dr(t+1)=a(b-r(t))+sigma*dZ a:为回归速度的参数 b:长期回归利率值 sigma:为short Rate的波动率 一般来说,r(0)可以用隔夜的shibor来approx b 可以设置为到期日期限很长的利率 a是用于设置曲线由多快从近期的利率点回归到长期的利率点,这你就要根据实际利率曲线的特征 做一些测算。 sigma:也和a有类似的效果,更多的来影响不同节点利率的波动区间,所以你仍旧需要根据利率的实证数据做测算。 Vasicek 有几个特性,首先 Short Rate是一个不可观察值,你可以假设给某人放贷,但是放贷时间近似于无限小。所以在你对Short Rate进行模拟后,还需要根据Short Rate的路径重组利率曲线。 其次,你也可以通过Vasicek的P(t,T)的公式来计算在不同时点债券的价格,这是Vasicek的优势,简便但是他在Curve Fitting 上无法满足与市场曲线保持一致,这是他的弊端,所以也通常被称之为均衡模型而非无风险套利模型。如果从风险管理的角度来说的话,Vasicek是可以有效解释曲线的变动的,所以只要不是用户产品定价,这个模型在一定程度上还是可用的。 最后,就是这个模型遵循布朗运动的正态分布,所以有可能会出现负值。所以对于日本这种利率较低的经济体系,这个模型特别的不好用。 |
参数b,a,σ和初始条件r0是完全动态的,并且瞬时变动。该模型的另一种示形式是:
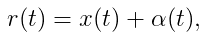
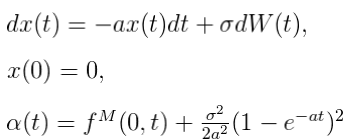
假定a是非负数:
b:长期平均水平。在长期水平下产生一系列r的轨道值。
a:回归速度。代表b的轨道值实时重组的速度。
σ:代表瞬时波动,测量每个时点随机因素进入系统的振幅。
以下是由公式导出的一些数值:
![]() :长期方差。计算在长期所有r值围绕平均值重组的轨道值。
:长期方差。计算在长期所有r值围绕平均值重组的轨道值。
a与σ数值相反波动:增加σ会增加随机数进入系统的数量,
当a增加会使方差稳定,围绕长期平均值b以方差值波动。这在看长期方差时十分明显。 当方差值不变时,若σ增加,a减少。此模型是一个奥恩斯坦 – 乌伦贝克随机过程。
这些假设以及 对信贷/流动性风险的简单(并行)调整仍在保险中广泛使用 ,但在2007年次贷危机后被市场抛弃。
有关新的多曲线方法的更多详细信息,请参见例如 http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2219548。在本文中,作者介绍了一个多曲线自举(bootstrap)过程。
#清理工作区
rm(list=ls())#模拟的频率
freq <- "monthly"
delta_t <- 1/12#数据
params <- list(tradeDate=as.Date('2002-2-15'),
settleDate=as.Date('2002-2-19'),
payFixed=TRUE,
dt=delta_t,
strike=.06,
method="HWAnalytic",
interpWhat="zero",
interpHow= "spline")#构建利率期限结构的市场数据
#存款和掉期
tsQuotes <- list(d1w =0.0382,
s2y = 0.037125,
s3y =0.0398,#具有相应期限和期限的掉期波动率矩阵
swaptionMaturities <- c(1:5)
swapTenors <- c(1:5)
#为掉期定价
pric <- Swaption(params, swaptionMaturities, swapTenors,
#构建利率的即期期限结构
#根据输入的市场数据
times <- seq(from = delta_t, to = 5, by = delta_t)
maturities <- curves$times
############## Hull-White短期利率模拟
#模拟次数,频率
horizon <- 5
sims <- 10000#校准Hull-White参数
a <- pricing$a
sigma <- pricing$sigma#使用模拟高斯冲击
simshos(n = nb.sims, horizon = horizon )#使用模拟因子x
#我使用远期汇率。由于每月的频率较低,
#我认为它们是瞬时远期汇率
fwdrates <- ts(replicate(nb.sims, curves$forwards),
start = start(x),
deltat = deltat(x))# α
alpha <- fwdrates + param.alpha#短期利率
r <- x + alpha#随机贴现因子(当前的数值积分是非常基本的)
#由随机贴现因子得出的蒙特卡洛价格和零利率
montecarlozerorates <- -log(montecarloprices)/maturities #市场和蒙特卡洛价格之间的差异的置信区间
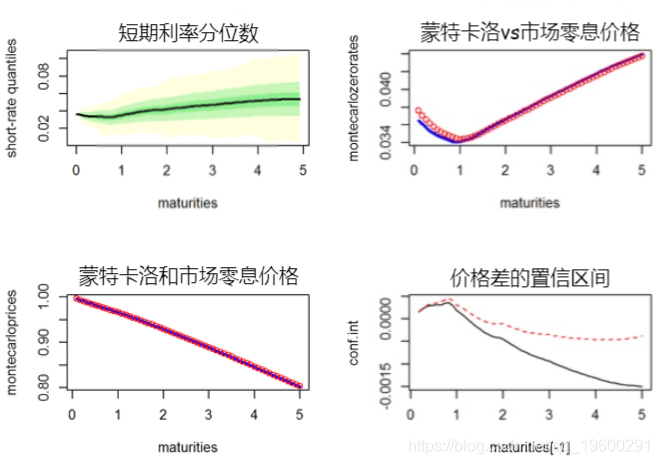
conf.int <- t(apply((Dt - marketprices)[-1, ], 1, function(x) t.test(x)$conf.int)) par(mfrow = c(2, 2)) #短期利率分位数
#蒙特卡洛vs市场零利率
plot(maturities, montecarlozerorates, type='l', col = 'blue', lwd = 3,
points(maturities, marketzerorates, col = 'red')#蒙特卡洛vs市场零息价格
plot(maturities, montecarloprices, type ='l', col = 'blue', lwd = 3,
points(maturities, marketprices, col = 'red')#价格差的置信区间
matplot(maturities[-1], conf.int, type = 'l',
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 Python用PSO优化SVM与RBFN在自动驾驶系统仿真、手写数字分类应用研究
Python用PSO优化SVM与RBFN在自动驾驶系统仿真、手写数字分类应用研究 视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析
视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析 高维变量选择专题|R、Python用HOLP、Lasso、SCAD、PCR、ElasticNet实例合集分析企业财务、糖尿病、基因数据
高维变量选择专题|R、Python用HOLP、Lasso、SCAD、PCR、ElasticNet实例合集分析企业财务、糖尿病、基因数据



