本文通过R语言建立广义线性模型(GLM)、多项式回归和广义可加模型(GAM)来预测谁在1912年的泰坦尼克号沉没中幸存下来。
我们读取泰坦尼克号数据集 ,并查看数据结构
str(titanic)数据变量为:
Survived:乘客存活指标(如果存活则为1)Pclass:旅客舱位等级Sex:乘客性别Age:乘客年龄SibSp:兄弟姐妹/配偶人数Parch:父母/子女人数Embarked: 登船港口Name:旅客姓名
线性模型简单、直观、便于理解,但是现实中,线性假设很可能不能满足实际需求,甚至直接违背实际情况。但我们可以通过一种方式来改善模型,那就是改变”线性假设”。接下来,我们介绍一些由线性假设下,扩展得到的其他模型。
一,多项式回归
在了解简单线性模型的基础上,很容易理解多项式回归,形如:
其中,为误差项
多项式回归的优点是,随着变量的增加,可以拟合出异常极端变化的曲线。不过通常来说,多项式回归基本都不会超过四项式。
二,分段常值函数(step functions)
不论简单线性回归、多项式回归等都是具有全局性的结构。再不考虑全局性回归时,可以用到分段回归。
最简单的分段回归应该就是形如阶跃函数了,阶跃函数也是提供连续变量离散化成有序分类变量的方法。
过程如下:
对X进行分组;
每个组拟合出不同的常量;
假设对X有K个截点,
我们生成K+1个新变量: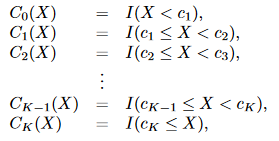
这些变量有时候也叫虚拟变量或哑变量,然后对这K+1个变量进行拟合,得到形如: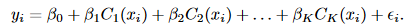
三,基底函数(basis functions)
前两种回归方式,都可以总结为是基底函数的特例。所谓的基底函数是不直接对X进行回归,而是用函数函数变化后的值进行回归,形如:
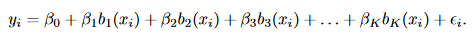
当 时,就变成了多项式回归;
当 时,就变成了分段回归;
四,回归样条(Regression Splines)
由基底函数可知,基函数可以是任意的组合形式,不过接下来我们介绍的一种基函数是结合了多项式和分段常值函数的”回归样条”.
什么是样条呢?
样条是一个函数,由多项式构造的分段函数,并且在分段节点处要具有高度平滑的特性,即在分段结点处连续且有连续的导数。
1,三次样条:
一个三次多项式分段回归如下,但是该回归并不满足”平滑的特性”,在结点处可能出现跳跃。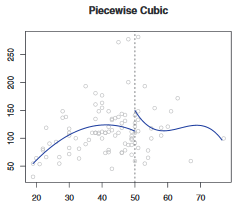
所以,我们要加两个限制条件,让其变成一个样条回归:
1)结点处连续;
2)结点处平滑;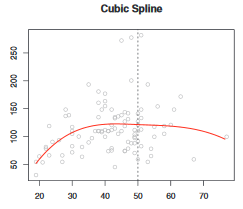
定义,K个节点下的三次样条回归模型: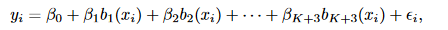
三次样条下,基函数也有非常多的选择,最直接的方法就是进行拟合
其中,是结点: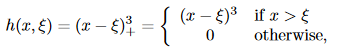
样条缺点是,有时候受异常点影响较大。需要加上额外的边界约束。
2,如何确定结点的个数与位置
一种方法是在变化相对稳定的区间设置尽量少的结点,在变化相对快速的地方设置尽量多的结点。尽量让每个结点区间内的变量趋于均匀分布。
另一种方法是设置自由度,根据算法自动跑出最优的结点位置。
自由度的个数可以结合交叉验证来验证。
3,与多项式回归的比较
由于样条有结点的帮助,所以在变动很大的数据背景下,仍然可以保证多项式的次数较小。而多项式回归则可能需要更多的次数 。一句话概括即是样条比多项式回归更灵活。
4,平滑样条曲线
假设我们样条函数为g(x),再求得该函数参数的同时,如何保证样条曲线的平滑性呢?
结合第四章所讲,在求解样条回归的结构风险最小化(RSS+惩罚项)时,把惩罚项设置为”平滑性”相关的表示,形如: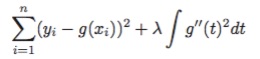
函数在某点处的一阶导数表示的该点曲线的斜率,二阶导数表示的就是斜率的变化率,即,惩罚项即表示为函数曲线在该点的平滑性。
但是,在一段区间内,曲线整体的平滑性要如何衡量呢?我们用到了。上式中的惩罚项表示为对区间t内,一阶导数累计的变化情况,因此可以用来衡量该段区间整体的平滑性了。
超参λ,则是用来衡量惩罚项的重要性占比的。一般用n折交叉验证或者留一交叉验证法来确定。
五,局部回归(Local Regression)
局部回归是另一种拟合非线性模型的方法。
为了实现局部回归,有许多重要步骤需要确定:
– 确定加权函数K
– 确定局部回归的模型:线性/二次/还是常数等,通常是简单模型
– 最重要的还是对“局部”的定义,如何确定点点近临范围“s”
范围s的值越小,每次拟合的数据区间越小,并且到下一个拟合点到距离也越小。我们可以用交叉验证的方法来确定s,或者人为设定一个值。
1)最简单的局部模型
局部平均(local average)模型是最简单的局部模型,形如: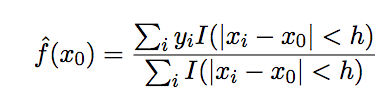
其缺点是,估计结果并非是连续的。
且与KNN的思想类似,是一种非参数方法。
2)Nadaraya-Watson 核估计(NW)
引用核估计方法,将local average模型进行改造,当K是连续时,f即为连续的。
其局部性参数h可以通过交叉验证的方式计算得到。
不过当x不是均匀分布的时候,该方法将产生偏倚。
3)lowess
前两种方法都属于非参数方法,下面介绍一种结合了非参和参数模型的方法:lowess或者又叫做loess,通过对局部进行线性拟合(非常数值拟合),来解决NW的缺点。
总结:
六,广义相加模型(Generalized Additive Models)
前面,我们已经介绍了一些方法,作为简单线性模型的扩展。这些方法可以归纳为广义相加模型(GAMs)的框架里,形如: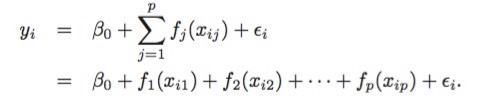
GAMs的优缺点:
– 可以引入非线性函数
– 非线性可能使得对Y预测的更准确
– 因为是”相加性的”,所以,线性模型的假设检验的方法仍然可以使用
– 因为是“相加性”假设,所以GAMs中可能会缺失重要的交互作用,只能通过手动添加交互项来弥补。
最后一个变量使用不多,因此我们将其删除,
titanic = titanic[,1:7]现在,我们回答问题:
幸存的旅客比例是多少?
简单的答案是
mean(titanic$Survived)
[1] 0.3838384可以在下面的列联表中找到
table(titanic$Survived)/nrow(titanic)
0 1
0.6161616 0.3838384或此处幸存者的38.38 %。也就是说,也可以通过不对任何解释变量进行逻辑回归来获得(换句话说,仅对常数进行回归)。回归给出了:
Coefficients:
(Intercept)
-0.4733
Degrees of Freedom: 890 Total (i.e. Null); 890 Residual
Null Deviance: 1187
Residual Deviance: 1187 AIC: 1189给出β0的值,并且由于生存概率为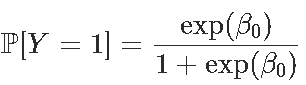
我们通过考虑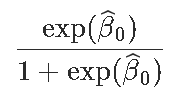
exp(-0.4733)/(1+exp(-0.4733))
[1] 0.3838355我们也可以使用predict函数
predict(glm(Survived~1, family=binomial,type="response")[1]
1
0.3838384此外,在概率回归中也适用,
reg=glm(Survived~1, family=binomial(link="probit"),data=titanic)
predict(reg,type="response")[1]
1
0.3838384幸存的头等舱乘客的比例是多少?
我们只看头等舱的人,
[1] 0.6296296约63%存活。我们可以进行逻辑回归
Coefficients:
(Intercept) Pclass2 Pclass3
0.5306 -0.6394 -1.6704
Degrees of Freedom: 890 Total (i.e. Null); 888 Residual
Null Deviance: 1187
Residual Deviance: 1083 AIC: 1089由于第1类是参考类,因此我们照旧考虑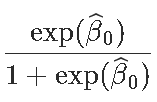
exp(0.5306)/(1+exp(0.5306))
[1] 0.629623predict预测:
predict(reg,newdata=data.frame(Pclass="1"),type="response")
1
0.6296296我们可以尝试概率回归,我们得到的结果是一样的,
predict(reg,newdata=data.frame(Pclass="1"),type="response")
1
0.6296296卡方独立性测试 :在生存与否之间的检验统计量是多少?
卡方检验的命令如下
chisq.test(table( Survived, Pclass))
Pearson's Chi-squared test
data: table( Survived, Pclass)
X-squared = 102.89, df = 2, p-value < 2.2e-16我们有一个列联表,如果变量是独立的,我们有![]() ,然后是统计量
,然后是统计量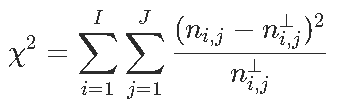 ,我们可以看到,对测试的贡献
,我们可以看到,对测试的贡献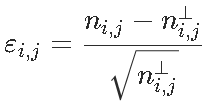
1 2 3
0 -4.601993 -1.537771 3.993703
1 5.830678 1.948340 -5.059981这给了我们很多信息:我们观察到两个正值,分别对应于“幸存”和“头等舱”与“无法幸存”和“三等舱”之间的强(正)关联,以及两个很强的负值,对应于“生存”和“第三等”之间的强烈负相关,以及“无法幸存”和“头等舱”。我们可以在下图上可视化这些值
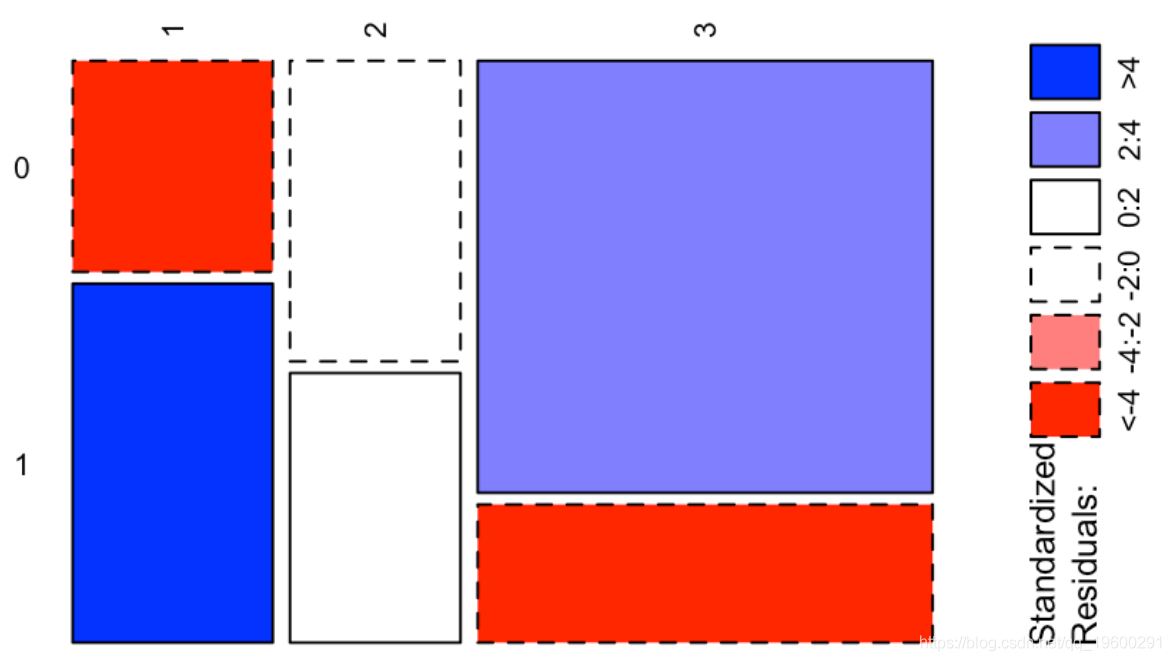
ass(table( Survived, Pclass), shade = TRUE, las=3)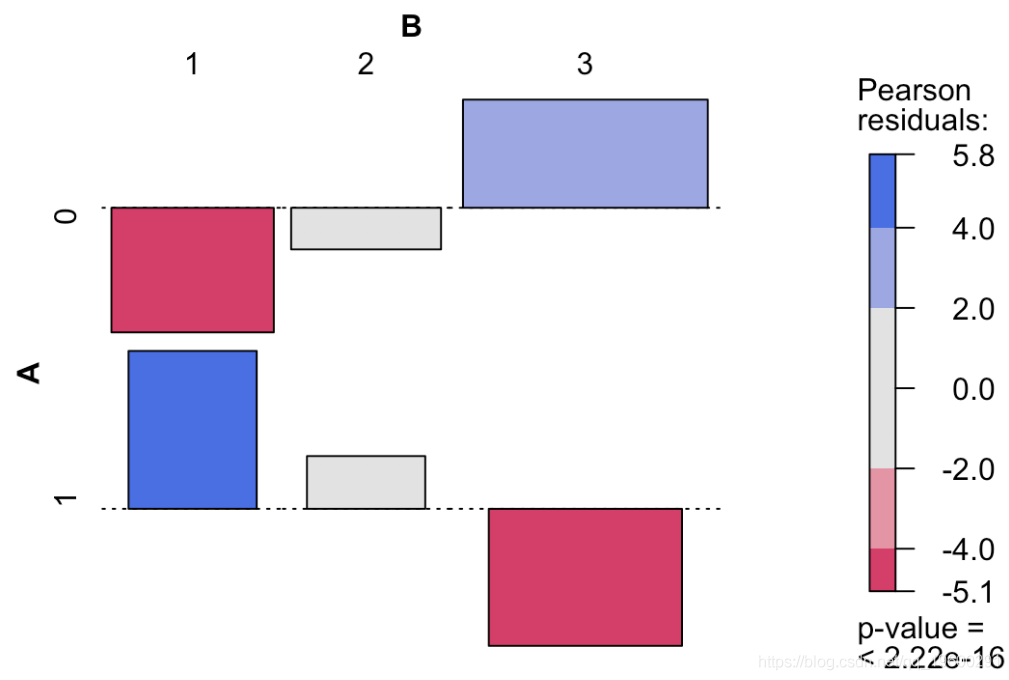
然后我们必须进行逻辑回归,并预测两名模拟乘客的生存概率
假设我们有两名乘客
newbase = data.frame(
Pclass = as.factor(c(1,3)),
Sex = as.factor(c("female","male")),
Age = c(17,20),
SibSp = c(1,0),
Parch = c(2,0),让我们对所有变量进行简单回归,
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 16.830381 607.655774 0.028 0.97790
Pclass2 -1.268362 0.298428 -4.250 2.14e-05 ***
Pclass3 -2.493756 0.296219 -8.419 < 2e-16 ***
Sexmale -2.641145 0.222801 -11.854 < 2e-16 ***
Age -0.043725 0.008294 -5.272 1.35e-07 ***
SibSp -0.355755 0.128529 -2.768 0.00564 **
Parch -0.044628 0.120705 -0.370 0.71159
EmbarkedC -12.260112 607.655693 -0.020 0.98390
EmbarkedQ -13.104581 607.655894 -0.022 0.98279
EmbarkedS -12.687791 607.655674 -0.021 0.98334
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 964.52 on 713 degrees of freedom
Residual deviance: 632.67 on 704 degrees of freedom
(177 observations deleted due to missingness)
AIC: 652.67
Number of Fisher Scoring iterations: 13两个变量并不重要。我们删除它们
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 4.334201 0.450700 9.617 < 2e-16 ***
Pclass2 -1.414360 0.284727 -4.967 6.78e-07 ***
Pclass3 -2.652618 0.285832 -9.280 < 2e-16 ***
Sexmale -2.627679 0.214771 -12.235 < 2e-16 ***
Age -0.044760 0.008225 -5.442 5.27e-08 ***
SibSp -0.380190 0.121516 -3.129 0.00176 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 964.52 on 713 degrees of freedom
Residual deviance: 636.56 on 708 degrees of freedom
(177 observations deleted due to missingness)
AIC: 648.56
Number of Fisher Scoring iterations: 5我们有年龄这样的连续变量时,我们可以进行多项式回归
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 3.0213 0.2903 10.408 < 2e-16 ***
Pclass2 -1.3603 0.2842 -4.786 1.70e-06 ***
Pclass3 -2.5569 0.2853 -8.962 < 2e-16 ***
Sexmale -2.6582 0.2176 -12.216 < 2e-16 ***
poly(Age, 3)1 -17.7668 3.2583 -5.453 4.96e-08 ***
poly(Age, 3)2 6.0044 3.0021 2.000 0.045491 *
poly(Age, 3)3 -5.9181 3.0992 -1.910 0.056188 .
SibSp -0.5041 0.1317 -3.828 0.000129 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 964.52 on 713 degrees of freedom
Residual deviance: 627.55 on 706 degrees of freedom
AIC: 643.55
Number of Fisher Scoring iterations: 5但是解释参数变得很复杂。我们注意到三阶项在这里很重要,因此我们将手动进行回归
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 5.616e+00 6.565e-01 8.554 < 2e-16 ***
Pclass2 -1.360e+00 2.842e-01 -4.786 1.7e-06 ***
Pclass3 -2.557e+00 2.853e-01 -8.962 < 2e-16 ***
Sexmale -2.658e+00 2.176e-01 -12.216 < 2e-16 ***
Age -1.905e-01 5.528e-02 -3.446 0.000569 ***
I(Age^2) 4.290e-03 1.854e-03 2.314 0.020669 *
I(Age^3) -3.520e-05 1.843e-05 -1.910 0.056188 .
SibSp -5.041e-01 1.317e-01 -3.828 0.000129 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 964.52 on 713 degrees of freedom
Residual deviance: 627.55 on 706 degrees of freedom
AIC: 643.55
Number of Fisher Scoring iterations: 5可以看到,p值是相同的。简而言之,将年龄转换为年龄的非线性函数是有意义的。可以可视化此函数
plot(xage,yage,xlab="Age",ylab="",type="l")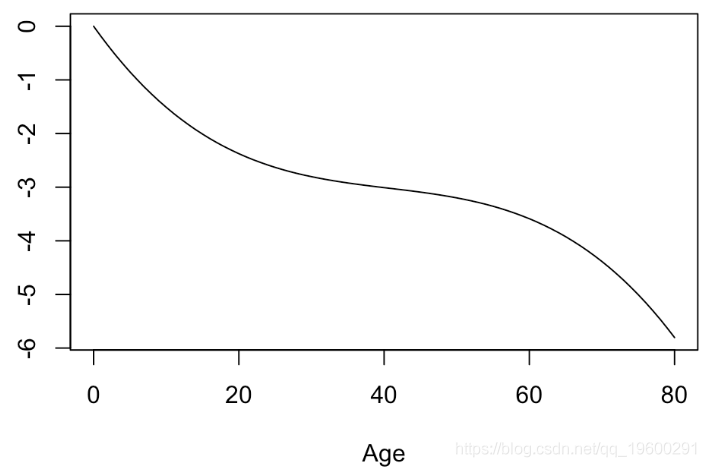
实际上,我们可以使用样条曲线。广义可加模型( gam )是完美的可视化工具
(Dispersion Parameter for binomial family taken to be 1)
Null Deviance: 964.516 on 713 degrees of freedom
Residual Deviance: 627.5525 on 706 degrees of freedom
AIC: 643.5525
177 observations deleted due to missingness
Number of Local Scoring Iterations: 4
Anova for Parametric Effects
Df Sum Sq Mean Sq F value Pr(>F)
Pclass 2 26.72 13.361 11.3500 1.407e-05 ***
Sex 1 131.57 131.573 111.7678 < 2.2e-16 ***
bs(Age) 3 22.76 7.588 6.4455 0.0002620 ***
SibSp 1 14.66 14.659 12.4525 0.0004445 ***
Residuals 706 831.10 1.177
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1我们可以看到年龄变量的变换,
并且我们发现变换接近于我们的3阶多项式。我们可以添加置信带,从而可以验证该函数不是真正的线性
我们现在有三个模型。最后给出了两个模拟乘客的预测,
predict(reg,newdata=newbase,type="response")
1 2
0.9605736 0.1368988
predict(reg3,newdata=newbase,type="response")
1 2
0.9497834 0.1218426
predict(regam,newdata=newbase,type="response")
1 2
0.9497834 0.1218426可以看到莱昂纳多·迪卡普里奥( Leonardo DiCaprio) 有大约12%的幸存机会(考虑到他的年龄,他有三等票,而且船上没有家人)。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!

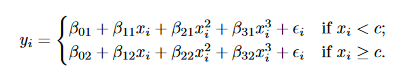
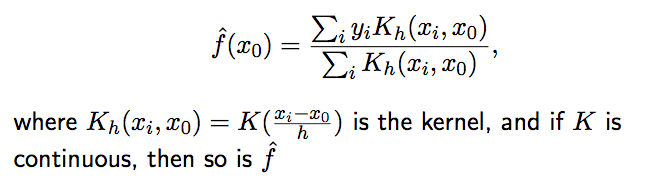
 Python梯度提升树GBT、随机森林、决策树对链家多城市二手房价格数据预测与区域差异可视化分析——基于数据爬取与特征工程优化|附代码数据
Python梯度提升树GBT、随机森林、决策树对链家多城市二手房价格数据预测与区域差异可视化分析——基于数据爬取与特征工程优化|附代码数据 Python农业气象预测:优化决策树、SHAP模型可解释性、滑动窗口时序分析及交叉验证
Python农业气象预测:优化决策树、SHAP模型可解释性、滑动窗口时序分析及交叉验证 视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析
视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析



