我们首先讨论多项式回归,进一步,我们会想到分段线性或分段多项式函数,可能还有附加的连续性约束,这些是样条曲线回归的基础。
在线性模型的文章中,我们已经了解了如何在给出协变量x的向量时构造线性模型。但更一般而言,我们可以考虑协变量的变换,来使用线性模型。
我们首先讨论多项式回归,进一步,我们会想到分段线性或分段多项式函数,可能还有附加的连续性约束,这些是样条曲线回归的基础。
多项式回归
谈论多项式回归时(在单变量情况下)
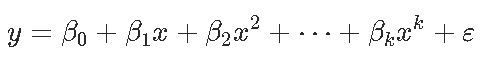
随着项数的增多,尽管可以对数据拟合越来越好,但随之而来的问题是过拟合。也就是说,在现在这个数据上拟合效果是很完美,然而一旦换个数据,很可能效果就很差。
除了上面这个原因,多项式还有其它问题,最常见的一个就是共线性。很容易理解,你把一个变量x变成一个平方后,平方值和原始值肯定有关联,原始值越大,平方值也越大。也就是说,自变量x和它的平方、立方等是存在共线性的。
当然还有其它原因,多项式回归是针对所有数据的,这叫做全局性。也就是说,所有我用来拟合的数据,都符合多项式的规律。如二次项,那就是符合抛物线的类似形状。然而,如果有的数据可能在小于某个值之前,是直线关系,到了这个值之后,开始成了二次项关系。这时候就不叫全局性了,因为所有数据不能用一种关系来表示,这就叫局部性。
这种数据,无论用直线和二次项,都没法很好地拟合所有数据。就像是你家的猫喜欢待在家里,不想出去,你家的狗总想出门。猫和狗如果非得作为一个总体,那就没法处理。那怎么办呢,很简单,把它们分开,狗带出去,猫留在家里。这也就是样条回归的基本思路,如果所有数据在某一点上有不同的变化趋势,怎么办,把数据分开,分别拟合。
我们使用
coef = leg.poly(n=4)
[[1]]
1
[[2]]
x
[[3]]
-0.5 + 1.5*x^2
[[4]]
-1.5*x + 2.5*x^3
[[5]]
0.375 - 3.75*x^2 + 4.375*x^4有许多正交多项式族(Jacobi多项式, Laguerre多项式, Hermite多项式等)。
在R中有用于多项式回归的标准多边形函数。
当使用poly时,我们使用矩阵的 QR分解。我们使用
poly - function (x, deg = 1) {
xbar = mean(x)
x = x - xbar
QR = qr(outer(x, 0:degree, "^"))
X = qr.qy(QR, diag(diag(QR$qr),这两个模型是等效的。
dist~speed+I(speed^2)+I(speed^3)
dist~poly(speed,3)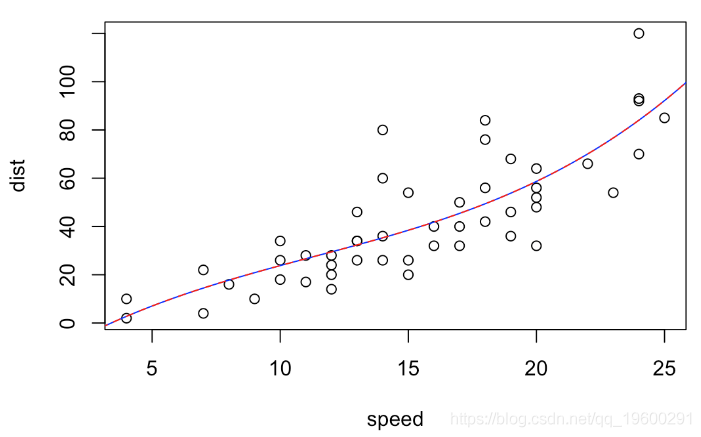
我们有完全相同的预测
v1[u==15]
121
38.43919
v2[u==15]
121
38.43919系数没有相同的解释,但是p值完全相同,两个模型以相同的置信度拒绝三次多项式,
summary(reg1)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -19.50505 28.40530 -0.687 0.496
speed 6.80111 6.80113 1.000 0.323
I(speed^2) -0.34966 0.49988 -0.699 0.488
I(speed^3) 0.01025 0.01130 0.907 0.369
Residual standard error: 15.2 on 46 degrees of freedom
Multiple R-squared: 0.6732, Adjusted R-squared: 0.6519
F-statistic: 31.58 on 3 and 46 DF, p-value: 3.074e-11
summary(reg2)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 42.98 2.15 19.988 < 2e-16 ***
poly(speed, 3)1 145.55 15.21 9.573 1.6e-12 ***
poly(speed, 3)2 23.00 15.21 1.512 0.137
poly(speed, 3)3 13.80 15.21 0.907 0.369
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 15.2 on 46 degrees of freedom
Multiple R-squared: 0.6732, Adjusted R-squared: 0.6519
F-statistic: 31.58 on 3 and 46 DF, p-value: 3.074e-11B样条曲线(B-spline curve)和GAM
样条曲线在回归模型中也很重要,尤其是当我们开始讨论 广义加性模型时。在单变量情况下,我通过引入(线性)样条曲线,
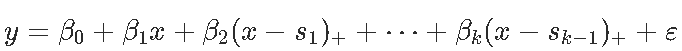
模型是连续的(连续函数的加权总和是连续的)。我们可以进一步
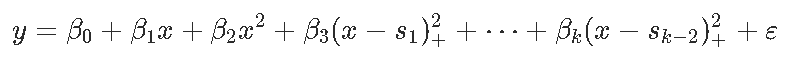
二次样条
用于三次样条。有趣的是,二次样条不仅是连续的,而且它们的一阶导数也是连续的(三次样条是连续的)。这些模型易于解释。例如,简单的模型
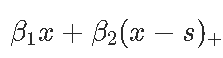
是以下连续的分段线性函数,在节点s处分段。
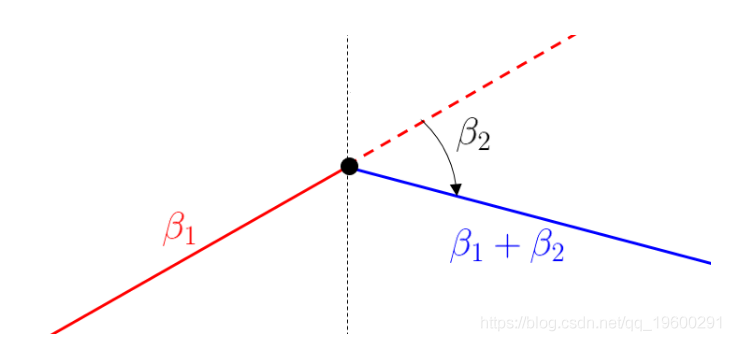
还应遵守以下解释:对于xx较小的值,线性增加,斜率\beta_1β1\;对于xx较大的值,线性减小,斜率\ beta_1 + \beta_2β1+β2。因此,\beta_2β2被解释为斜率的变化。
现在在R中使用bs函数(即标准B样条)并可视化
x = seq(5,25,by=.25)
B = bs(x,knots=c(10,20),Boundary.knots=c(5,55),degre=1)
matplot(x,B,type="l",lty=1,lwd=2,col=clr6)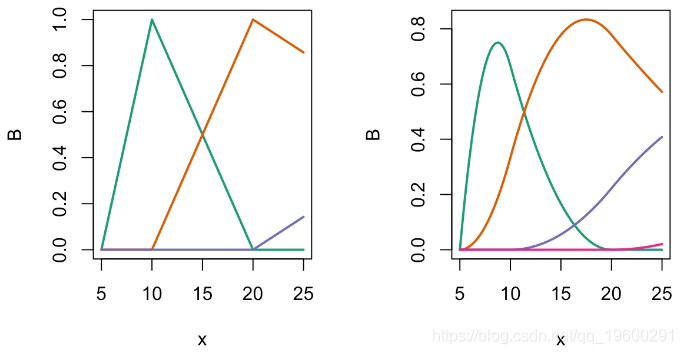
提到的函数如下
par(mfrow=c(1,2))
matplot(x,B,type="l",lty=1,lwd=2)
matplot(x,B,type="l",col=clr)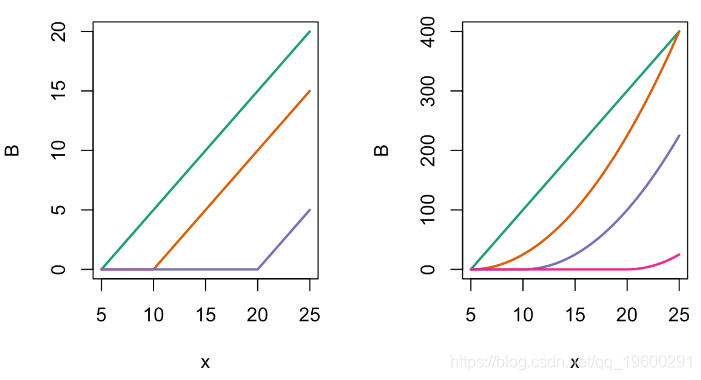
多项式回归中这两个模型表示方法是等效的。例如
dist~speed+pos(speed,10)+pos(speed,20
dist~bs(speed,degree=1,knots=c(10,20)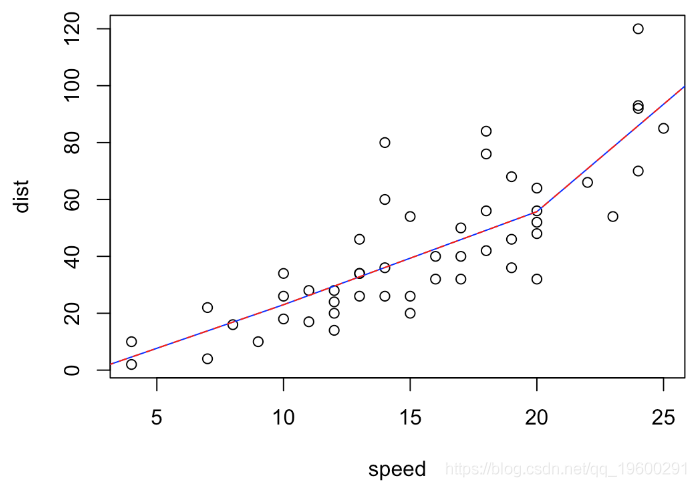
v1[u==15]
121
39.35747
v2[u==15]
121
39.35747这两个模型以及系数的解释是等效的:
summary(reg1)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -7.6305 16.2941 -0.468 0.6418
speed 3.0630 1.8238 1.679 0.0998 .
pos(speed, 10) 0.2087 2.2453 0.093 0.9263
pos(speed, 20) 4.2812 2.2843 1.874 0.0673 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 15 on 46 degrees of freedom
Multiple R-squared: 0.6821, Adjusted R-squared: 0.6613
F-statistic: 32.89 on 3 and 46 DF, p-value: 1.643e-11
summary(reg2)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.621 9.344 0.495 0.6233
bs(speed, degree = 1, knots = c(10, 20))1 18.378 10.943 1.679 0.0998 .
bs(speed, degree = 1, knots = c(10, 20))2 51.094 10.040 5.089 6.51e-06 ***
bs(speed, degree = 1, knots = c(10, 20))3 88.859 12.047 7.376 2.49e-09 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 15 on 46 degrees of freedom
Multiple R-squared: 0.6821, Adjusted R-squared: 0.6613
F-statistic: 32.89 on 3 and 46 DF, p-value: 1.643e-11在这里我们可以直接看到,第一个结点的斜率没有明显变化。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 Python梯度提升树、XGBoost、LASSO回归、决策树、SVM、随机森林预测中国A股上市公司数据研发操纵融合CEO特质与公司特征及SHAP可解释性研究|附代码数据
Python梯度提升树、XGBoost、LASSO回归、决策树、SVM、随机森林预测中国A股上市公司数据研发操纵融合CEO特质与公司特征及SHAP可解释性研究|附代码数据 Python谷歌商店Google Play APP评分预测:LASSO、多元线性回归、岭回归模型对比研究
Python谷歌商店Google Play APP评分预测:LASSO、多元线性回归、岭回归模型对比研究 Python、R语言南方电网、电力负荷数据多模型构建:分位数回归、GAM样条曲线、指数平滑和SARIMA与预测实践
Python、R语言南方电网、电力负荷数据多模型构建:分位数回归、GAM样条曲线、指数平滑和SARIMA与预测实践



