最近我们被客户要求撰写关于电力负荷预测的研究报告。根据我们对温度的预测，我们可以预测电力消耗。
绘制电力消耗序列图：
我们可以尝试一个非常简单的模型，其中日期Y_t的消耗量是时间，温度（多项式形式表示）以及工业生产指数IPI_t的函数。
可下载资源
plot(elect,type="l")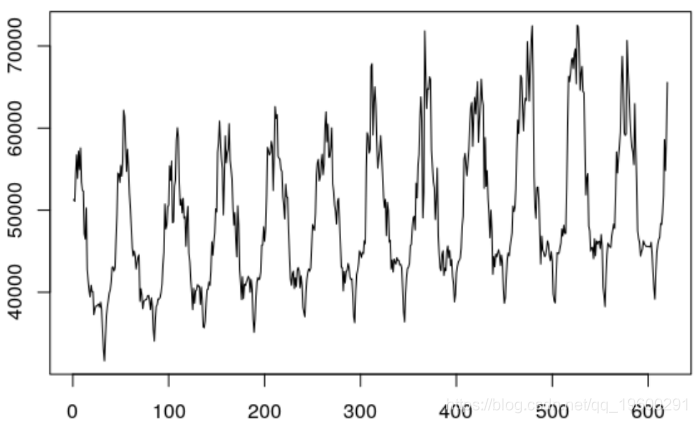
电力负荷预测是电网规划的基础，对电力电量平衡、主变定容选址、网架规划等环节具有重要的理论支撑作用。可以说，电力负荷预测贯穿于规划工作始终，预测水平的高低将直接影响电网规划质量的优劣。
负荷预测已经有不短的研究历史，涌现了大量比较成熟有效的预测方法。主要分为确定性预测方法和非确定性预测方法。确定性预测方法多把负荷用一个或一组方程来描述，负荷与影响其变化的因素之间有着明确的对应关系，包括回归分析法、时间序列法、负荷密度法、相关分析法、年最大负荷利用小时数法等。
而不确定性方法认为电力负荷的变化受众多模糊的、不确定的因素影响，它不可能用精确的显式数学方程来描述，包括专家经验法、神经网络法、模糊预测法、灰色模型法等。负荷预测的各种方法根据其自身的特点被应用于不同的场合。随着我国新型城镇化建设的推进，农村地区基本功能不断加强，人口迁移加剧、产业结构升级、生活方式及生活理念发生转变，负荷预测的复杂性进一步加深。前瞻性的开展农村电力负荷预测研究，可以满足地区城镇化发展对电网安全稳定、灵活调度的要求，适应长期可持续发展的需要，具有重大的现实意义。
lm(Load~1+Time+as.factor(Week)+poly(Temp,3)+Temp+IPI,data=elect )温度影响的多项式函数来自下图（去除线性趋势后的消耗序列）
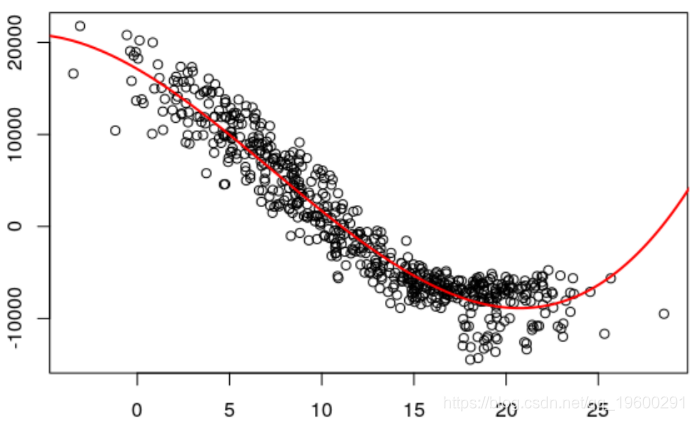
我们还可以假设自回归形式，其中Y_ {t} 是Y_ {t-1} 的函数
lm(Load~1+Load1+Time+as.factor(Week)+
poly(Temp,3)+Temp1+IPI,data=elect然后，我们可以尝试进行预测。第二个模型的问题是自回归部分。要预测Y_ {t + h} ，我们必须使用在t + h-1，Y ^ t + h − 1中所作的预测。
IPI = elect[futur,"IPI"])
for(t in 1:110){
base_prevision[t+1,"Load1"] = p}然后，我们可以预测 Y ^ t与观察值 Yt进行比较。
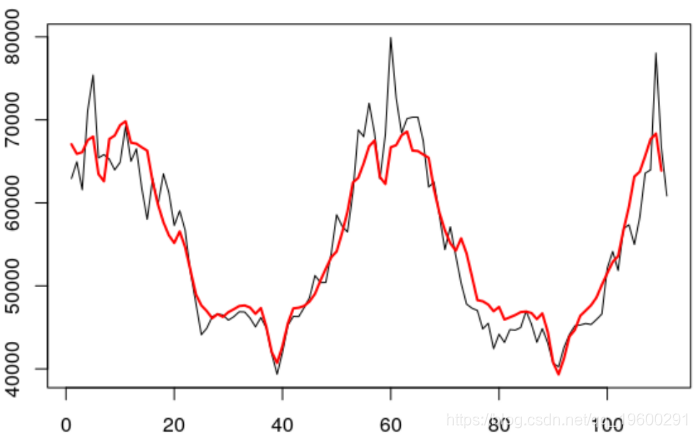
我们在夏季估计良好（我们预测了8月上半月的高峰），但我们低估了冬季的消耗量。
最后，我们可以忽略解释变量，而直接尝试建立时间序列模型。
plot(elect[passe,"Load"],type="l")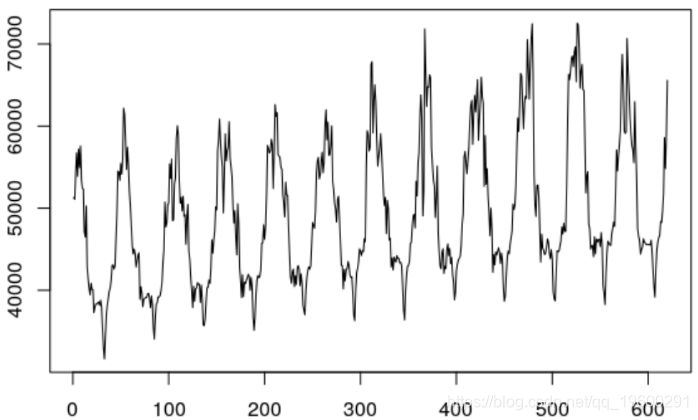
令人担忧的是该序列的异方差，其最小斜率低于最大斜率。
n=length(passe)="l")
m=aggregate(elect
by=list(as.f
points(sort((1
xM=((1:n)[vM])
regm=lm(m$x~xm,col="blue")
regM=lm(M$x~xM,col="blue")
abline(regm,lty=2)
abline(regM,lty=2)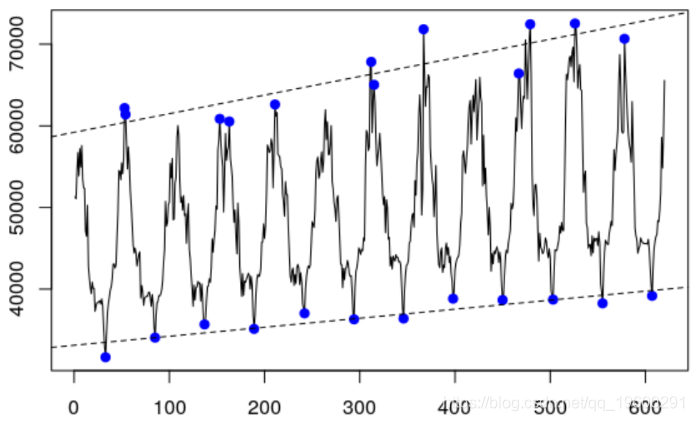
经典（简单）的解决方案是取对数
plot(elect
plot(z,type="l")
B = data.frame(z=z,t=1:length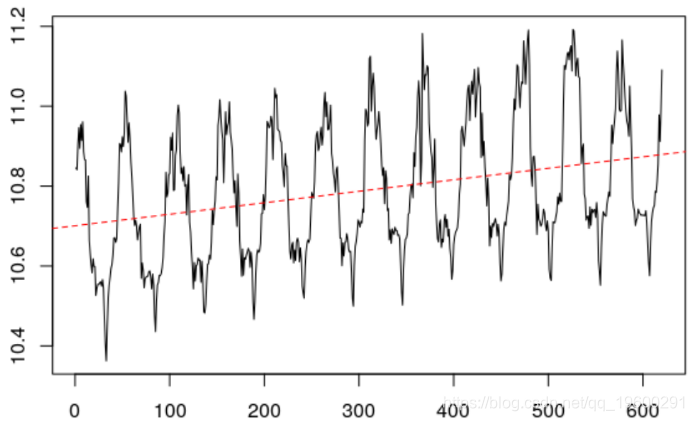
然后，我们必须消除线性趋势，以平稳序列
z = residuals(lm(z~t,data=B))
arima(Z,order = c(4,0,0),
seasonal = list(order = c(1 第一个模型是稳定的，没有单位根。我们可以尝试引入季节性单位根
arima(Z,order = c(0,0,0),
seasonal = list(order = c(0,1, 最后，最后一个要简单一些
arima(Z,order = c(1,0,0), seasonal = list(order = c(2,0,0)))然后，我们将所有预测存储在数据库中
然后将线性趋势添加到残差的预测中
reg = lm(z~t,data=B)
在这里，我们在 logY上建立了线性模型，即 logY〜N（μ，σ2），因此 E [Y] = exp（μ+σ2/ 2）
sqrt(predict(modelz1,n.ahead = 111)$se^2+sigma^2),
我们在这里假设两个模型（线性趋势和自回归模型的线性）的预测估计量是独立的，因此我们可以对方差项求和。另外，Y的预测是
exp(DOz$z1+1/2*DONNseu$seu1^2),
我们比较三个模型的预测（与观察值）
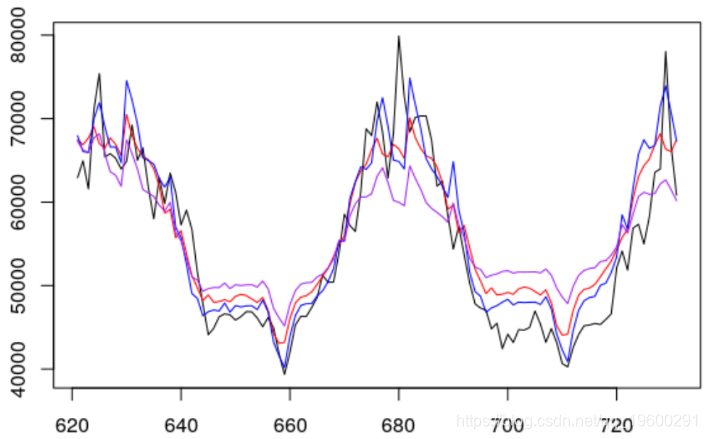
我们与之前的预测进行比较，
lines(futur,base_previ
col="orange")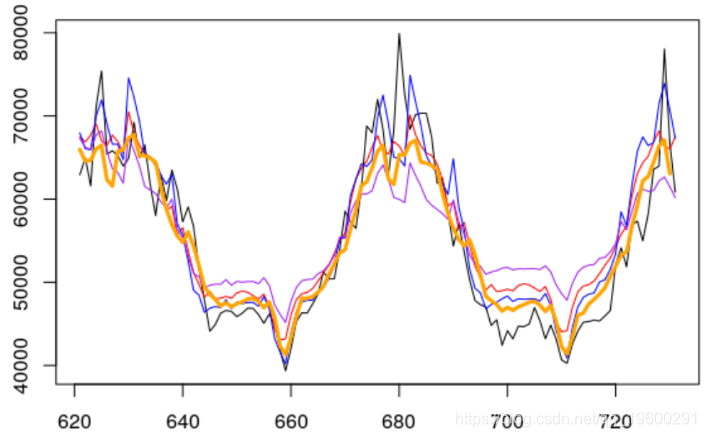
夏季预测会有所偏差，而冬季预测我们有所改善。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
MATLAB深度学习Transformer神经网络量化金融时间序列预测交易策略回测
Python注意力机制Attention下CNN-LSTM-ARIMA混合模型预测中国银行股票价格|附数据代码
【专题】2024年先进数据存力白皮书报告汇总PDF洞察（附原数据表）
Python用CNN – LSTM、ARIMA、Prophet股票价格预测的研究与分析|附数据代码
