利率衍生证券的定价依赖于描述基本过程的模型。这些利率模型取决于您必须通过将模型预测与市场上可用的现有数据进行匹配来确定的一个或多个参数。
在Hull-White模型中,有两个与短期利率过程相关的参数:均值回归和波动率。
对于Hull-White模型,关于均值回归(α)和波动率(σ)最小化是二维的。也就是说,校准Hull-White模型可最大程度地减少模型的预测价格与观察到的市场价格之间的差异。
可下载资源
Hull-White校准示例
使用市场数据来识别为构建工具定价的Hull-White树所需的隐含波动率(σ)和均值回归(α)系数,必须对市场数据进行插值。
衍生品的价格等于未来收益的折现在风险中性测度下的期望,权益相关的衍生品定价相对较简单,一般来说是假定股票价格服从几何布朗运动,如果需要复杂一点的模型还可以加上种种调整,比如跳跃项等。而利率的随机过程较为复杂,利率衍生品也几乎是最复杂的衍生品,到目前为止,比较流行的利率模型主要有以下几种。
1. Hull-White模型
该模型是最基础的一种利率模型,思路与实现都较为简单。容易看出该模型有很好的均值回复特性,当r(t)大于或小于a/b时,漂移项会使向反方向运动,从而使其在a/b附近波动。
如果将模型变得稍微复杂一点,便可以允许参数随时间变化,但要求其是关于时间的确定函数,那么Vasicek模型就变为了Hull-White模型。
在此利率过程下,许多衍生品的价格便可以通过折现求期望得到了。某利率衍生品在T时刻的收益为X,如果X的形式很简单,那么便可以用积分的方式求出该资产的价格,否则,便需要使用一些数值方法来计算,比较常用的便是二叉树、有限差分、蒙特卡洛等。
2. CIR模型
上面的Vasicek模型有一个缺点,那就是利率可能为负值,这与我们的常识相违背,至少在中国还未出现过负利率的情况。为了对这种情况进行改进,CIR模型应运而生。
3. HJM模型
HJM模型是由Heath, Jarrow, Morton于1992年提出的一种新的利率建模方法,与其说它是一种模型,不如说它是一种框架,该框架非常重要的一个作用就是为利率期限结构提供了无套利约束。
HJM模型与上面的两种模型的不同点在于其建模的对象不是瞬时利率,而是远期瞬时利率。何为远期瞬时利率?正如瞬时利率是\delta趋于0时从t时刻到t+\delta时刻的利率,为t时刻在趋于0时从T时刻到T+\delta时刻的远期利率。
HJM 最大的优点在于其显式保证了无套利条件,只要满足上述等式即可。前面几种模型本质上是HJM模型的一种特殊情况,很容易验证Vasicek,Hull-White,Ho-Lee,CIR模型均满足HJM模型的无套利条件,其分别为不同函数得到的结果。
4. 远期LIBOR模型
为了克服HJM模型的缺陷,为cap期权提供优雅的解析解,在众多学者的努力下,远期LIBOR模型诞生,该模型建模的对象是远期简单利率。
考虑具有以下参数的上限:
Strike = 0.0690;
Reset = 4;
Principal = 1000; datestr(capletDates')ans =
21-Mar-2008
21-Jun-2008
21-Sep-2008
21-Dec-2008
21-Mar-2009
21-Jun-2009
21-Sep-2009
21-Dec-2009
21-Mar-2010
21-Jun-2010
21-Sep-2010
21-Dec-2010
21-Mar-2011在最佳情况下,查找带有Strike =的 市场波动率 0.0690,以及列出的到期日,但找到这些确切数据的可能性很小。结果,使用市场上可用的数据并进行插值。
根据市场数据,您可以获得不同日期和行使价的上限信息。
| 到期 | 协议1 = 0.0590 | 协议2 = 0.0790 |
|---|---|---|
| 2008年3月21日 | 0.1533 | 0. 1526 |
| 2008年6月21日 | 0.1731 | 0. 1730 |
| 2008年9月21日 | 0. 1727 | 0. 1726 |
| 2008年12月21日 | 0. 1752 | 0. 1747 |
| 2009年3月21日 | 0. 1809 | 0. 1808 |
| 2009年6月21日 | 0. 1809 | 0. 1792 |
| 2009年9月21日 | 0. 1805 | 0. 1797 |
| 2009年12月21日 | 0.1802 | 0. 1794 |
| 2010年3月21日 | 0.1802 | 0. 1733 |
| 2010年6月21日 | 0. 1757 | 0. 1751 |
| 2010年9月21日 | 0. 1755 | 0. 1750 |
| 2010年12月21日 | 0. 1755 | 0. 1745 |
| 2011年3月21日 | 0. 1726 | 0. 1719 |
要求日期,协议价和实际波动分为三个变量: MarketStrike, MarketMat,和 MarketVol。
MarketStrike = [0.0590; 0.0790];
MarketMat = {'21-Mar-2008';
'21-Jun-2008';
'21-Sep-2008';
MarketVol = [0.1533 0.1731 0.1727 0.1752 0.1809 0.1800 0.1805 0.1802 0.1735 0.1757 ... 使用此数据完成输入参数 RateSpec:
RateSpec =
FinObj: 'RateSpec'
Compounding: 4
Disc: [14x1 double]
Rates: [14x1 double]
EndTimes: [14x1 double]
StartTimes: [14x1 double]
EndDates: [14x1 double]
StartDates: 733428
ValuationDate: 733428
Basis: 0
EndMonthRule: 1调用校准例程以找到波动率参数Alpha和Sigma的值
根据市场数据计算的值 Alpha ,Sigma 。例如,您可以将目标函数的公差定义为 100*eps :
Local minimum possible.
> In hwcalbycapfloor at 93
In hwcalbycap at 75
Alpha =
1.0000e-06
Sigma =
0.0127先前的警告表明转换不是最佳的。使用的搜索算法未找到符合所有约束的解决方案。要辨别该解决方案是否可接受,请通过为以下项指定第三个输出(OptimOut)来查看 优化结果:
hwcalbycap(RateSpec, MarketStrike, MarketMat,...
结构的 OptimOut.residual 字段 OptimOut是优化残差。此值包含Black caplet和优化过程中计算出的值之间的差异。您可以使用该 OptimOut.residual 值计算与Black Caplet价格相比的百分比差异(误差),然后确定残差是否可以接受,决定是否接受以单一数值参数化的市场 Alpha 和 Sigma。
使用市场数据和Black模型获取价格
Black -76模型被认为是世界范围内广泛接受的互换期权定价模型,互换期权计算公式看起来和期权价格公式一 样,这表示在使用Black模型对互换期权进行定价时,可以用和定价期权时同样的方法进行计算.为了使Black模型生效,只需输入由市场决定的隐含波动率即可。
为了确定优化的有效性,请使用Black公式和市场数据计算参考值。请注意,您必须首先对市场数据进行插值以获得用于计算的数据量:
FlatVol = interp2(Mats, Strikes, MarketVol, datenum(Maturity), 使用Black模型计算价格:
capbybike, Settle, Maturity, FlatVol,...
Caplets = 0.3210 1.6355比较优化值和Black值并以图形方式显示
在计算了参考值之后,请通过分析和图形方式比较这些值,以确定是否计算出的单个值 Alpha 并 Sigma 提供适当的近似值:
plot(MarketMatNum(2:end), Caplets, 'or', MarketMatNum(2:end), Oylabel('Caplet Price');tset(gcf, 'NumberT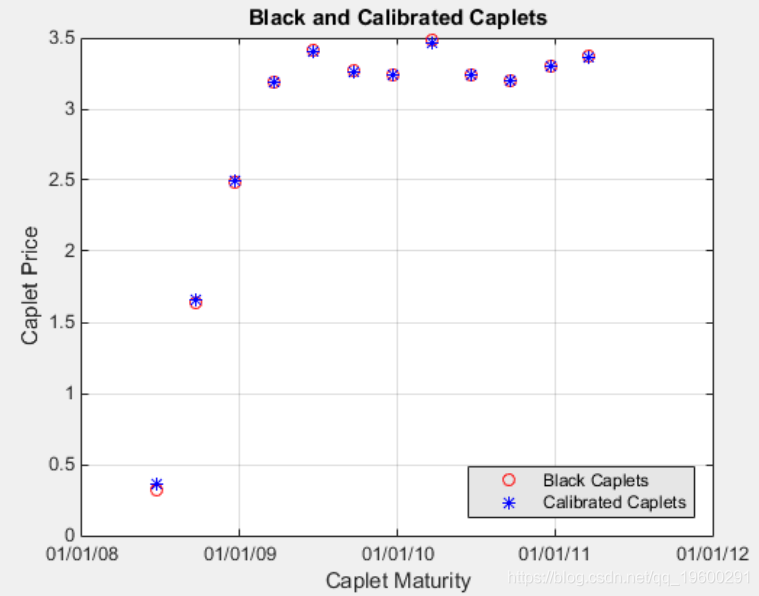
使用Black,HW分析和HW树模型比较上限价格
使用Black模型,Hull-White分析模型和Hull-White树模型比较相应上限价格。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 MATLAB用CNN-LSTM神经网络的语音情感分类深度学习研究
MATLAB用CNN-LSTM神经网络的语音情感分类深度学习研究 MATLAB模糊C均值聚类FCM改进的推荐系统协同过滤算法分析MovieLens电影数据集
MATLAB模糊C均值聚类FCM改进的推荐系统协同过滤算法分析MovieLens电影数据集 Python、MATLAB股票投资:ARIMA模型最优的选股方案和投资组合方案与预测
Python、MATLAB股票投资:ARIMA模型最优的选股方案和投资组合方案与预测 MATLAB数据挖掘用改进的K-Means(K-均值)聚类算法分析高校学生的期末考试成绩数据
MATLAB数据挖掘用改进的K-Means(K-均值)聚类算法分析高校学生的期末考试成绩数据



