维度规约（降维）算法在WEKA中应用

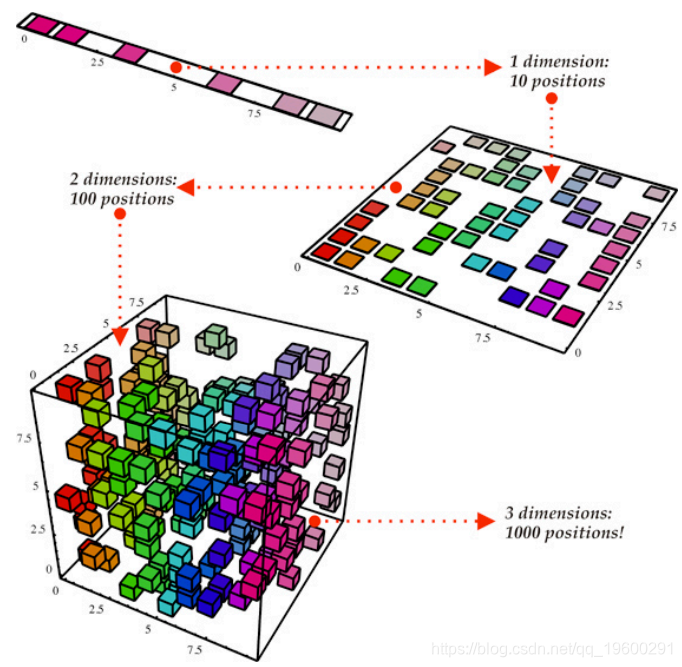
维度的诅咒是一种现象，即数据集维度的增加导致产生该数据集的代表性样本所需的指数级更多的数据。 为了对抗维度的诅咒，已经开发了许多线性和非线性降维技术。这些技术旨在通过特征选择或特征提取来减少数据集中维度（变量）的数量， 而不会显着丢失信息。特征提取是将原始数据集转换为维数较少的数据集的过程。两个众所周知的，密切相关的特征提取技术是主成分分析（PCA）和自组织映射（SOM）。人们可以把降维作为一个渡槽系统来理解数据的河流。​

主成分分析（PCA）

主成分分析（PCA）是一种统计算法，用于将一组可能相关的变量转换为一组称为主成分的变量的不相关线性重组。简而言之，主要组成部分，ÿ，是我们数据集中变量的线性组合， X，那里的权重， ËĴŤ是从我们的数据集的协方差或相关矩阵 的特征向量导出的。

第一个主要成分是使数据点距离的平方和最小的直线。它是单行数据集的最小二乘逼近。因此，第一个主要组成部分解释了数据集的最高变异量。然后从数据集中提取残差并计算下一个主成分。如此，每个连续的部件解释较少的方差，从而从中减少了变量的个数 X， 米，主要组件的数量， ķ。在使用PCA时存在一些挑战。从而从中减少了变量的个数 X， 米，主要组件的数量， ķ。在使用PCA时存在一些挑战。首先，该算法对数据集中变量的大小敏感，因此建议采用平均中心，而采用相关矩阵X因为它是正常化的。 PCA的另一个挑战是它本质上是线性的。PCA的非线性适应包括非线性PCA和内核PCA。

自组织映射（SOM）

自组织映射（SOMs）最初是由Kohonen在20世纪90年代中期发明的，有时也被称为Kohonen Networks。SOM是一种多维缩放技术，它构建了一些底层数据集的概率密度函数的近似值，X，这也保留了该数据集的拓扑结构。

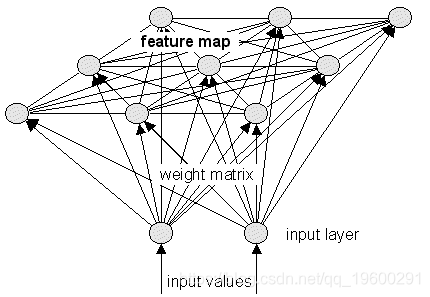
这是通过映射输入向量来完成的， X一世在数据集中， X，权重矢量， w ^Ĵ，特征地图中的（神经元） w ^。保留拓扑结构简单地意味着如果两个输入向量靠近在一起X，那些输入向量映射到的神经元 w ^也将紧密结合在一起。这是SOM的特点。​

如果SOM中的神经元数量少于数据集中的模式数量，那么我们将降低数据集的维数…而不是输入或权向量的维数。因此，由SOM执行的维度降低的类型与由PCA执行的降维类型不同，并且SOM实际上更类似于诸如K均值聚类的 聚类算法。

然而，SOM和聚类的区别在于数据集的聚类将（一般来说）保留数据集的概率密度函数，而不是数据集的拓扑结构。这使SOM特别有用于可视化。通过定义一个将给定权向量转化为颜色的次函数，我们能够将底层数据集的拓扑结构，相似性和概率密度函数可视化为一个较低的维数（通常是两维因为网格）。

PCA的应用

“Weka是数据挖掘任务的机器学习算法集合，它可以直接应用于数据集，也可以从您自己的Java代码中调用.Weka包含数据预处理，分类，回归，聚类，关联规则，可视化，也非常适合开发新的机器学习方案。“ [ 来源 ]

WEKA中的一个特性是选择属性和降维的工具。其中一个支持的算法是主成分分析。本示例将PCA应用于包含12个相关技术指标的.CSV文件。冗余是导致模型（特别是机器学习模型）过度拟合的数据质量之一。​

相关矩阵技术指标

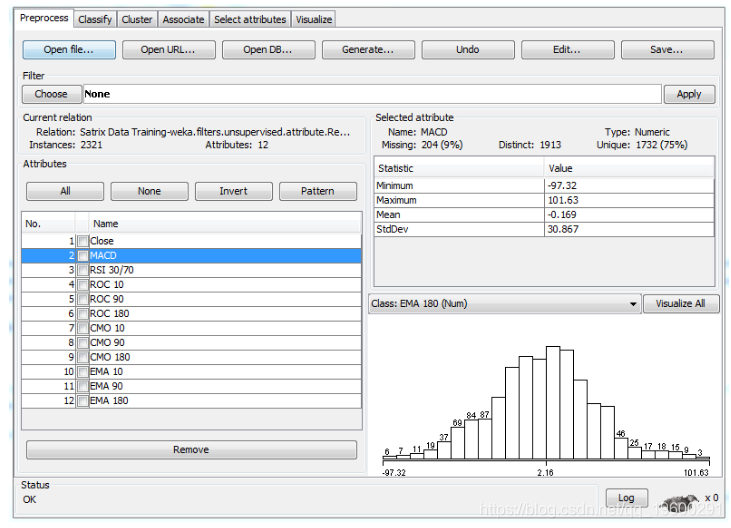
如果我们把它加载到WEKA中，我们将看到数据集的一些基本的描述性统计，包括每个变量（技术指标）的直方图，以及它们的最小值，最大值，平均样本统计量和标准差样本统计量。​

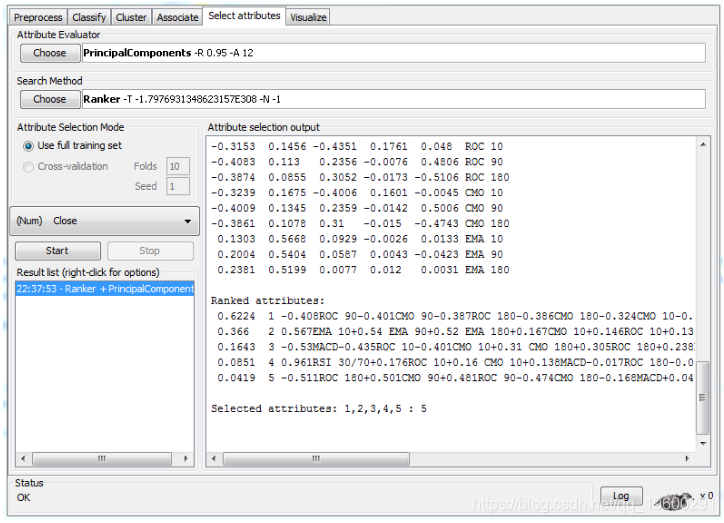
在选择属性选项卡中，选择主要组件属性评估器，WEKA将自动选择排序器搜索方法。​

点击开始后，WEKA提取前五个主要组件。可以看出，前三个主成分与收盘价的相关系数分别为0.6224,0.3660和0.1643。知道PCA，这三个组成部分是不相关的，理论上至少应包含有关指数运动的不同信息。

​非常感谢您阅读本文，有任何问题请在下面留言！

1

1

---

关于作者

Kaizong Ye是拓端研究室（TRL）的研究员。