神经网络是一种基于现有数据创建预测的计算系统。
如何构建神经网络?
可下载资源
神经网络包括:
- 输入层:根据现有数据获取输入的层
- 隐藏层:使用反向传播优化输入变量权重的层,以提高模型的预测能力
- 输出层:基于输入和隐藏层的数据输出预测
用神经网络解决分类问题
在这个特定的例子中,我们的目标是开发一个神经网络来确定股票是否支付股息。
因此,我们使用神经网络来解决分类问题。通过分类,我们指的是按类别对数据进行分类的分类。例如,水果可分为苹果,香蕉,橙等。
我们的自变量如下:
- fcfps:每股自由现金流量
- income_growth:过去一年的盈利增长(%)
- de:债务与权益比率
- mcap:股票的市值
- current_ratio:流动比率(或流动资产/流动负债)
我们首先设置目录并将数据加载到R环境中:
setwd("你的工作文件目录")
attach(mydata)形成神经网络时最重要的过程之一是数据标准化。这涉及将数据调整到一致的比例,以便准确地比较预测值和实际值。
无法对数据进行标准化通常会导致所有观察结果中的预测值保持不变,而与输入值无关。
我们在下面实现了这两种技术,但选择使用max-min标准化技术。
缩放标准化
scaleddata <-scale(mydata)
最大最小标准化
对于此方法,我们调用以下函数来标准化我们的数据:
normalize < - function(x){
return((x - min(x))/(max(x) - min(x)))
} 然后,我们使用lapply在我们现有的数据上运行该函数(我们将数据集称为加载到R中的数据集为mydata):
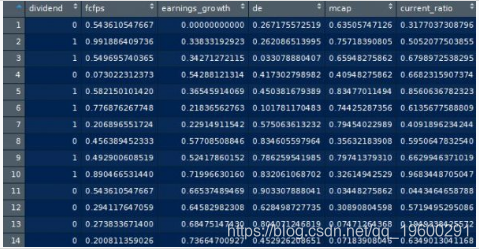
我们现在已经标准化了我们的新数据集并将其保存到名为maxmindf的数据框中:
我们的训练数据(训练集)基于80%的观测值。测试数据(测试集)基于剩余的20%的观察结果。
#训练和测试数据
trainset <- maxmindf[1:160, ]
testset <- maxmindf[161:200, ]用神经网络训练模型
我们现在将神经网络库加载到R.
使用神经网络将依赖的“红利”变量“回归” 到其他自变量
- 根据hidden =(2,1)公式将隐藏层数设置为(2,1)
- 给定自变量对因变量(被除数)的影响假设是非线性的,linear.output变量设置为FALSE
- 阈值设置为0.01,这意味着如果迭代期间的误差变化小于1%,则模型不会进行进一步的优化
确定神经网络中隐藏层的数量并不是一门精确的科学。事实上,有些情况下,没有任何隐藏层,准确度可能会更高。因此,反复试验在这一过程中起着重要作用。
一种可能性是比较预测的准确性如何随着我们修改隐藏层的数量而改变。例如,对于该示例,使用(2,1)参数配置最终产生92.5%的分类准确度。
nn $ result .matrix
plot(nn)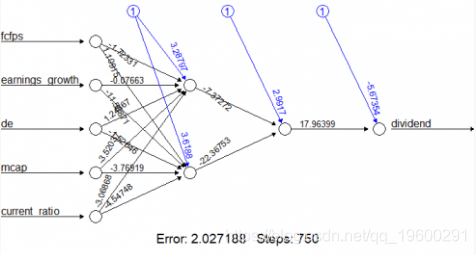
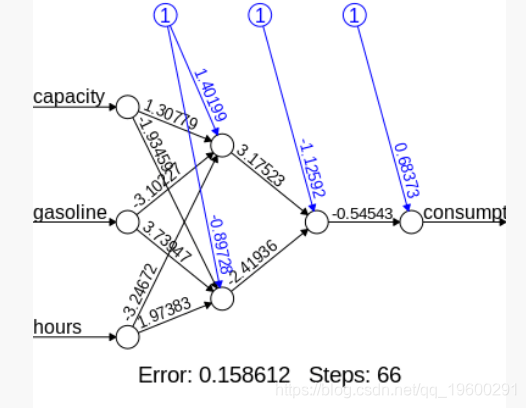
我们的神经网络看起来像这样:
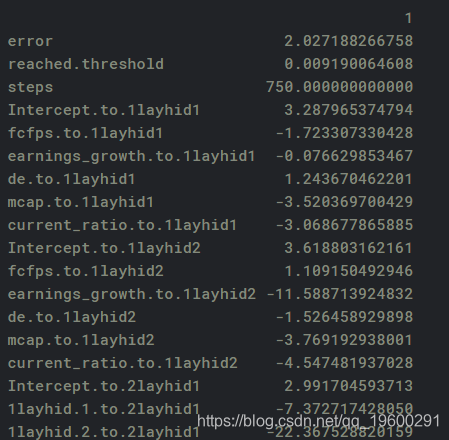
我们现在生成神经网络模型的误差,以及输入,隐藏层和输出之间的权重:
随时关注您喜欢的主题
测试模型的准确性
如前所述,我们的神经网络是使用训练数据创建的。然后,我们将其与测试数据进行比较,以评估神经网络预测的准确性。
temp_test < - subset(testset,select = c(“fcfps”,“earnings_growth”,“de”,“mcap”,“current_ratio”))
head(temp_test)
nn.results < - compute(nn, temp_test)
结果< - data.frame(actual = testset $ dividend,prediction = nn.results $ net.result)将预测结果与实际结果进行比较:
0.999985252611
混淆矩阵
然后,我们使用sapply对结果进行舍入,并创建一个混淆矩阵来比较真/假阳性和阴性的数量:
table(actual,prediction)
prediction
actual 0 1
0 17 0
1 3 20
最终,我们在确定股票是否支付股息时产生92.5%(37/40)的准确率。
混淆矩阵用于确定由我们的预测生成的真实和错误的数量。该模型生成17个真阴性(0),20个真阳性(1),而有3个假阴性。
使用神经网络解决回归问题
在这个例子中,我们希望分析解释变量容量,汽油和小时数对因变量消费的影响。
数据标准化
同样,我们将数据标准化并分为训练和测试数据:
#最大最小标准化
normalize < - function(x){
}
#训练和测试数据
trainset < - maxmindf [1:32,]
testset < - maxmindf [33:40,] 神经网络输出
然后我们运行我们的神经网络并生成我们的参数:
Intercept.to.1layhid1 1.401987575173
capacity.to.1layhid1 1.307794013481
gasoline.to.1layhid1 -3.102267882386
hours.to.1layhid1 -3.246720660493
Intercept.to.1layhid2 -0.897276576566
capacity.to.1layhid2 -1.934594889387
gasoline.to。 1layhid2 3.739470402932
hours.to.1layhid2 1.973830465259
Intercept.to.2layhid1 -1.125920206855
1layhid.1.to.2layhid1 3.175227041522
1layhid.2.to.2layhid1 -2.419360506652
Intercept.to.consumption 0.683726702522
2layhid.1.to.consumption -0.545431580477 生成神经网络
以下是我们的神经网络的可视化结果:
模型验证
然后,我们通过比较从神经网络产生的估计汽油消费与测试输出中报告的实际消费来验证(或测试我们模型的准确性):
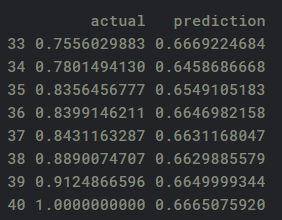
准确性
在下面的代码中,我们然后将数据转换回其原始格式,在平均绝对偏差的基础上产生90%的准确度(即估计和实际汽油消费之间的平均偏差平均为10%)。请注意,我们还将数据转换回标准值,因为它们之前使用max-min标准化方法进行了调整:
predicted=results$prediction * abs(diff(range(consumption))) + min(consumption)
accuracy
可以看到我们使用(2,1)隐藏配置获得90%的准确率。这非常好,特别是考虑到我们的因变量是区间格式。但是,让我们看看我们是否可以让它更高!
如果我们现在在神经网络中使用(5,2)隐藏层节点配置会发生什么?这是生成的输出:
accuracy=1-abs(mean(deviation))
accuracy
[1] 0.9577401232我们看到我们的准确率现已增加到近96%,表明修改隐藏节点的数量已经提高了我们的模型!
数据样例:
| dividend | fcfps | earnings_growth | de | mcap | current_ratio |
|---|---|---|---|---|---|
| 0 | 2.75 | -19.25 | 1.11 | 545 | 0.924055665 |
| 1 | 4.96 | 0.83 | 1.09 | 630 | 1.46857223 |
| 1 | 2.78 | 1.09 | 0.19 | 562 | 1.975875106 |
| 0 | 0.43 | 12.97 | 1.7 | 388 | 1.941997716 |
| 1 | 2.94 | 2.44 | 1.83 | 684 | 2.487466999 |
| 1 | 3.9 | -6.29 | 0.46 | 621 | 1.783252522 |
| 1 | 1.09 | -5.65 | 2.32 | 656 | 1.189733084 |
| 0 | 2.32 | 15 | 3.34 | 351 | 1.729519398 |
| 1 | 2.5 | 11.86 | 3.15 | 658 | 1.926789466 |
| 1 | 4.46 | 23.48 | 3.33 | 330 | 2.813534511 |
| 0 | 2.75 | 20.24 | 3.61 | 127 | 0.130219035 |
| 0 | 1.52 | 19.08 | 2.53 | 318 | 1.662392098 |
| 0 | 1.42 | 21.39 | 3.22 | 155 | 0.567528706 |
| 0 | 1.06 | 24.47 | 1.84 | 153 | 1.845205694 |
| 1 | 3.16 | 24.35 | 2.82 | 411 | 1.413293089 |
| 1 | 2.68 | 22.39 | 3.57 | 517 | 2.1049045 |
| 1 | 1.98 | 22.62 | 2.38 | 750 | 1.8154703 |
| 0 | 1.83 | 28.75 | 1.42 | 292 | 1.759152486 |
| 1 | 4.37 | 33.99 | 2.1 | 322 | 1.834702324 |


 CrewAI与GPT融合多智能体MAS与实时数据预测2026T20世界杯胜者|附代码数据
CrewAI与GPT融合多智能体MAS与实时数据预测2026T20世界杯胜者|附代码数据 llama的Qwen3.5大模型单GPU高效部署与股票筛选应用|附代码教程
llama的Qwen3.5大模型单GPU高效部署与股票筛选应用|附代码教程 R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据
R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据 R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据
R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据



