让我们看一个经济学的例子：假设你想购买一定数量q的特定产品。
如果单价是p，那么你会支付总金额y。这是一个线性关系的典型例子。总价格和数量成正比。
可下载资源
如下所示：
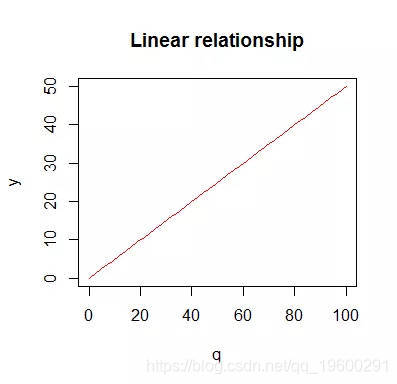
如果数据比简单的直线更为复杂，我们也可以用线性模型来你和非线性数据。一个简单的方法就是将每一个特征的幂次方添加为一个新的特征，然后在这个拓展的特征集上进行线性拟合，这种方法成为多项式回归。
回归分析的目标是根据自变量（或自变量向量）x 的值来模拟因变量 y 的期望值。在简单的线性回归中，使用模型
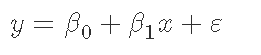
其中ε是未观察到的随机误差，其以标量 x 为条件，均值为零。在该模型中，对于 x 值的每个单位增加，y 的条件期望增加 β1β1个单位。
在许多情况下，这种线性关系可能不成立。例如，如果我们根据合成发生的温度对化学合成的产率进行建模，我们可以发现通过增加每单位温度增加的量来提高产率。在这种情况下，我们可能会提出如下所示的二次模型：
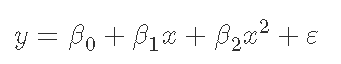
通常，我们可以将 y 的期望值建模为 n 次多项式，得到一般多项式回归模型：
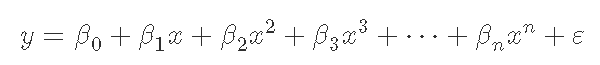
为了方便，这些模型从估计的角度来看都是线性的，因为回归函数就未知参数β0β0、β1β1等而言是线性的。因此，对于最小二乘分析，多项式回归的计算和推理问题可以使用多元回归技术完全解决，这是通过将 xx、x2x2 等视为多元回归模型中的独特自变量来完成的。
但购买和出售，我们可能要考虑一些其他相关信息，就像如果购买大量商品时我们很可能要求获得折扣，或出售更重要的商品时我们可能会提高价格。
最后可能是这样的情况，总成本不再是数量的线性函数：
通过多项式回归，我们可以将n阶模型拟合到数据上，并尝试对非线性关系进行建模。
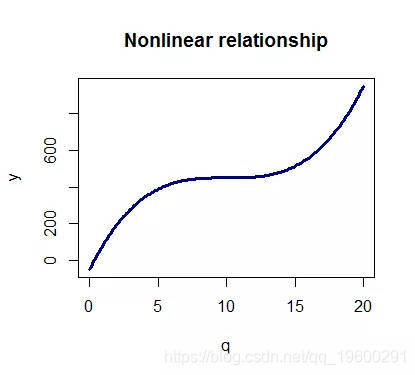
如何拟合多项式回归
这是我们模拟观测数据的图。模拟的数据点是蓝色的点，而红色的线是信号（信号是一个技术术语，通常用于表示我们感兴趣检测的总体趋势）。
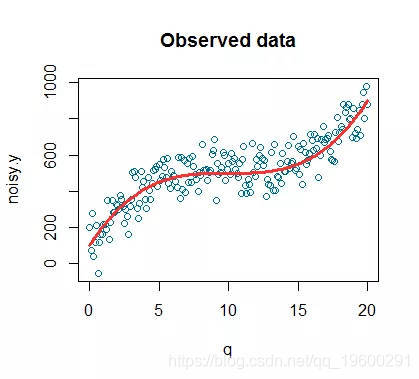
让我们用R来拟合。当拟合多项式时，您可以使用
lm（noisy.y~poly（q，3））
通过使用confint()函数，我们可以获得我们模型参数的置信区间。
模型参数的置信区间：
confint（model，level = 0.95）拟合vs残差图
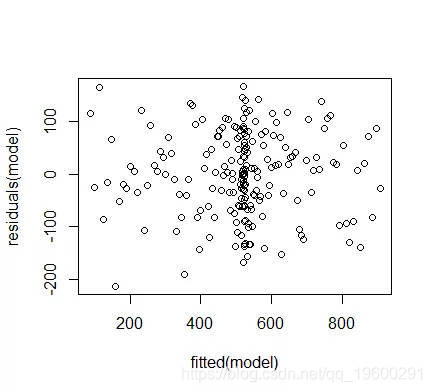
总的来说，这个模型似乎很适合，因为R的平方为0.8。正如我们所预期的那样，一阶和三阶项的系数在统计上显着。
预测值和置信区间
将线添加到现有图中：
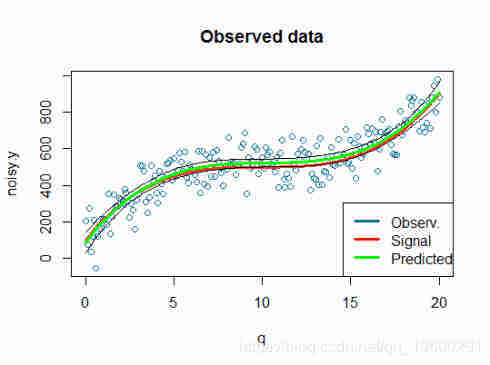
我们可以看到，我们的模型在拟合数据方面做得不错。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
R语言混合模型回归GBTM群组轨迹模型绘图可视化研究
R语言非参数回归预测摩托车事故、收入数据：局部回归、核回归、LOESS可视化
【视频讲解】非参数重采样bootstrap的逻辑回归Logistic应用及模型差异Python实现
Python个人收入影响因素模型构建：回归、决策树、梯度提升、岭回归
