逻辑回归是拟合回归曲线的方法，当y是分类变量时，y = f（x）。
典型的使用这种模型被预测Ÿ给定一组预测的X。预测因子可以是连续的，分类的或两者的混合。
可下载资源
R中的逻辑回归实现
R可以很容易地拟合逻辑回归模型。要调用的函数是glm()，拟合过程与线性回归中使用的过程没有太大差别。在这篇文章中，我将拟合一个二元逻辑回归模型并解释每一步。
数据集
我们将研究泰坦尼克号数据集。这个数据集有不同版本可以在线免费获得，但我建议使用Kaggle提供的数据集。
logistic回归的因变量可以是二分类的，也可以是多分类的，但是二分类的更为常用，也更加容易解释，多类可以使用softmax方法进行处理。实际中最为常用的就是二分类的logistic回归。
数据集（训练）是关于一些乘客的数据集合，并且竞赛的目标是预测生存（如果乘客幸存，则为1，否则为0）基于某些诸如服务等级，性别，年龄等特征。正如您所看到的，我们将使用分类变量和连续变量。
数据清理过程
在处理真实数据集时，我们需要考虑到一些数据可能丢失的事实，因此我们需要为我们的分析准备数据集。作为第一步，我们使用该函数加载csv数据read.csv()。
确保参数na.strings等于c(“”)使每个缺失值编码为a NA。这将帮助我们接下来的步骤。
training.data.raw < - read.csv（'train.csv'，header = T，na.strings = c（“”））现在我们需要检查缺失的值，并查看每个变量的唯一值，使用sapply()函数将函数作为参数传递给数据框的每一列。
sapply（training.data.raw，function（x）sum（is.na（x）））对缺失值进行可视化处理可能会有所帮助 ，可以绘制数据集并突出显示缺失值：
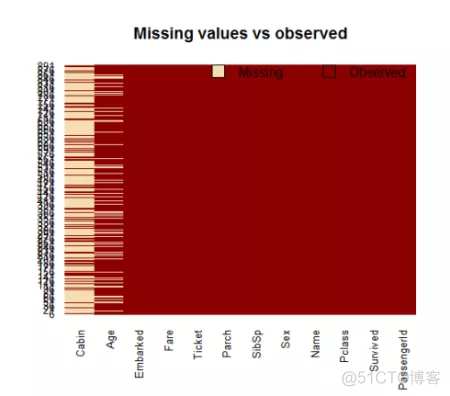
可变机舱有太多的缺失值，我们不会使用它。
使用subset()函数我们对原始数据集进行子集化，只选择相关列。
data < - subset（training.data.raw，select = c（2,3,5,6,7,8,10,12））现在我们需要解释其他缺失的值。通过在拟合函数内设置参数来拟合广义线性模型时，R可以很容易地处理它们。但是，我个人更倾向于在可能的情况下更换NAs“手动”。有不同的方法可以做到这一点，一种典型的方法是用现有的平均值，中位数或模式代替缺失值。我将使用平均值。
data$ Age [is.na（data $ Age）] < - mean（data$ Age，na.rm = T）
就分类变量而言，使用read.table()或read.csv()默认会将分类变量编码为因子。一个因素是R如何处理分类变量。
为了更好地理解R如何处理分类变量，我们可以使用该contrasts()函数。这个函数将告诉我们变量如何被R虚拟化，以及如何在模型中解释它们。
在进行拟合过程之前，让我提醒您清洁和格式化数据的重要性。这个预处理步骤对于获得模型的良好拟合和更好的预测能力通常是至关重要的。
模型拟合
我们将数据分成两部分：训练和测试集。训练集将用于适合我们将在测试集上进行测试的模型。
model <- glm(Survived ~.,family=binomial(link='logit'),data=train)
通过使用函数，summary()我们获得了我们模型的结果：
Deviance Residuals:
Min 1Q Median 3Q Max
-2.6064 -0.5954 -0.4254 0.6220 2.4165
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 5.137627 0.594998 8.635 < 2e-16 ***
Pclass -1.087156 0.151168 -7.192 6.40e-13 ***
Sexmale -2.756819 0.212026 -13.002 < 2e-16 ***
Age -0.037267 0.008195 -4.547 5.43e-06 ***
SibSp -0.292920 0.114642 -2.555 0.0106 *
Parch -0.116576 0.128127 -0.910 0.3629
Fare 0.001528 0.002353 0.649 0.5160
EmbarkedQ -0.002656 0.400882 -0.007 0.9947
EmbarkedS -0.318786 0.252960 -1.260 0.2076
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1065.39 on 799 degrees of freedom
Residual deviance: 709.39 on 791 degrees of freedom
AIC: 727.39
Number of Fisher Scoring iterations: 5解释我们的逻辑回归模型的结果
现在我们可以分析拟合并解释模型告诉我们什么。
首先，我们可以看到SibSp，Fare和Embarked没有统计意义。至于统计上显着的变量，性别具有最低的p值，这表明乘客的性别与存活的可能性有很强的关联。该预测因子的负系数表明所有其他变量相同，男性乘客不太可能存活下来。请记住，在Logit模型中，响应变量是对数可能性：ln（odds）= ln（p /（1-p））= a * x1 + b * x2 + … + z * xn。由于男性是虚拟变量，因此男性将对数赔率降低2.75，而单位年龄增加则将对数赔率降低0.037。
现在我们可以运行anova()模型上的函数来分析偏差表
现在我们可以运行anova()模型上的函数来分析偏差表
Analysis of Deviance Table
Model: binomial, link: logit
Response: Survived
Terms added sequentially (first to last)
Df Deviance Resid. Df Resid. Dev Pr(>Chi)
NULL 799 1065.39
Pclass 1 83.607 798 981.79 < 2.2e-16 ***
Sex 1 240.014 797 741.77 < 2.2e-16 ***
Age 1 17.495 796 724.28 2.881e-05 ***
SibSp 1 10.842 795 713.43 0.000992 ***
Parch 1 0.863 794 712.57 0.352873
Fare 1 0.994 793 711.58 0.318717
Embarked 2 2.187 791 709.39 0.334990
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1零偏差和剩余偏差之间的差异显示了我们的模型如何对付零模型（仅包含截距的模型）。这个差距越大越好。通过分析表格，我们可以看到每次添加一个变量时出现偏差的情况。同样，增加Pclass，Sex and Age可以显着减少残余偏差。尽管SibSp具有较低的p值，但其他变量似乎可以减少模型。这里的大p值表示没有变量的模型或多或少地解释了相同的变化量。最终你想看到的是一个显着的下降和偏差AIC。
尽管不存在与线性回归的R 2确切等价，但McFadden R 2指数可用于评估模型拟合。
评估模型的预测能力
在上面的步骤，我们简要评价模型的拟合，现在我们希望看到，当预测模型是如何做Ÿ在新的一组数据。通过设置参数type=’response’，R将以P（y = 1 | X）的形式输出概率。我们的决策边界将是0.5。如果P（y = 1 | X）> 0.5，则y = 1，否则y = 0。请注意，对于某些应用程序，不同的阈值可能是更好的选择。
misClasificError <- mean(fitted.results != test$Survived)
print(paste('Accuracy',1-misClasificError))
"Accuracy 0.842696629213483"测试集上的0.84精度是相当不错的结果。但是，请记住，这个结果有点依赖于我之前做的数据的手动分割，因此如果您希望得到更精确的分数，最好运行某种交叉验证，如k折叠交叉验证验证。
作为最后一步，我们将绘制ROC曲线并计算二元分类器典型性能测量的AUC（曲线下面积）。
ROC是通过在各种阈值设置下将真阳性率（TPR）与假阳性率（FPR）作图而产生的曲线，而AUC是ROC曲线下的面积。作为一个经验法则，具有良好预测能力的模型应该具有接近于1（1是理想的）的AUC比0.5。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
【视频讲解】非参数重采样bootstrap的逻辑回归Logistic应用及模型差异Python实现
过采样SMOTE逻辑回归、SVM、随机森林、AdaBoost和XGBoost对不平衡数据分析预测
【视频讲解】逻辑回归原理及R语言预测心脏病、用户流失数据挖掘2实例
SPSS用CHAID决策树、逻辑回归预测电信用户产品使用流失数据
