
在普遍的理解中,最大似然估计是使用已知的样本结果信息来反向推断最有可能导致这些样本结果的模型参数值!
换句话说,最大似然估计提供了一种在给定观测数据的情况下评估模型参数的方法,即“模型已确定且参数未知”。
在所有双射函数的意义上,极大似然估计是不变的 ,如果
是
的极大似然估计
。
让 ,
等于
中的似然函数。由于
是的最大似然估计
,
因此, 是
的最大似然估计 。
×
最大似然估计:现在已经拿到了很多个样本(你的数据集中所有因变量),这些样本值已经实现,最大似然估计就是去找到那个(组)参数估计值,使得前面已经实现的样本值发生概率最大。因为你手头上的样本已经实现了,其发生概率最大才符合逻辑。这时是求样本所有观测的联合概率最大化,是个连乘积,只要取对数,就变成了线性加总。此时通过对参数求导数,并令一阶导数为零,就可以通过解方程(组),得到最大似然估计值。
最小二乘:找到一个(组)估计值,使得实际值与估计值的距离最小。本来用两者差的绝对值汇总并使之最小是最理想的,但绝对值在数学上求最小值比较麻烦,因而替代做法是,找一个(组)估计值,使得实际值与估计值之差的平方加总之后的值最小,称为最小二乘。“二乘”的英文为least square,其实英文的字面意思是“平方最小”。这时,将这个差的平方的和式对参数求导数,并取一阶导数为零,就是OLSE。
最小二乘:找到一个(组)估计值,使得实际值与估计值的距离最小。本来用两者差的绝对值汇总并使之最小是最理想的,但绝对值在数学上求最小值比较麻烦,因而替代做法是,找一个(组)估计值,使得实际值与估计值之差的平方加总之后的值最小,称为最小二乘。“二乘”的英文为least square,其实英文的字面意思是“平方最小”。这时,将这个差的平方的和式对参数求导数,并取一阶导数为零,就是OLSE。
例如,伯努利分布为 ,
给定样本 ,概率是
则对数似然
与ICI
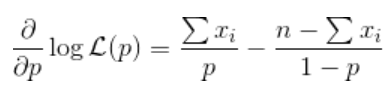
因此,一阶条件
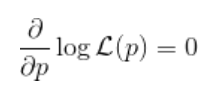
何时满足 。为了说明,考虑以下数据
> X
[1] 0 0 1 1 0 1 1 1 1 0 0 0 1 0 1(负)对数似然
> loglik=function(p){
+ -sum(log(dbinom(X,size=1,prob=p)))
+ }我们可以在下面看到
> plot(u,v,type="l",xlab="",ylab="")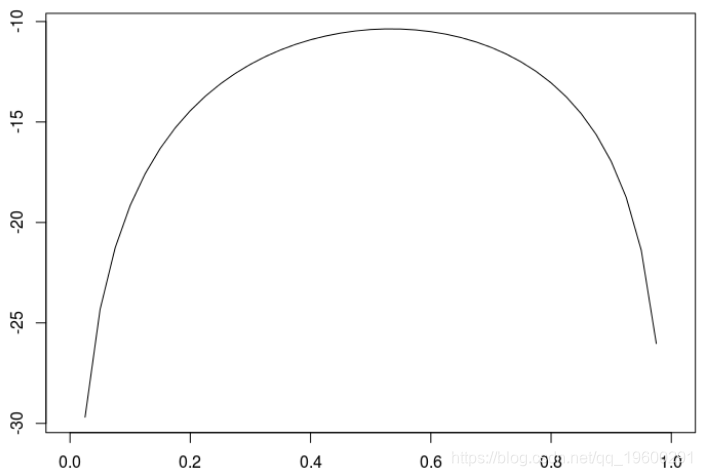
根据以上计算,我们知道的极大似然估计 是
> mean(X)
[1] 0.53数值为
$par
[1] 0.53
$value
[1] 10.36
$counts
function gradient
20 NA
$convergence
[1] 0
$message
NULL我们没有说优化是在区间内 。但是,我们的概率估计值属于
。为了确保最优值在
,我们可以考虑一些约束优化程序
ui=matrix(c(1,-1),2,1), ci=c(0,-1)
$par
[1] 0.53
$value
[1] 10.36
$counts
function gradient
20 NA
$convergence
[1] 0
$message
NULL
$outer.iterations
[1] 2
$barrier.value
[1] 6.91e-05在上一张图中,我们达到了对数似然的最大值
> abline(v=opt$par,col="red")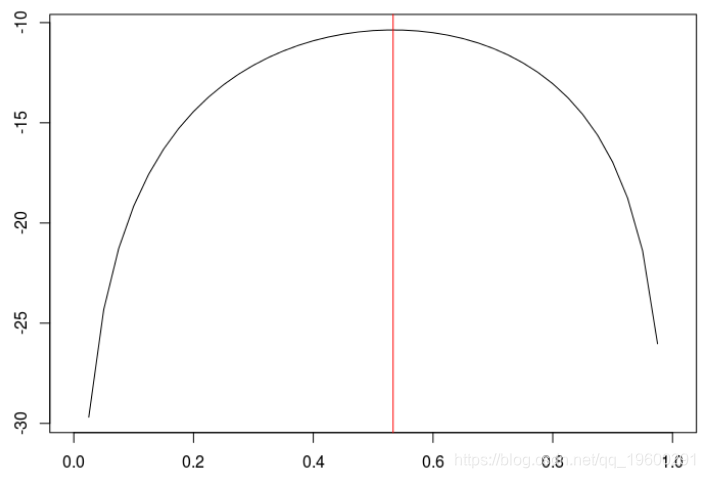
另一种方法是考虑 (如指数分布)。则对数似然
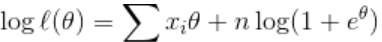
这里
因此,一阶条件
满足
从数值角度来看,我们有相同的最优值
(opt=optim(0,loglik))
$par
[1] 0.13
$value
[1] 10.36
$counts
function gradient
20 NA
$convergence
[1] 0
$message
NULL
> exp(opt$par)/(1+exp(opt$par))
[1] 0.53


 R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据
R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据 R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据
R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据 视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析
视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析 高维变量选择专题|R、Python用HOLP、Lasso、SCAD、PCR、ElasticNet实例合集分析企业财务、糖尿病、基因数据
高维变量选择专题|R、Python用HOLP、Lasso、SCAD、PCR、ElasticNet实例合集分析企业财务、糖尿病、基因数据



