在统计学习和机器学习的领域中,逻辑回归模型是一种广泛应用于分类问题的预测模型。
特别是在预测二分类事件或情况时,如选举中某党派是否获得投票、用户是否购买某产品、个体是否感染某种疾病等,逻辑回归模型展现出了其独特的优势。
本文将通过视频讲解,展示逻辑回归模型原理,并结合一个PYTHON用户流失数据挖掘:建立逻辑回归、XGBOOST、随机森林、决策树、支持向量机、朴素贝叶斯模型和KMEANS聚类用户画像和R语言逻辑回归、Naive Bayes贝叶斯、决策树、随机森林算法预测心脏病的代码数据,为读者提供一套完整的实践数据分析流程。
什么是逻辑回归模型?
逻辑回归模型本质上是一种概率模型,用于预测某一事件或情况发生的概率。其因变量为二分变量,通常用0和1表示,其中0代表事件不发生,1代表事件发生。
可下载资源
作者
视频
【视频讲解】逻辑回归原理及R语言预测心脏病、用户流失数据挖掘2实例
与线性回归不同,逻辑回归的输出被限制在0和1之间,通过逻辑函数(如Sigmoid函数)将线性回归的预测值转换为概率值。当预测的概率低于设定的阈值(通常为0.5)时,模型将事件归类为0;反之,则归类为1。
模型原理
逻辑回归模型通过训练数据学习自变量与因变量之间的关系,并构建出能够预测新数据点因变量取值的模型。该模型的核心是逻辑函数,它将线性回归的预测值转换为概率值,从而使得模型的输出符合二分变量的特性。
Metrics(衡量)
在评估逻辑回归模型的性能时,我们通常使用准确率、召回率、F1分数等指标。这些指标能够全面反映模型在分类任务中的表现,帮助我们更好地理解和优化模型。
重要变量
在逻辑回归模型中,自变量(或称为特征)的选择对于模型的性能至关重要。
重要变量通常与因变量具有较强的相关性,能够显著提高模型的预测能力。通过特征选择和特征工程等技术,我们可以从原始数据中提取出对模型有用的信息,进一步提高模型的性能。
Linear Regression的区别
逻辑回归与线性回归在多个方面存在显著差异。首先,逻辑回归的因变量是分类变量,而线性回归的因变量是连续变量。其次,逻辑回归的输出被限制在0和1之间,而线性回归的输出则没有这样的限制。此外,逻辑回归的模型参数具有直观的解释性,可以表示自变量对因变量影响的程度和方向。
优缺点分析
逻辑回归模型具有以下优点:
处理分类变量:逻辑回归能够处理因变量为分类变量的问题,这是线性回归无法做到的。直观解释:逻辑回归的模型参数具有直观的解释性,可以帮助我们理解自变量对因变量的影响。低方差:当特征较少而数据量较大时,逻辑回归往往具有较低的方差,不易过拟合。训练速度快:逻辑回归模型的训练过程相对简单,计算效率较高。
随时关注您喜欢的主题
然而,逻辑回归也存在一些缺点:
- 不能处理不平衡数据:当正负样本数量差异较大时,逻辑回归的性能可能会受到影响。
- 分类仅限于二分:逻辑回归只能处理二分类问题,对于多分类问题需要进行额外的处理。
- 假设自变量间相互独立:逻辑回归假设自变量间相互独立,难以处理多重共线性问题。在实际应用中,这可能需要通过特征选择或降维等技术来避免。
PYTHON用户流失数据挖掘:建立逻辑回归、XGBOOST、随机森林、决策树、支持向量机、朴素贝叶斯和KMEANS聚类用户画像
在今天产品高度同质化的品牌营销阶段,企业与企业之间的竞争集中地体现在对客户的争夺上。“用户就是上帝”促使众多的企业不惜代价去争夺尽可能多的客户。但是企业在不惜代价发展新用户的过程中,往往会忽视或无暇顾及已有客户的流失情况,结果就导致出现这样一种窘况:一边是新客户在源源不断地增加,而另一方面是辛辛苦苦找来的客户却在悄然无声地流失。
可下载资源
1 概述
1.1 项目背景:
因此对老用户的流失进行数据分析从而挖掘出重要信息帮助企业决策者采取措施来减少用户流失的事情至关重要,迫在眉睫。

1.2 目的:
一是寻找关键因子,比如探索用户离网的影响因素,根据影响因素判断用户离网发生的概率。通过研究现有套餐产品客户在呼叫通话、业务使用等各方面的行为特征,找到关键影响因子;
二是构建预测模型:采用数据挖掘监督类模型技术,训练得到潜在客户预测模型,用于预测将会选择该类套餐产品的潜在流失用户群,并以概率形式量化之。如果已经建立了Logistic回归模型,则可以根据模型,预测在不同的自变量情况下,客户流失的概率有多大;
三是判别:实际上跟预测有些类似,根据Logistic模型,判断客户有多大的可能性将会流失。这种技术与线性回归类似,只是用分类目标字段代替了数值字段,而在目标含有两个截然不同的类别时可以使用二项模型;
四是推送营业前台:通过营销管理平台,直接将高概率产品目标流失客户群推送到营业厅、短信及网站、社区经理等营销渠道,将挽留策略和产品在合适的时间、以合适的语言推荐给合适的客户,从而赢得营销。
客户流失模型需要完成两个方面的任务,即分析流失客户的特征,导致客户流失的因素及客户流失在这些因素上的分布情况,还有就是得出潜在的流失客户群。
深入了解用户画像及行为偏好,挖掘出影响用户流失的关键因素,并通过算法预测客户访问的转化结果,从而更好地完善产品设计、提升用户体验。
1.3 数据说明:
此次数据是携程用户一周的访问数据,为保护客户隐私,已经将数据经过了脱敏,和实际商品的订单量、浏览量、转化率等有一些差距,不影响问题的可解性。
2 读取数据
==========
# 显示全部特征 df.head()
视频
Boosting集成学习原理与R语言提升回归树BRT预测短鳍鳗分布生态学实例
视频
逻辑回归Logistic模型原理和R语言分类预测冠心病风险实例

3 切分数据
# 划分训练集,测试集 X\_train, X\_test, y\_train, y\_test = train\_test\_split(X, y, test\_size=0.2, random\_state=666)
3.1 理解数据
可以看到变量比较的多,先进行分类,除去目标变量label,此数据集的字段可以分成三个类别:订单相关指标、客户行为相关指标、酒店相关指标。

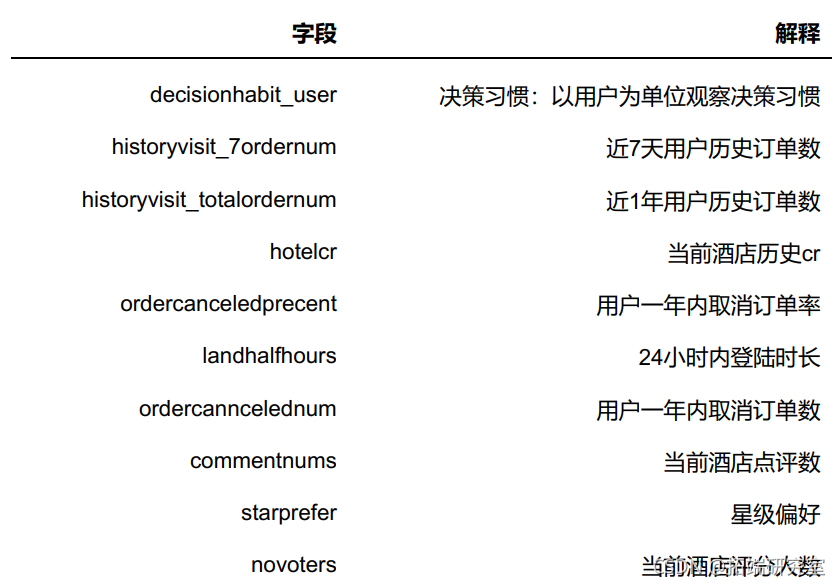
4 特征工程
# 用训练集进行数据探索 train = pd.concat(\[X\_train,y\_train\],axis=1)
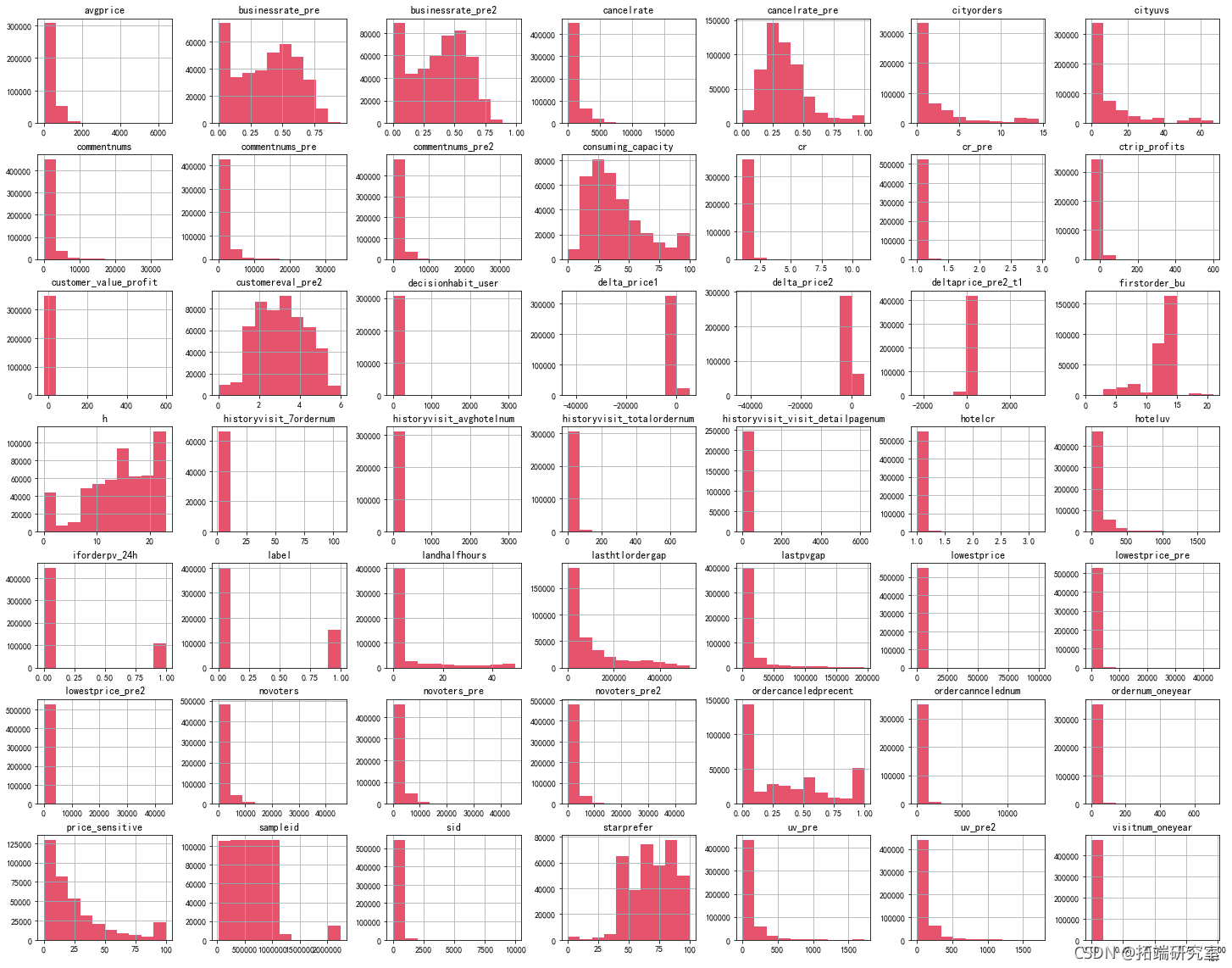
4.1 数据预处理

4.1.1 删除不必要的列
X_train.pop("sampleid")
X_test.pop("sampleid")
train.pop("sampleid")

4.1.2 数据类型转换
字符串类型的特征需要处理成数值型才能建模,将arrival和d相减得到”提前预定的天数”,作为新的特征
# 增加列 # 将两个日期变量由字符串转换为日期格式类型 train\["arrial"\] = pd.to_datimetain\["arrval"\]) X\_tst\["arival"\] = d.to\_daetime(X_est\["arival"\]) # 生成提前预定时间列(衍生变量) X\_trin\["day\_adanced"\] = (X_rain\["arival"\]-Xtrain\["d"\]).dt.days ## 删除列 X_tran.dro(columns="d","arrivl"\],inpace=True)
4.1.3 缺失值的变量生成一个指示哑变量
============================
zsl = tain.isnll().sum()\[tain.isnll(.sum()!=0\].inex
4.1.4 根据业务经验填补空缺值
ordernum_oneyear 用户年订单数为0 ,lasthtlordergap 11%用600000填充 88%用600000填充 一年内距离上次下单时长,ordercanncelednum 用0填充 用户一年内取消订单数,ordercanceledprecent 用0t填充 用户一年内取消订单率 242114 242114 -为空 有2种情况 1:新用户未下订单的空-88.42% 214097 2.老用户1年以上未消费的空 增加编码列未下订单新用户和 1年未下订单的老用户
tkq = \["hstoryvsit\_7ordernm","historyviit\_visit\_detaipagenum","frstorder\_b","historyvi # tbkq = \["hitoryvsit\_7dernum","hisryvisit\_isit_detailagenum"\] X_train\[i\].fillna(0,inplace=True)
## 一部分用0填充,一部分用中位數填充 # 新用戶影響的相關屬性:ic\_sniti,cosuing\_cacity n\_l = picesensitive","onsmng\_cpacty"\] fori in n_l X\_trini\]\[Xra\[X\_trinnew_ser==1\].idex\]=0 X\_est\[i\]\[X\_test\[X\_test.nw\_user==1\].inex\]=0
4.1.5 异常值处理
将customer\_value\_profit、ctrip_profits中的负值按0处理
将delta\_price1、delta\_price2、lowestprice中的负值按中位数处理
uv\_pre -24小时历史浏览次数最多酒店历史uv. cr\_pre -0,中位数填充 -24小时历史浏览次数最多酒店历史cr -0,中位数填充 29397 -为空 1.用户当天未登录APP 28633 2.刚上线的新酒店178 586 无uv,cr记录 编码添加 该APP刚上线的新酒店 764 29397
customereval_pre2 用0填充-24小时历史浏览酒店客户评分均值, landhalfhours -24小时内登陆时长 -用0填充28633 -为空:用户当天未登录APP 28633
hotelcr ,hoteluv -中位数填充 797
刚上新酒店 60 #未登录APP 118
avgprice 0 填充一部分价格填充为0 近一年未下过订单的人数,cr 用0填充,
price\_sensitive -0 ,中位数填充 价格敏感指数,consuming\_capacity -0 中位数填充 消费能力指数 226108 -为空情况 1.从未下过单的新用户214097 2.12011个人为空原因暂不明确
for f in flter_two: a = X_trin\[\].median() X\_tran\[f\]\[X\_train\[f\]<0\]=a X\_test\[f\]\[X\_est\[\]<0\]=a tran\[f\]\[train\[f\]<0\]=a
4.1.6 缺失值填充
趋于正态分布的字段,使用均值填充:businessrate\_pre2、cancelrate\_pre、businessrate_pre;偏态分布的字段,使用中位数填充.
def na_ill(df): for col in df.clumns: mean = X_trai\[col\].mean() dfcol\]=df\[col\].fillna(median) return
## 衍生变量年成交率 X\_train\["onear\_dalate"\]=\_tain\["odernum\_onyear"\]/X\_tran"visinum\_onyar"\] X\_st\["onyardealae"\]=X\_st\["orernum_neyear"\]/Xtest\[visitumonyear"\] X_al =pd.nca(\[Xtin,Xtes)
#决策树检验 dt = Decsionr(random_state=666) pre= dt.prdict(X_test) pre\_rob = dt.preicproa(X\_test)\[:,1\] pre_ob

4.2 数据标准化
================
scaler = MinMacaer() #决策树检验 dt = DeonTreasifi(random_state=666)
5 特征筛选
5.1 特征选择-删除30%列
X\_test = X\_test.iloc\[:,sp.get_spport()\] #决策树检验 dt = DecisonreeClssifie(random_state=666) dt.fit(X\_trin,y\_tain) dt.score(X\_tst,y\_est) pre = dt.pdict(X_test) pe\_rob = dt.redicproba(X\_test)\[:,1\] pr_rob uc(pr,tpr)

5.2 共线性/数据相关性
#共线性--严重共线性0.9以上,合并或删除 d = Xtrai.crr() d\[d<0.9\]=0 #赋值显示高相关的变量 pl.fufsiz=15,15,dpi200) ssheatp(d)
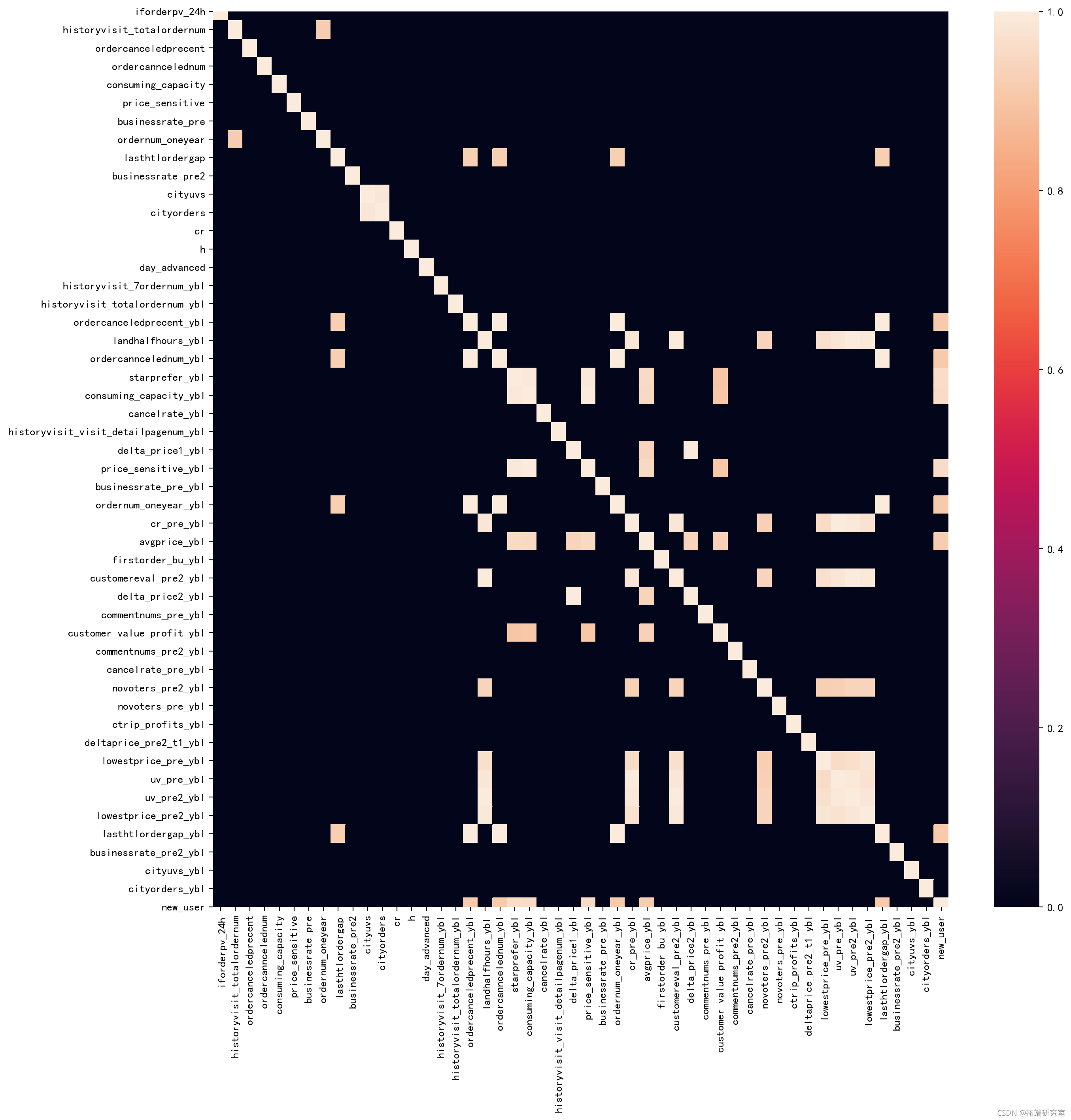
6 建模与模型评估
6.1 逻辑回归
随时关注您喜欢的主题
y\_prob = lr.preictproba(X\_test)\[:,1\]
y\_pred = lr.predict(X\_test
fpr\_lr,pr\_lr,teshold\_lr = metris.roc\_curve(y\_test,y\_prob)
ac\_lr = metrcs.aucfpr\_lr,tpr_lr)
score\_lr = metrics.accuracy\_score(y\_est,y\_pred)
prnt("模准确率为:{0},AUC得分为{1}".fomat(score\_lr,auc\_lr))
prit("="*30
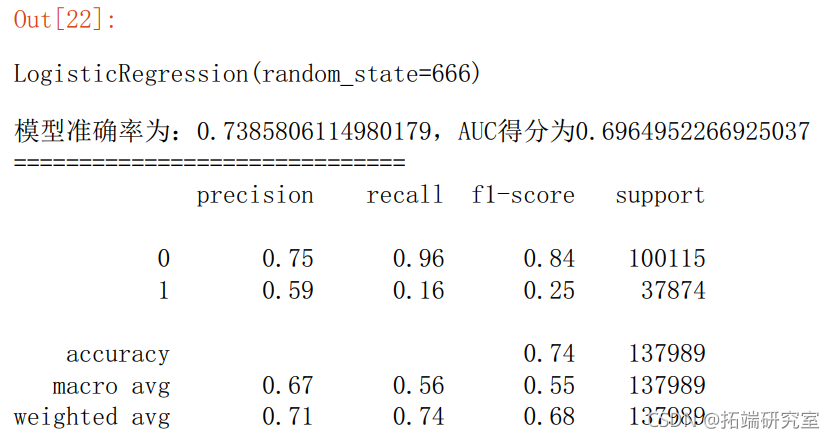
6.2 朴素贝叶斯
gnb = GasinNB() # 实例化一个LR模型 gnb.fi(trai,ytran) # 训练模型 y\_prob = gn.pic\_proba(X_test)\[:,1\] # 预测1类的概率 y\_pred = gnb.preict(X\_est) # 模型对测试集的预测结果 fpr\_gnb,tprgnbtreshold\_gb = metrics.roc\_crve(ytesty\_pob) # 获取真阳率、伪阳率、阈值 aucgnb = meic.aucf\_gnb,tr\_gnb) # AUC得分 scoe\_gnb = merics.acuray\_score(y\_tes,y\_pred) # 模型准确率
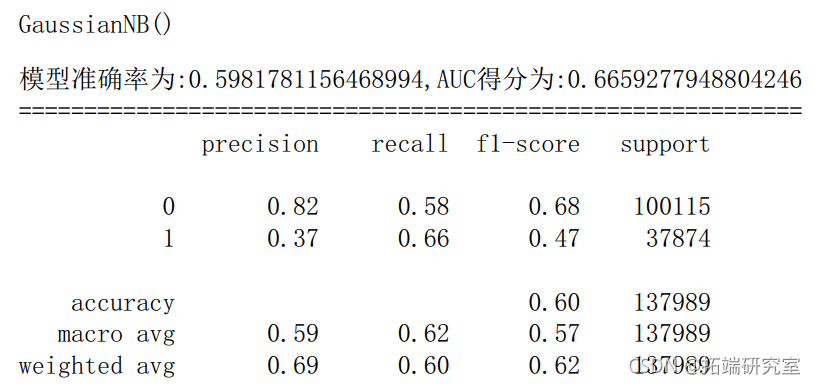
6.3 支持向量机
s =SVkernel='f',C=,max_ter=10,randomstate=66).fit(Xtrain,ytrain) y\_rob = sc.decsion\_untio(X_st) # 决策边界距离 y\_ed =vc.redit(X\_test) # 模型对测试集的预测结果 fpr\_sv,tpr\_vc,theshld\_sv = mtris.rc\_urv(y\_esty\_pob) # 获取真阳率、伪阳率、阈值 au\_vc = etics.ac(fpr\_sc,tpr_sv) # 模型准确率 scre\_sv = metrics.ccuracy\_sore(_tst,ypre)
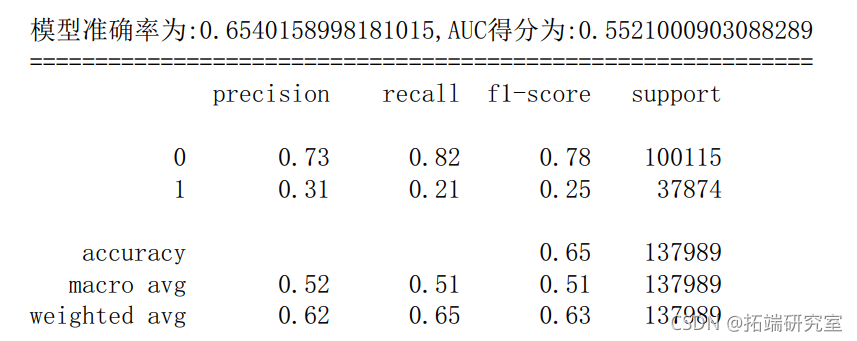
6.4 决策树
dtc.fit(X\_tran,\_raiproba(X_test)\[:,1\] # 预测1类的概率 y\_pred = dtc.predct(X\_test # 模型对测试集的预测结果 fpr\_dtc,pr\_dtc,thresod\_dtc= metrcs.roc\_curvey_test,yprob) # 获取真阳率、伪阳率、阈值
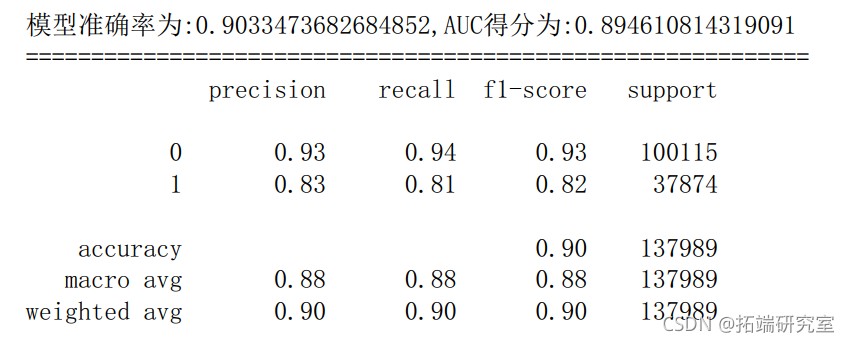
6.5 随机森林
c = RndoForetlassiir(rand_stat=666) # 建立随机森 rfc.it(X_tain,ytrain) # 训练随机森林模型 y\_rob = rfc.redict\_poa(X_test)\[:,1\] # 预测1类的概率 y\_pedf.pedic(\_test) # 模型对测试集的预测结果 fpr\_rfc,tp\_rfc,hreshol\_rfc = metrcs.roc\_curve(y\_test,\_prob) # 获取真阳率、伪阳率、阈值 au\_fc = meris.auc(pr\_rfctpr_fc) # AUC得分 scre\_rf = metrcs.accurac\_scor(y\_tes,y\_ped) # 模型准确率
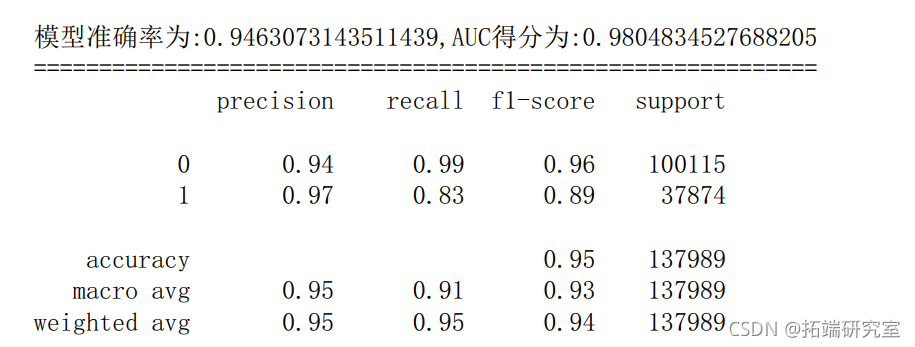
6.6 XGboost
# 读训练数据集和测试集
dtainxgbatrx(X_rai,yrain)
dtest=g.DMrx(Xtest
# 设置xgboost建模参数
paras{'booser':'gbtee','objective': 'binay:ogistic','evlmetric': 'auc'
# 训练模型
watchlst = (dtain,'trai)
bs=xgb.ran(arams,dtain,n\_boost\_round=500eva=watchlst)
# 输入预测为正类的概率值
y_prob=bst.redict(dtet)
# 设置阈值为0.5,得到测试集的预测结果
y\_pred = (y\_prob >= 0.5)*1
# 获取真阳率、伪阳率、阈值
fpr\_xg,tpr\_xgb,heshold\_xgb = metricsroc\_curv(test,y_prob)
aucxgb= metics.uc(fpr\_gb,tpr\_xgb # AUC得分
score\_gb = metricsaccurac\_sore(y\_test,y\_pred) # 模型准确率
print('模型准确率为:{0},AUC得分为:{1}'.format(score\_xgb,auc\_xgb))

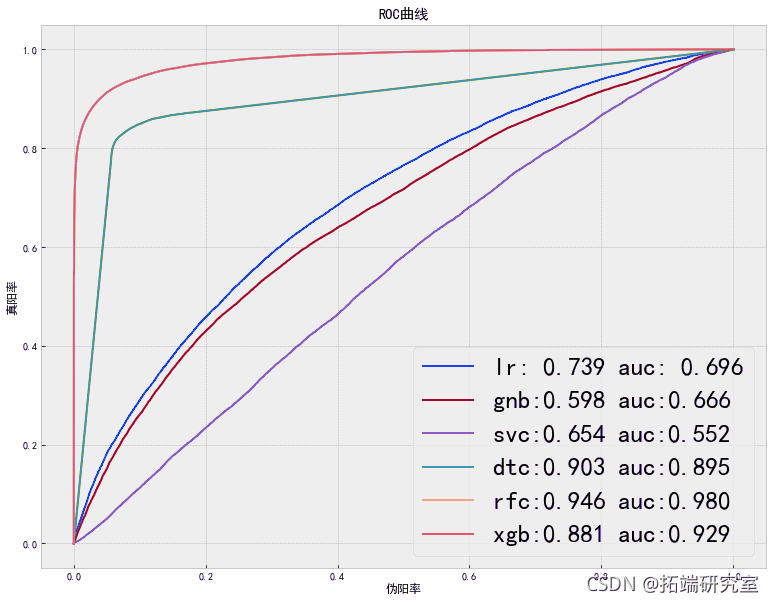
6.7 模型比较
plt.xlabel('伪阳率')
plt.ylabel('真阳率')
plt.title('ROC曲线')
plt.savefig('模型比较图.jpg',dpi=400, bbox_inches='tight')
plt.show()
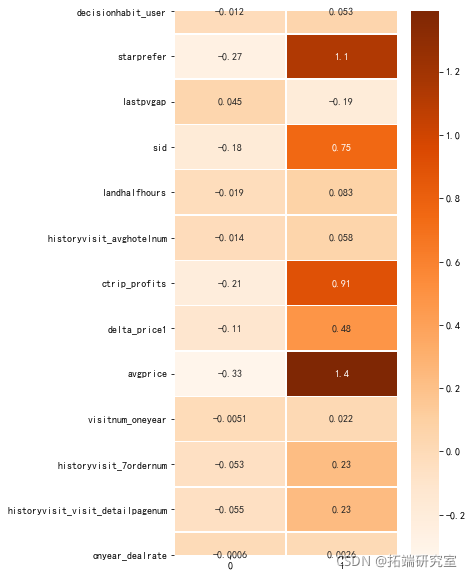
6.8 重要特征
ea = pd.Sries(dct(list((X\_trclumsfc.eatre\_imortancs_)))) ea.srt_vlues(acedig=False fea\_s = (fa.srt\_vauesacnding=alse)).idex

====================================================================================================================================================================================================================

6.9 流失原因分析
- cityuvs和cityorders值较小时用户流失显著高于平均水平,说明携程平台小城市的酒店信息缺乏,用户转向使用小城市酒店信息较全的竞品导致用户流失
- 访问时间点在7点-19点用户流失比例高与平均水平:工作日推送应该避开这些时间点
- 酒店商务属性指数在0.3-0.9区间内用户流失大于平均水平,且呈现递增趋势,说明平台商务指数高的酒店和用户期望有差距(价格太高或其他原因?), 商务属性低的用户流失较少
- 一年内距离上次下单时长越短流失越严重,受携程2015年5月-2016年1月爆出的负面新闻影响较大,企业应该更加加强自身管理,树立良好社会形象
- 消费能力指数偏低(10-40)的用户流失较严重,这部分用户占比50%应该引起重视
- 价格敏感指数(5-25)的人群流失高于平均水平,注重酒店品质
- 用户转化率,用户年订单数,近1年用户历史订单数越高,24小时内否访问订单填写页的人群比例越大流失越严重,需要做好用户下单后的追踪体验, 邀请填写入住体验,整理意见作出改进
提前预定天数越短流失越严重用户一年内取消订单数越高流失越严重
6.10 建议:
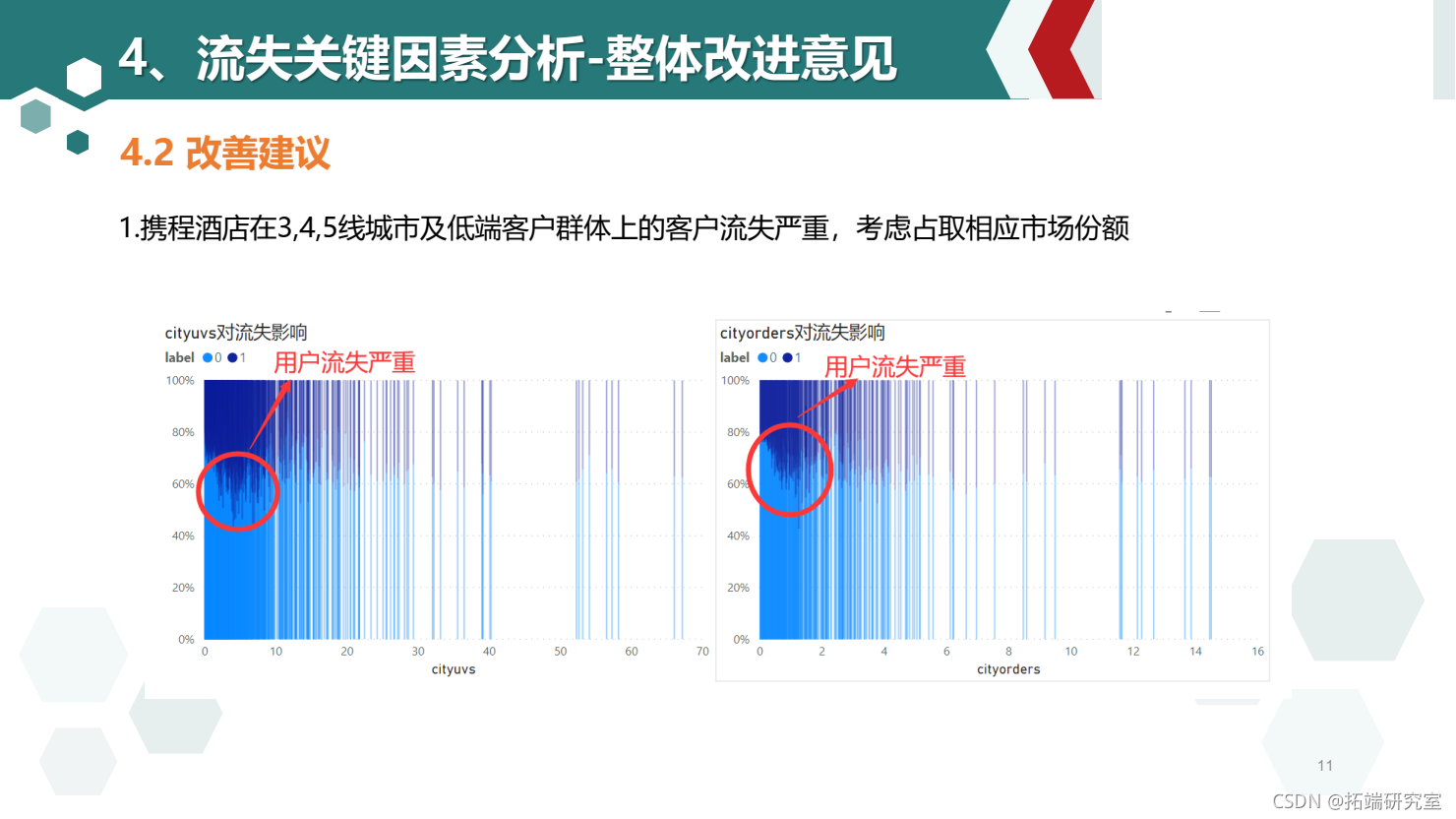
- 考虑占取三四线城市和低端酒店范围的市场份额
- 用户易受企业负面新闻影响,建议企业勇于承担社会责任,加强自身管理,提高公关新闻处理时效性,树立品牌良好形像
- 在节假日前2-3周开始热门景点酒店推送
- 做好酒店下单后的追踪体验,邀请填写入住体验,并整理用户意见作出改进
客户画像
7.1 建模用户分类
# 用户画像特征 user\_feature = \["decisiohabit\_user,'starprefer','lastpvgap','sid', 'lernum",'historyvisit\_visit\_detaipagenum', "onyear_dealrat \] # 流失影响特征 fea_lis = \["cityuvs", "cityorders", "h", "businessrate_pre2" # 数据标准化 Kmeans方法对正态分布数据处理效果更好 scaler = StanardScalr() lo\_atribues = pdDatarame(scr.fittransfrm(all\_cte),columns=all_ce.coluns) # 建模分类 Kmens=Means(n\_cluste=2,rndom\_state=0) #333 Keans.fi(lot_attributes # 训练模型 k\_char=Kmenscluster\_centers_ # 得到每个分类 plt.figure(figsize=(5,10))

7.2 用户类型占比
==============
types=\['高价值用户','潜力用户'\] ax.pie\[1\], raius=0.,colors='w') plt.savefig(用户画像.jpg'dpi=400, box_inchs='tigh')
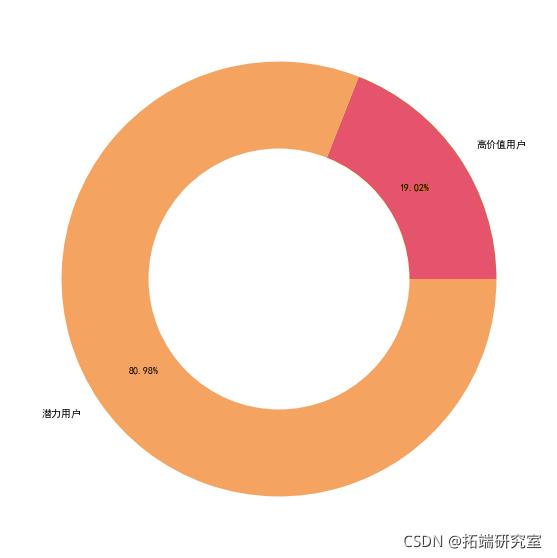
7.3 高价值用户分析 :
占比19.02,访问频率和预定频率都较高,消费水平高,客户价值大,追求高品质,对酒店星级要求高,客户群体多集中在老客户中,
建议:
多推荐口碑好、性价比高的商务酒店连锁酒店房源吸引用户;
在非工作日的11点、17点等日间流量小高峰时段进行消息推送。
为客户提供更多差旅地酒店信息;
增加客户流失成本:会员积分制,推出会员打折卡
7.4 潜力用户分析
占比:80.98% 访问频率和预定频率都较低,消费水平较低,对酒店星级要求不高,客户群体多集中在新客户中,客户价值待挖掘 建议:
因为新用户居多,属于潜在客户,建议把握用户初期体验(如初期消费有优惠、打卡活动等),还可以定期推送实惠的酒店给此类用户,以培养用户消费惯性为主;
推送的内容应多为大减价、大酬宾、跳楼价之类的;
由于这部分用户占比较多,可结合该群体流失情况分析流失客户因素,进行该群体市场的开拓,进一步进行下沉分析,开拓新的时长。
R语言逻辑回归、Naive Bayes贝叶斯、决策树、随机森林算法预测心脏病
最近我们被客户要求撰写关于预测心脏病的研究报告。这个数据集可以追溯到1988年,由四个数据库组成。克利夫兰、匈牙利、瑞士和长滩。”目标 “字段是指病人是否有心脏病。它的数值为整数,0=无病,1=有病。
目标:
主要目的是预测给定的人是否有心脏病,借助于几个因素,如年龄、胆固醇水平、胸痛类型等。
我们在这个问题上使用的算法是:
- 二元逻辑回归
- Naive Bayes算法
- 决策树
- 随机森林
CUT OFF值的设定有多种不同方法。常见的方法包括:
一、使用阴性血清测定结果均值的2或3倍作为CUT OFF值
该方法是取一定数量(通常不多)的阴性血清样本,使用免疫检测试剂盒进行测定,取阴性样本的测值的平均值。若上述阴性样本的平均值为X,则该次测定的CUT OFF值为2X或3X。例如,试剂盒结果判定以S(样本测值)/N(阴性对平均测值)≥2.1为阳性,其依据即是以阴性参考血清的2.1倍作为CUT OFF值。通常为了避免阴性样本测值过低导致的CUT OFF值过低,还会规定阴性样本平均测值不到某一特定值,如0.05时,以0.05计算,即CUT OFF值不低于0.10。采用这种方法设定CUTOFF值,可以有效避免假阳性结果的出现,但易导致假阴性结果较多,是一种非常粗糙的CUT OFF值设定方法。
二、阴性对照平均测值+2个标准差(SD)或3SD作为CUT OFF值
先取大量(数千)正常人(阴性)血清样本进行检测,当阴性样本量足够大时,使用试剂盒检测所得测值将呈正态分布,若要求95.3%(单侧)的可信度,可将阴性样本平均测值+2SD作为CUT OFF值;若要求99%(单侧)的可信度,则以阴性样本平均测值+3SD作为CUT OFF值。这种方法建立在统计学计算的基础上,相比于第一种方法,更为科学。但这种方法仅考虑正常人群(阴性样本),因此难以界定“灰区”,几乎所有灰区样本都阴性结果处理,可能会出现较多假阴性。
三、综合阴性对照均值+2或3SD及阳性对照均值-2或3SD建立CUT OFF值
先测定大量阴性血清样本,若测值为正态分布,在具有95.3%(单侧)的可信度的情况下,可以将从阴性样本中得到的测值+2SD得到一侧CUT OFF值,若要求99%(单侧)的可信度,则以测值+3SD为一侧CUT OFF值。然后检测大量阳性样本,在具有95.3%(单侧)的可信度的情况下,可以将从阳样本中得到的测值-2SD得到另一侧CUTOFF值,若要求99%(单侧)的可信度,则以测值-3SD为另一侧CUT OFF值。阴性和阳性样本的CUT OFF值确定后,根据“灰区”的大小,综合平衡考虑假阳性率和假阴性率,确定试剂盒的CUT OFF值。这种方法对比方法二,对阳性人群也有考虑,并且对“灰区”的存在有一定估计,不会出现将“灰区”全部归为阴性结果的情况。
若样本测值为非正态分布,可采用“百分位数法”,以阴阳性样本测定结果的百分位数单侧95%或99%分别来确定两侧CUT OFF值,再综合平衡考虑假阳性率和假阴性率。
四、在方法三的基础上,增加检测血清转化盘样本
在检测大量阴性及阳性样本基础上,检测转化型血清(从阴性转变为阳性过程中的系列血清)样本,取假阳性和假阴性发生率最低、且能区别抗原转化至抗体出现点的吸光度值作为CUT OFF值。由此确定的CUT OFF值能有最佳区分阴阳性样本的能力。
五、ROC曲线(受试者工作曲线)法
ROC曲线是以假阳性率(1-特异性)为横坐标,真阳性率(灵敏度)为纵坐标所绘制的一条曲线,是反映敏感度和特异度连续变量的综合指标,用作图法展示两度之间的关系。
数据集的描述:
该数据有303个观察值和14个变量。每个观察值都包含关于个人的以下信息。
- 年龄:- 个人的年龄,以年为单位
- sex:- 性别(1=男性;0=女性)
- cp – 胸痛类型(1=典型心绞痛;2=非典型心绞痛;3=非心绞痛;4=无症状)。
- trestbps–静息血压
- chol – 血清胆固醇,单位:mg/dl
- fbs – 空腹血糖水平>120 mg/dl(1=真;0=假)
- restecg – 静息心电图结果(0=正常;1=有ST-T;2=肥大)
- thalach – 达到的最大心率
- exang – 运动诱发的心绞痛(1=是;0=否)
- oldpeak – 相对于静止状态,运动诱发的ST压低
- slope – 运动时ST段峰值的斜率(1=上斜;2=平坦;3=下斜)
- ca – 主要血管的数量(0-4),由Flourosopy着色
- 地中海贫血症–地中海贫血症是一种遗传性血液疾病,会影响身体产生血红蛋白和红细胞的能力。1=正常;2=固定缺陷;3=可逆转缺陷
- 目标–预测属性–心脏疾病的诊断(血管造影疾病状态)(值0=<50%直径狭窄;值1=>50%直径狭窄)
在Rstudio中加载数据
可下载资源
视频
贝叶斯推断线性回归与R语言预测工人工资数据
视频
逻辑回归Logistic模型原理和R语言分类预测冠心病风险实例
heart<-read.csv("heart.csv",header = T)header = T意味着给定的数据有自己的标题,或者换句话说,第一个观测值也被考虑用于预测。
head(heart)
当我们想查看和检查数据的前六个观察点时,我们使用head函数。
tail(heart)
显示的是我们数据中最后面的六个观察点
colSums(is.na(heart))
这个函数是用来检查我们的数据是否包含任何NA值。
如果没有发现NA,我们就可以继续前进,否则我们就必须在之前删除NA。
检查我们的数据结构
str(heart)
查看我们的数据摘要
summary(heart)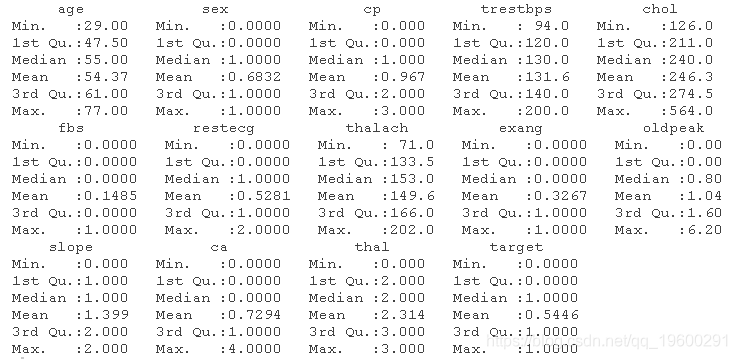
随时关注您喜欢的主题
通过观察以上的总结,我们可以说以下几点
- 性别不是连续变量,因为根据我们的描述,它可以是男性或女性。因此,我们必须将性别这个变量名称从整数转换为因子。
- cp不能成为连续变量,因为它是胸痛的类型。由于它是胸痛的类型,我们必须将变量cp转换为因子。
- fbs不能是连续变量或整数,因为它显示血糖水平是否低于120mg/dl。
- restecg是因子,因为它是心电图结果的类型。它不能是整数。所以,我们要把它转换为因子和标签。
- 根据数据集的描述,exang应该是因子。心绞痛发生或不发生。因此,将该变量转换为因子。
- 斜率不能是整数,因为它是在心电图中观察到的斜率类型。因此,我们将变量转换为因子。
- 根据数据集的描述,ca不是整数。因此,我们要将该变量转换为因子。
- thal不是整数,因为它是地中海贫血的类型。因此,我们将变量转换为因子。
- 目标是预测变量,告诉我们这个人是否有心脏病。因此,我们将该变量转换为因子,并为其贴上标签。
根据上述考虑,我们对变量做了一些变化
#例如
sex<-as.factor(sex)
levels(sex)<-c("Female","Male")检查上述变化是否执行成功
str(heart)
summary(heart)
EDA
EDA是探索性数据分析(Exploratory Data Analysis)的缩写,它是一种数据分析的方法/哲学,采用各种技术(主要是图形技术)来深入了解数据集。
对于图形表示,我们需要库 “ggplot2”
library(ggplot2)
ggplot(heart,aes(x=age,fill=target,color=target)) + geom_histogram(binwidth = 1,color="black") + labs(x = "Age",y = "Frequency", title = "Heart Disease w.r.t. Age")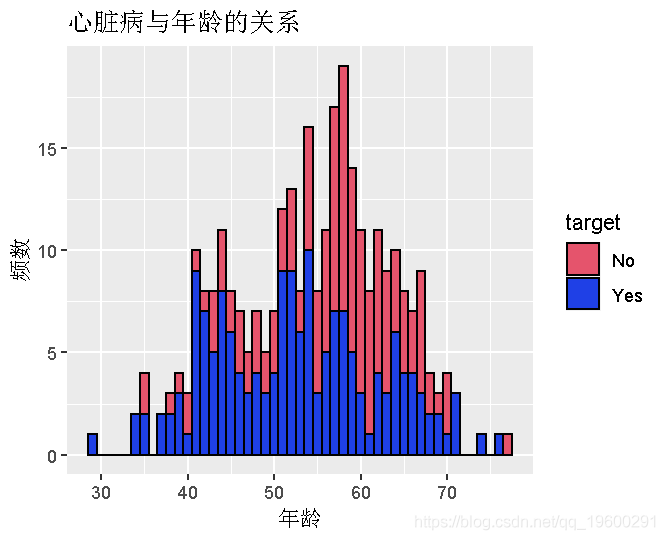
我们可以得出结论,与60岁以上的人相比,40至60岁的人患心脏病的概率最高。
table <- table(cp)
pie(table)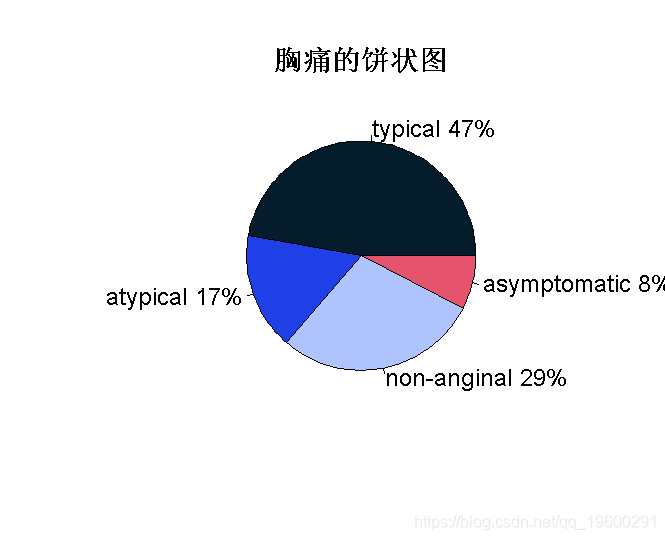
我们可以得出结论,在所有类型的胸痛中,在个人身上观察到的大多数是典型的胸痛类型,然后是非心绞痛。
首先,我们将数据集分为训练数据(75%)和测试数据(25%)。
执行机器学习算法
Logistic回归
set.seed(100)
#100用于控制抽样的permutation为100.
index<-sample(nrow(heart),0.75*nrow(heart))在训练数据上生成模型,然后用测试数据验证模型。
glm(family = "binomial")
# family = " 二项式 "意味着只包含两个结果。为了检查我们的模型是如何生成的,我们需要计算预测分数和建立混淆矩阵来了解模型的准确性。
pred<-fitted(blr)
# 拟合只能用于获得生成模型的数据的预测分数。
我们可以看到,预测的分数是患心脏病的概率。但我们必须找到一个适当的分界点,从这个分界点可以很容易地区分是否患有心脏病。
为此,我们需要ROC曲线,这是一个显示分类模型在所有分类阈值下的性能的图形。它将使我们能够采取适当的临界值。
pred<-prediction(train$pred,train$target)
perf<-performance(pred,"tpr","fpr")
plot(perf,colorize = T,print.cutoffs.at = seq(0.1,by = 0.1))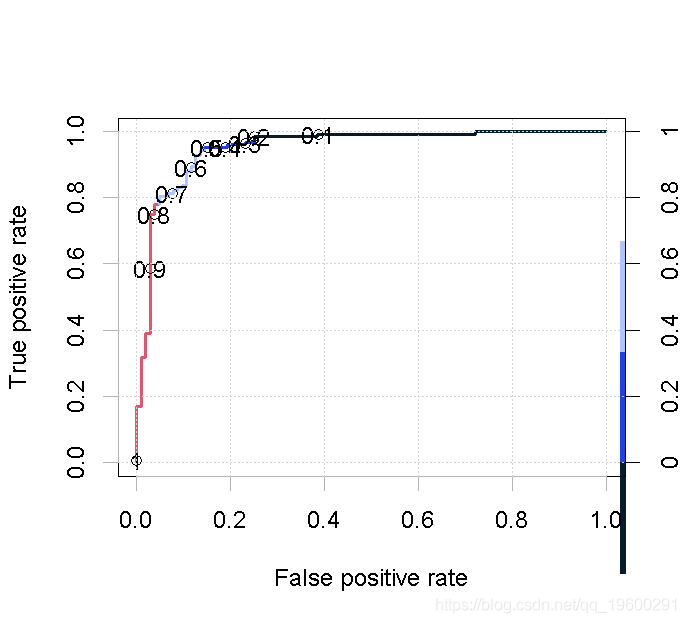
通过使用ROC曲线,我们可以观察到0.6具有更好的敏感性和特异性,因此我们选择0.6作为区分的分界点。
pred1<-ifelse(pred<0.6,"No","Yes")
# 训练数据的准确性
acc_tr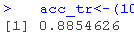
从训练数据的混淆矩阵中,我们知道模型有88.55%的准确性。
现在在测试数据上验证该模型
predict(type = "response")
## type = "response "是用来获得患有心脏病的概率的结果。
head(test)
我们知道,对于训练数据来说,临界点是0.6。同样地,测试数据也会有相同的临界点。
confusionMatrix((pred1),target)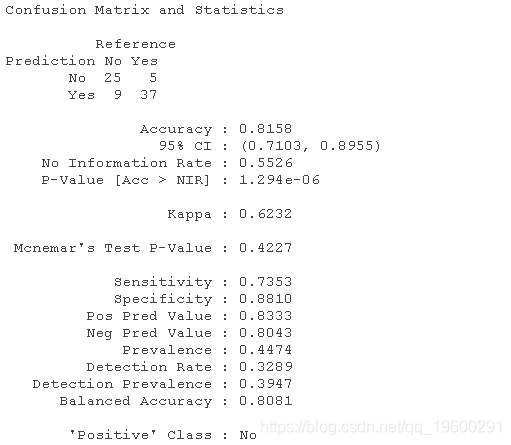
#测试数据的准确性.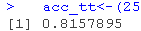
检查我们的预测值有多少位于曲线内
auc@y.values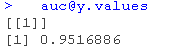
我们可以得出结论,我们的准确率为81.58%,90.26%的预测值位于曲线之下。同时,我们的错误分类率为18.42%。
Naive Bayes算法
在执行Naive Bayes算法之前,需要删除我们在执行BLR时添加的额外预测列。
#naivebayes模型
nB(target~.)用训练数据检查模型,并创建其混淆矩阵,来了解模型的准确程度。
predict(train)
confMat(pred,target)
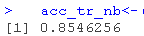
我们可以说,贝叶斯算法对训练数据的准确率为85.46%。
现在,通过预测和创建混淆矩阵来验证测试数据的模型。
Matrix(pred,target)
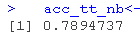
我们可以得出结论,在Naive Bayes算法的帮助下生成的模型准确率为78.95%,或者我们也可以说Naive Bayes算法的错误分类率为21.05%。
决策树
在实施决策树之前,我们需要删除我们在执行Naive Bayes算法时添加的额外列。
train$pred<-NULLrpart代表递归分区和回归树
当自变量和因变量都是连续的或分类的时候,就会用到rpart。
rpart会自动检测是否要根据因变量进行回归或分类。
实施决策树
plot(tree)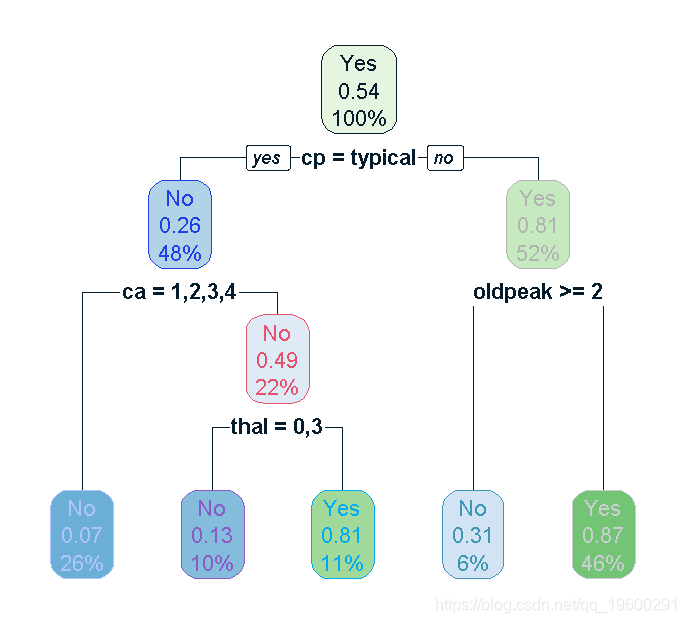
在决策树的帮助下,我们可以说所有变量中最重要的是CP、CA、THAL、Oldpeak。
让我们用测试数据来验证这个模型,并找出模型的准确性。
conMat(pred,targ)
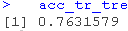
我们可以说,决策树的准确率为76.32%,或者说它的错误分类率为23.68%。
随机森林
在执行随机森林之前,我们需要删除我们在执行决策树时添加的额外预测列。
test$pred<-NULL在随机森林中,我们不需要将数据分成训练数据和测试数据,我们直接在整个数据上生成模型。为了生成模型,我们需要使用随机森林库
# Set.seed通过限制permutation来控制随机性。
set.seed(100)
model_rf<-randomForest(target~.,data = heart)
model_rf
在图上绘制出随机森林与误差的关系。
plot(model_rf)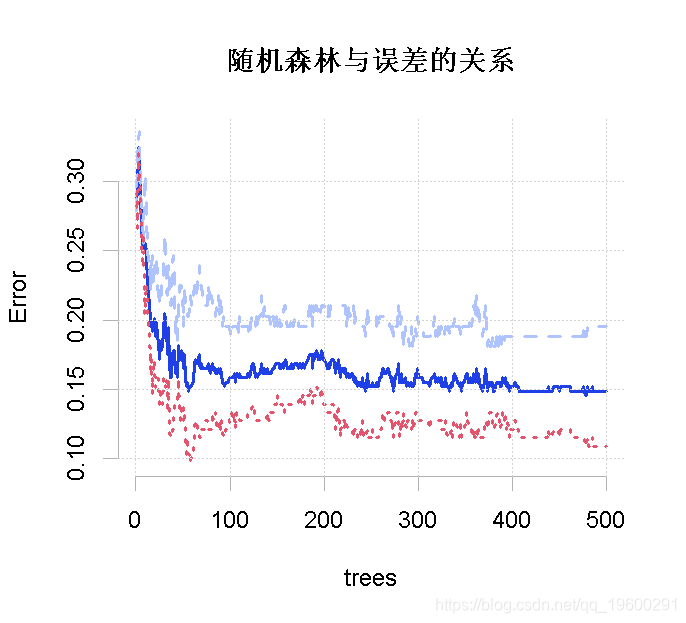
红线代表没有心脏病的MCR,绿线代表有心脏病的MCR,黑线代表总体MCR或OOB误差。总体误差率是我们感兴趣的,结果不错。
结论
在进行了各种分类技术并考虑到它们的准确性后,我们可以得出结论,所有模型的准确性都在76%到84%之间。其中,随机森林的准确率略高,为83.5%。
关于分析师
Xinyao Yi是拓端研究室(TRL)的研究员。在此对她对本文所作的贡献表示诚挚感谢,她在UC San Diego完成了 计算机社会科学专业的硕士学位,专注数据处理、统计建模、机器学习领域。擅长R语言、Python、SQL、SPSS、Stata。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!





 MATLAB奥运会奖牌预测研究 —CNN神经网络、逻辑回归、Liang-Kleeman信息流、多元回归及随机森林模型的因果关联与概率预测|附代码数据
MATLAB奥运会奖牌预测研究 —CNN神经网络、逻辑回归、Liang-Kleeman信息流、多元回归及随机森林模型的因果关联与概率预测|附代码数据 【视频讲解】R语言海七鳃鳗性别比分析:JAGS贝叶斯分层逻辑回归MCMC采样模型应用
【视频讲解】R语言海七鳃鳗性别比分析:JAGS贝叶斯分层逻辑回归MCMC采样模型应用 Python预测二型糖尿病:逻辑回归、XGBoost、CNN、随机森林及BP神经网络融合加权线性回归细化变量及PCA降维创新
Python预测二型糖尿病:逻辑回归、XGBoost、CNN、随机森林及BP神经网络融合加权线性回归细化变量及PCA降维创新
