贝叶斯回归分位数在最近的文献中受到广泛关注,本文实现了贝叶斯系数估计和回归分位数(RQ)中的变量选择,带有lasso和自适应lasso惩罚的贝叶斯。
本文还包括总结结果、绘制路径图、后验直方图、自相关图和绘制分位数图的进一步建模功能。
最近我们被客户要求撰写关于分位数回归的研究报告。回归分位数(RQ)由(Koenker和Gilbert,1978)提出,将感兴趣的结果的条件分位数作为预测因子的函数来建模。
这种方法的主要目的是将感兴趣的结果的条件分位数建模为预测因子的函数。
在传统的回归分析中,我们通常关注因变量的条件均值如何随自变量变化,但在某些情况下,了解因变量的条件分布的其他部分(如中位数或特定的分位数)可能同样重要。
贝叶斯分位数回归是一种统计方法。它结合了贝叶斯理论和分位数回归技术。分位数回归可以估计因变量在不同分位数下与自变量的关系,而贝叶斯方法则通过引入先验分布,利用后验分布进行推断。贝叶斯分位数回归可以处理复杂的数据结构和不确定性,提供更加灵活和稳健的估计结果。它在经济学、金融学、医学等领域有广泛的应用,例如用于分析收入分布、风险评估、生存分析等问题。
自引入以来,分位数回归一直是理论界非常关注的话题,也在许多研究领域得到了大量的应用,如计量经济学、市场营销、医学、生态学和生存分析(Neelon等,2015;Davino等,2013;Hao和Naiman,2007)。
简介
假设我们有一个观察样本{(xi , yi);i = 1, 2, – -, n},其中yi表示因变量,xi表示协变量的k维矢量。
贝叶斯_分位数_回归
Tobit RQ为描述非负因变量和协变量向量之间的关系提供了一种方法,可以被表述为因变量的数据未被完全观察到的分位数回归模型。关于Tobit 分位数回归模型有相当多的文献,我们可以参考Powell(1986)、Portnoy(2003)、Portnoy和Lin(2010)以及Kozumi和Kobayashi(2011)来了解概况。考虑一下这个模型。

其中,yi是观察到的因变量,y∗i是相应的潜在的未观察到的因变量,y 0是一个已知的点。可以证明,RQ系数向量β可以通过以下最小化问题的解来持续估计
Yu和Stander(2007)提出了一种Tobit RQ的贝叶斯方法,使用ALD计算误差,并使用Metropolis-Hastings(MH)方法从其后验分布中抽取β。
真实数据实例
我们考虑用真实的数据例子。
免疫球蛋白G数据
这个数据集包括298名6个月到6岁儿童的免疫球蛋白G的血清浓度(克/升),Isaacs等人(1983)对其进行了详细讨论,Yu等人(2003)也使用了该数据集。为了说明问题,该数据集的贝叶斯分位数回归模型(可以拟合如下)。
rq(血清浓度~年龄, tau=0.5, runs=2000)摘要函数提供估计值和95%的置信区间

绘制数据,然后将五条拟合的RQ线叠加在散点图上。
R> for (i in 1:5) {
+ taus=c(0.05, 0.25, 0.5, 0.75, 0.95)
+ rq(tau=taus[i],runs=500, burn=100)
+ abline(fit, col=i)
+ }
R>
R> for (i in 1:5) {
+ taus=c(0.05, 0.25, 0.5, 0.75, 0.95)
+ fit = rq(tau=taus[i],runs=500, burn=100)
+ curve(,add=TRUE)
+ }
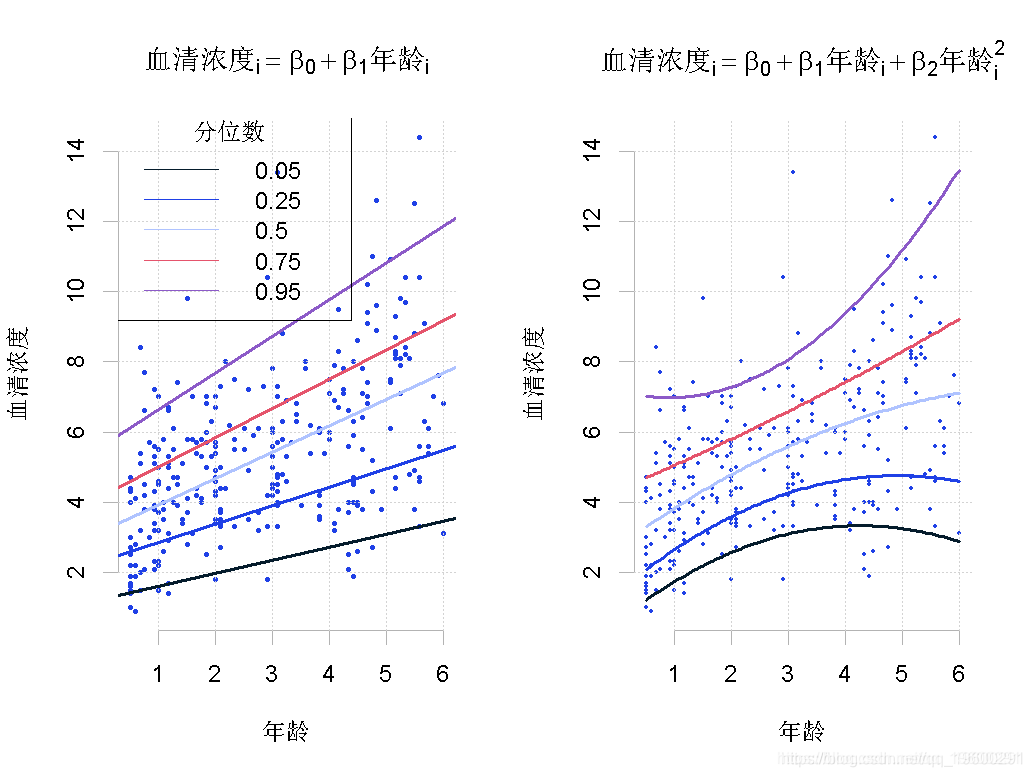
图2:免疫球蛋白G数据的散点图和RQ拟合。
该图显示了298名6个月至6岁儿童的免疫球蛋白G的散点图。叠加在该图上的是{.05, .25, .50, .75, .95}的RQ线(左图)和 RQ线(左图)和RQ曲线(右图)。
图可以用来评估吉布斯采样向平稳分布的收敛情况。我们在图1中只报告了τ=0.50时每个参数的路径图和后验直方图。我们使用以下代码
plot(fit,"tracehist",D=c(1,2))可以通过生成路径图、后验直方图、自相关图来对Gibbs采样的绘制结果进行图形总结。路径和直方图,路径和自相关,直方图和自相关,以及路径、直方图和自相关。这个函数还有一个选项。在图3中,免疫球蛋白G数据系数的路径图表明,采样从后验空间的一个偏远区域跳到另一个区域的步骤相对较少。此外,直方图显示边际密度实际上是所期望的平稳的单变量常态。
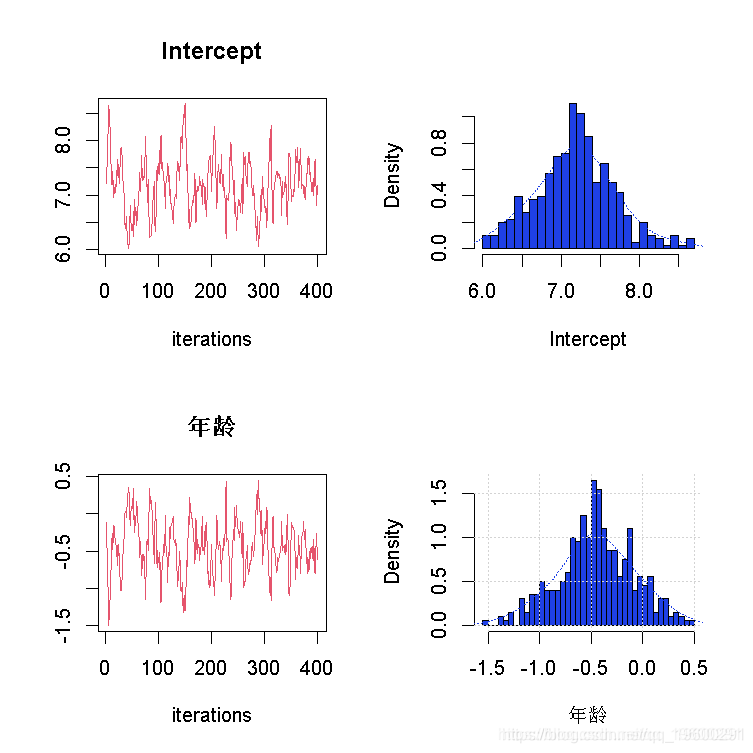
图3:当τ=0.50时,免疫球蛋白G数据集的系数的路径和密度图。

想了解更多关于模型定制、咨询辅导的信息?
前列腺癌数据
在本小节中,我们说明贝叶斯分位数回归在前列腺癌数据集(Stamey等人,1989)上的表现。该数据集调查了等待根治性前列腺切除术的病人的前列腺特异性抗原(lpsa)水平和八个协变量之间的关系。
随时关注您喜欢的主题
这些协变量是:癌症对数体积(lcavol)、前列腺的对数重量(lweight)、年龄(age)、良性前列腺的对数体积(lbph)、精囊侵犯(svi)、胶囊穿透的对数(lcp)、格里森评分(gleason)以及格里森评分4或5的百分比(pgg45)。
在本小节中,我们假设因变量(lpsa)均值为零,而预测因子已被标准化,均值为零。为了说明问题,我们考虑当τ=0.50时,贝叶斯lasso套索RQ(方法=”BLqr”)。在这种情况下,我们使用以下代码
R> x=as.matrix(x)
R> rq(y~x,tau = 0.5, method="BLqr", runs = 5000, burn = 1000, thin = 1)
模型法可用于确定回归中的活跃变量。

相应的吉布斯采样的收敛性是通过生成样本的路径图和边际后验直方图评估的。因此,图可以用来提供一个关于吉布斯采样器收敛的图形检查,通过使用以下代码检查路径图和边际后验直方图。
plot(fit, plottype="trace", D=1:9)
plot(fit, plottype="hist", D=1:9)上述代码的结果分别显示在图4和图5中。图4中的路径图显示,生成的样本迅速穿越了后验空间,图5中的边际后验直方图显示,条件后验分布实际上是所需的平稳单变量常态。
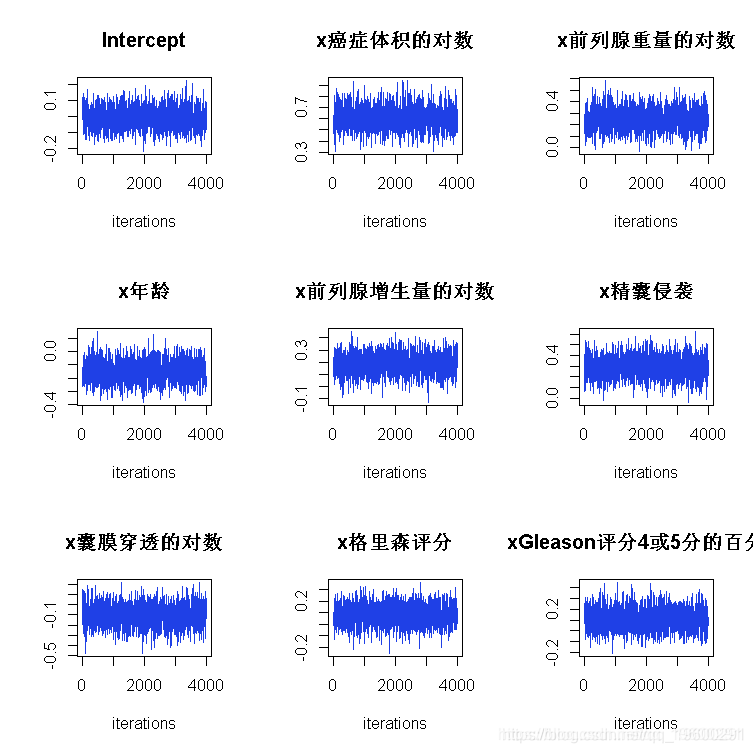
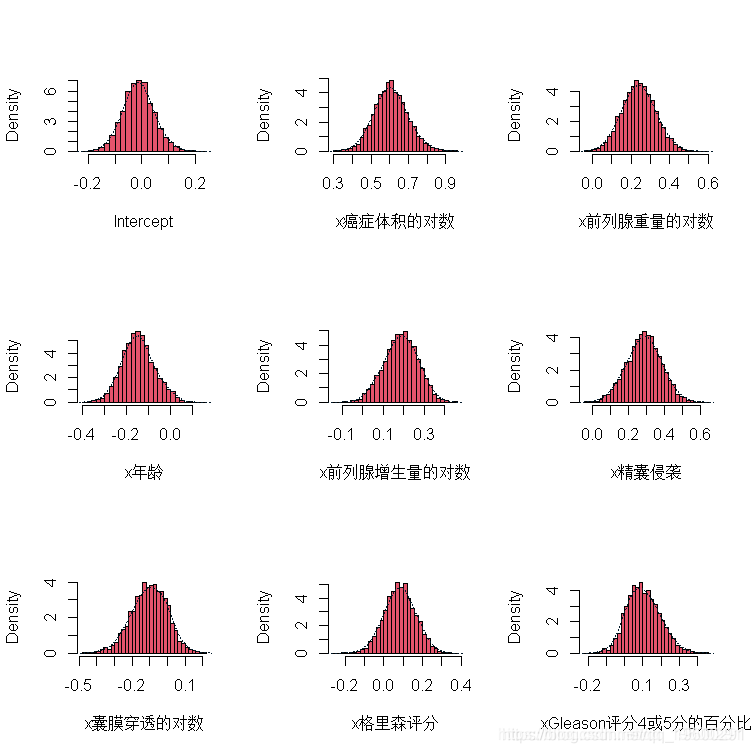
小麦数据
我们考虑一个小麦数据集。这个数据集来自于国家小麦种植发展计划(2017)。这个小麦数据由11个变量的584个观测值组成。因变量是每2500平方米小麦产量增加的百分比。协变量是化肥尿素(U)、小麦种子播种日期(Ds)、小麦种子播种量(Qs)、激光平田技术(LT)、复合肥施肥(NPK)、播种机技术(SMT)、绿豆作物种植(SC)、作物除草剂(H)、作物高钾肥(K)、微量元素肥料(ME)。
下面的命令给出了τ=0.50时Tobit RQ的后验分布。
rq(y~x,tau=0.5, methods="Btqr")
还可以拟合贝叶斯lassoTobit 分位数回归和贝叶斯自适应lassoTobit 分位数回归。当τ=0.50时,函数可以用来获得Tobit 分位数回归的后验平均值和95%的置信区间。

结论
在本文中,我们已经说明了在分位数回归(RQ)中进行贝叶斯系数估计和变量选择。此外,本文还实现了带有lasso和自适应lasso惩罚的贝叶斯Tobit 分位数回归。还包括总结结果、绘制路径图、后验直方图、自相关图和绘制定量图的进一步建模。
参考文献
Alhamzawi, R., K. Yu, and D. F. Benoit (2012). Bayesian adaptive lasso quantile regression. Statistical Modelling 12 (3), 279–297.
Brownlee, K. A. (1965). Statistical theory and methodology in science and engineering, Volume 150. Wiley New York.
Davino, C., M. Furno, and D. Vistocco (2013). Quantile regression: theory and applications. John Wiley & Sons.
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!



 视频讲解|核密度估计朴素贝叶斯:业务数据分类—从理论到实践
视频讲解|核密度估计朴素贝叶斯:业务数据分类—从理论到实践 MATLAB贝叶斯超参数优化LSTM预测设备寿命应用——以航空发动机退化数据为例
MATLAB贝叶斯超参数优化LSTM预测设备寿命应用——以航空发动机退化数据为例 Python谷歌商店Google Play APP评分预测:LASSO、多元线性回归、岭回归模型对比研究
Python谷歌商店Google Play APP评分预测:LASSO、多元线性回归、岭回归模型对比研究 Python糖尿病预测融合模型构建:伯努利朴素贝叶斯、逻辑回归、决策树、随机森林、支持向量机SVM应用
Python糖尿病预测融合模型构建:伯努利朴素贝叶斯、逻辑回归、决策树、随机森林、支持向量机SVM应用
