我想研究如何使用pymc3在贝叶斯框架内进行线性回归。

由Kaizong Ye，Coin Ge撰写

根据从数据中学到的知识进行推断。

可下载资源

贝叶斯规则是什么？

本质上，我们必须将已经知道的知识与世界上的事实相结合。

假设存在这种罕见疾病，每10,000人中就有1人随机感染这种疾病。换句话说，有0.01％的机会患上这种疾病。幸运的是，有一项测试可以99％的正确识别出患有这种疾病的人，如果没有这种疾病，它也可以正确地说出您99％没有患这种疾病。您参加了测试，结果为阳性。您有多少几率实际患上该病？

好吧，让我们从逻辑上考虑一下。我们知道，每10,000人中就有1人患此病。假设有10,000人。他们中的9,999人没有疾病，但其中1％的人会得到阳性结果。因此，即使只有1人实际患有这种疾病，也有约101人获得了阳性结果。这意味着即使结果为阳性，您也只有101分之一的几率实际患上该病（或大约1％的几率）。

如果要将极大似然估计应用到线性回归模型中，模型的复杂度会被两个因素所控制：基函数的数目（ $\theta$ 的维数）和样本的数目。尽管为对数极大似然估计加上一个正则项（或者是参数的先验分布），在一定程度上可以限制模型的复杂度，防止过拟合，但基函数的选择对模型的性能仍然起着决定性的作用。

上面说了那么大一段，就是想说明一个问题：由于极大似然估计总是会使得模型过于的复杂以至于产生过拟合的现象，所以单纯的使用极大似然估计并不是特别的有效。

当然，交叉验证是一种有效的限制模型复杂度，防止过拟合的方法，但是交叉验证需要将数据分为训练集合测试集，对数据样本的浪费也是非常的严重的。

贝叶斯回归

基于上面的讨论，这里就可以引出本文的核心内容：贝叶斯线性回归。

贝叶斯线性回归不仅可以解决极大似然估计中存在的过拟合的问题。
它对数据样本的利用率是100%，仅仅使用训练样本就可以有效而准确的确定模型的复杂度。

在极大似然估计线性回归中我们把参数 $w$ 看成是一个未知的固定值，而贝叶斯学派则把 $w$ 看成是一个随机变量。

线性回归模型是一组输入变量 $x$ 的基函数的线性组合，在数学上其形式如下：

$y(x,w)=w_{0}+\sum_{j=1}^{M}\omega_{j}\phi_{j}(x)$

这里 $\phi_{j}(x)$ 就是前面提到的基函数，总共的基函数的数目为 $M$ 个，如果定义 $\phi_{0}(x)=1$ 的话，那个上面的式子就可以简单的表示为：

$y(x,w)=\sum_{j=0}^{M}\omega_{j}\phi_{j}(x)=w^T\phi(x)$

$w=(w_{0},w_{1},w_{2},...,w_{M})$

$\phi=(\phi_{0},\phi_{1},\phi_{2},...,\phi_{M})$

以下 $t$ 是 $x$ 对应的目标输出，即样本为 $(x,t)$ ，并且假设样本集合满足正态分布，参数 $w$ 也满足正态分布， $\alpha^{-1}$ 和 $\beta^{-1}$ 分别对应于 $w$ 与样本集合的高斯分布方差。

则参数 $\w$ $w$ 满足以下分布：

$p(w)=N(w|0,\alpha^{-1}I)$

线性模型的概率表示如下：

$p(t|x,w,\beta)=N(t|y(x,w),\beta^{-1}I)$

参数有点多。 $p(t|x,w,\beta)$ 表示样本 $(x,t)$ 的输出 $t$ 关于输入特征 $x$ 、模型参数 $w$ 以及样本分布方差 $\beta$ 的概率密度函数。其服从于 $N(t|y(x,w),\beta^{-1}I)$ 正态分布，这个正态分布在线性回归的概率解释中出现过，表示均值为 $y(x,w)$ ，方差为 $\beta^{-1}I$ 的正态分布（ $I表示单位矩阵$ ），可以通过残差的独立正态分布性质推导得到。

一般来说，我们称 $p(w)$ 为共轭先验(conjugate prior)。

在贝叶斯统计中，如果后验分布与先验分布属于同类，则先验分布与后验分布被称为共轭分布，而先验分布被称为似然函数的共轭先验。

共轭先验的好处主要在于代数上的方便性，可以直接给出后验分布的封闭形式，否则的话只能数值计算。共轭先验也有助于获得关于似然函数如何更新先验分布的直观印象。

那么，线性模型的后验概率函数： $L(\theta)=L(w)$ 下面笔误。

且注意，到这一步之后与最大似然估计其实一模一样了，最大后验估计与最大似然估计的唯一区别就在于是否加上先验也就是这里的 $p(w)$ ，乘上 $p(w)$ 之后不必再纠结在 $p(t_i|x_i,w,\beta^{-1}I)$ 中 $w$ 为随机变量，此时的 $w$ 完全可以理解为MLE中的待估参数，在先验 $p(w)$ 给定下是已经确定了的，只是我们还不知道。

$L(\theta) & =\prod _{i=1}^mp(t_i|x_i,w,\beta^{-1}I)p(w)\\\\ & = \prod _{i=1}^mp(t_i|x_i,w,\beta^{-1}I) \prod _{j=1}^np(w^{(j)})\\\\ &=\prod _{i=1}^m\sqrt{\beta\over2\pi}\ \exp({-\beta\left [ t_i-y(x_i,w)\right ]^2\over2})\prod _{j=1}^n\sqrt{\alpha\over2\pi}\ \exp({-\alpha\left [ w^{(j)} \right ]^2\over2})$

对数后验概率函数为：

$\ell(w)=ln L(w) & = ln\left [ \prod _{i=1}^mp(t_i|x_i,w,\beta^{-1}I) \prod _{j=1}^np(w^{(j)}) \right ]\\\\ &=ln\left [ \prod _{i=1}^m\sqrt{\beta\over2\pi}\ \exp({-\beta\left [ t_i-y(x_i,w)\right ]^2\over2})\prod _{j=1}^n\sqrt{\alpha\over2\pi}\ \exp({-\alpha\left [ w^{(j)} \right ]^2\over2}) \right ]\\\\ &= \sum _{i=1}^m \left [ {1\over2}ln{\beta\over2\pi}-{\beta\left [ t_i-y(x_i,w)\right ]^2\over2} \right ]+ \sum _{j=1}^n\left [ {1\over2}ln{\alpha\over2\pi} -{\alpha\left [ w^{(j)} \right ]^2\over2} \right ]\\\\ &={m\over2}ln{\beta\over2\pi}+{n\over2}ln{\alpha\over2\pi} - {\beta\over2}\sum _{i=1}^m{\left [ t_i-y(x_i,w)\right ]^2\over2}-{\alpha\over2}w^Tw$

最后我们可以化为：

$\ell(w)=-{\beta\over2}\sum _{i=1}^m{\left [ t_i-y(x_i,w) \right ]^2\over2}-{\alpha\over2}w^Tw+const$

$\max_w \ell(w)\ \ <=>\ \ \min_w {\beta\over2}\sum _{i=1}^m{\left [ t_i-y(x_i,w) \right ]^2\over2}+{\alpha\over2}w^Tw$

这不就是加了L2正则的loss function吗，于是我们就利用贝叶斯估计准确来讲是最大后验估计加上高斯先验推导出了带有L2正则的线性回归！

这里可以看出，先验概率对应的就是正则项，其正则参数为 $\lambda=\alpha/\beta$ 。

可以假设，复杂的模型有较小的先验概率，而相对简单的模型有较大的先验概率。

数学描述：

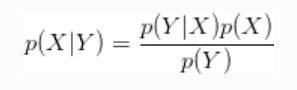
看起来很简单。实际上，这很简单。该公式仅需要一些概率分布的知识。但是实际上，右边的分母通常意味着我们将要计算很多真正的计算重积分。因此，贝叶斯统计被放弃了很多年。从某种意义上讲，它自然而然地脱离了概率论。如果我们只有擅长计算大量数字的东西，那么这类问题就可以解决。

计算机确实非常快地进行计算贝叶斯回归。

视频

贝叶斯推断线性回归与R语言预测工人工资数据

探索见解 ➜

去bilibili观看 ➜

探索更多视频 ➜

代码

这是进行贝叶斯回归所需的知识。通常，我们想到这样的回归：

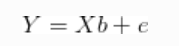
e是正态分布的误差。

因此，我们假设：

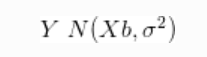
与先验：

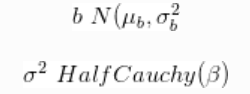
因此，如果我们拥有X和Y的数据，则可以进行贝叶斯线性回归。

代码

因此，我们要使用的数据集是《美国住房调查： 2013年住房负担能力数据》数据集。

我们感兴趣的是住房负担如何随着年龄而变化。AGE1包含户主的年龄。BURDEN是一个变量，它告诉我们住房费用相对于收入有多大。为简单起见，我们仅关注这两个变量。我们想知道的是，随着年龄的增长，住房负担会变得更容易吗？特别是，我们想知道斜率系数是否为负，并且由于我们处于贝叶斯框架中，因此该概率为负的概率是多少？

因此，我们将导入所需的库和数据。进行一些数据清理。


df=pd.read_csv('2013n.txt',sep=',')
df=df[df['BURDEN']>0]
df=df[df['AGE1']>0]

现在，让我们构建上面讨论的模型。让我们做一个散点图，看看数据是什么样子。

最受欢迎的见解

1.matlab使用贝叶斯优化的深度学习

2.matlab贝叶斯隐马尔可夫hmm模型实现

3.R语言Gibbs抽样的贝叶斯简单线性回归仿真

4.R语言中的block Gibbs吉布斯采样贝叶斯多元线性回归

5.R语言中的Stan概率编程MCMC采样的贝叶斯模型

6.Python用PyMC3实现贝叶斯线性回归模型

7.R语言使用贝叶斯层次模型进行空间数据分析

8.R语言随机搜索变量选择SSVS估计贝叶斯向量自回归（BVAR）模型

9.matlab贝叶斯隐马尔可夫hmm模型实现

plt.scatter(df['AGE1'],df['BURDEN'])
plt.show()

结果如下：

R语言中的block Gibbs吉布斯采样贝叶斯多元线性回归

阅读文章 ➜

数据看起来住房负担天文数字很高，很容易超过收入的10倍。

现在，我们不必为此担心太多。这是构建和运行模型的代码：


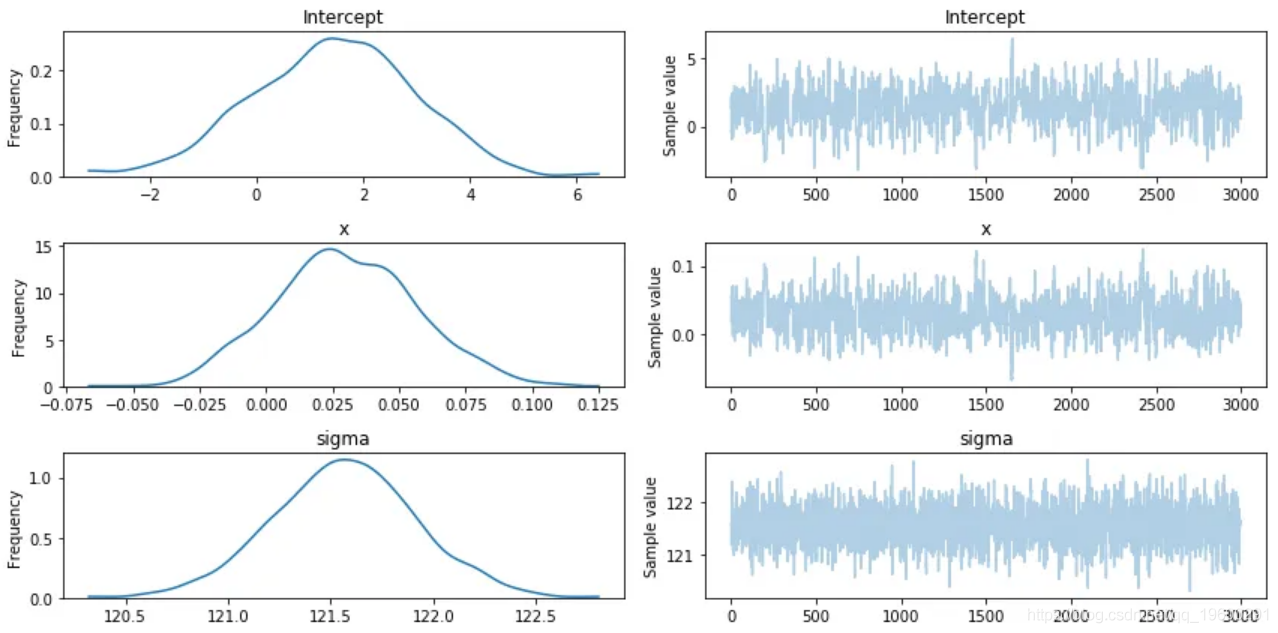
pm.traceplot(trace)
plt.show()

看起来与我们上面的模型完全一样，不同之处在于我们还有一个正态分布的截距beta。现在我们的模型已经训练好了，我们可以继续做一些推论工作。

完成运行后，会看到类似以下内容：

随时关注您喜欢的主题

可以看到，我们有斜率和截距的后验分布以及回归的标准偏差。

住房负担会随着年龄的增长而减少吗？

是的。随着人们的建立，他们的住房成本将相对于收入下降。这将等于年龄变量的负斜率系数。运行以下代码，则可以找出斜率系数为负的确切概率。

print(np.mean([1 if obj<0 else 0 for obj in trace['x']]))

该系数为负的概率约为13.8％。

可下载资源

关于作者

Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。

本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。

非常感谢您阅读本文，如需帮助请联系我们！

Python贝叶斯回归分析住房负担能力数据集

贝叶斯规则是什么？

贝叶斯回归

代码

代码

R语言中的block Gibbs吉布斯采样贝叶斯多元线性回归

数据看起来住房负担天文数字很高，很容易超过收入的10倍。

随时关注您喜欢的主题

相关文章

Python贝叶斯回归分析住房负担能力数据集

贝叶斯规则是什么？

贝叶斯回归

代码

代码

R语言中的block Gibbs吉布斯采样贝叶斯多元线性回归

数据看起来住房负担天文数字很高，很容易超过收入的10倍。

随时关注您喜欢的主题

相关文章

关注有关新文章的微信公众号