R语言Wald检验 vs 似然比检验

By tecdat9月 18, 2019大数据部落, 数理统计, 计算机科学与技术R语言, Wald检验, 似然比检验, 检验

在开展基于概率推理的课程时，关键主题之一是基于似然函数的检验和置信区间构建。

由Kaizong Ye，Coin Ge撰写

通常包括Wald，似然比和分数检验。在这篇文章中，我将修改Wald和似然比检验的优缺点。

可下载资源

完整程序、数据和文档（word）

我将重点关注置信区间而不是检验。

×

求MLE的方法

1）一般方法

求总样本的似然函数 $p(x;\theta )$ ，也可以进一步表示成对数似然形式 $lnp(x;\theta )$ ；然后对对数似然PDF求估计参数的偏导 $\frac{\partial lnp(x;\theta )}{\partial \theta }$ ，并令其等于零来求取MLE估计 $\hat{\theta }$ 。注意：若这样求取的 $\hat{\theta }$ 不再 $\theta$ 范围内时，那么在 $\theta$ 的允许范围区间取找 $\hat{\theta }$ 使 $p(x;\theta )$ 或者 $lnp(x;\theta )$ 最大即可。

2）特殊方法（一般用于无法直接求解 $\frac{\partial lnp(x;\theta )}{\partial \theta }=0$ 的请况）

i> Newton-Raphson方法（迭代法）

首先令 $g(\theta )=\frac{\partial lnp(x;\theta )}{\partial \theta }$

然后对 $g(\theta )=0$ 的解进行一个初始猜测值 $\theta_{0}$ 。假设 $g(\theta )$ 在 $\theta_{0}$ 附近是近似线性的，则 $g(\theta )$ 近似表示为

$g(\theta )=g(\theta _{0})+\frac{\mathrm{d} g(\theta )}{\mathrm{d} \theta }|_{\theta =\theta _{0}}(\theta -\theta _{0})$

随后由利用这个式子求解零值所对应的 $\theta_{1}$ ， $\theta_{1}$ 为

$\theta _{1}=\theta _{0}-\frac{\mathrm{d} g(\theta )}{\mathrm{d} \theta }|_{\theta =\theta _{0}}$

重复上面过程：用 $\theta_{1}$ 作 $g(\theta )$ 的线性化点，不断求新的零值点。新点的迭代求取公式如下

$\theta _{k+1}=\theta _{k}-\frac{\mathrm{d} g(\theta )}{\mathrm{d} \theta }|_{\theta =\theta _{k}}$

最终将 $g(\theta )$ 带入迭代公式中得到MLE表达

$\theta _{k+1}=\theta _{k}-[\frac{\partial^2 lnp(x;\theta )}{\partial \theta ^2}]^{-1 }\frac{\partial lnp(x;\theta )}{\partial \theta }|_{\theta =\theta _{k}}$

Remark：迭代可能不收敛；即使迭代收敛，求得的值可能不是全局最大的（解决方法：最好采取多个起始点迭代）。

ii> 得分法（迭代法）

该方法考虑到MLE是MVU估计量，具有有效性，达到CRLB。则可以近似将N-R迭代法中的二阶导换掉

$\frac{\partial^2 lnp(x;\theta )}{\partial \theta ^2}|_{\theta =\theta _{k}}\approx -I(\theta _{k})$

即最终迭代的MLE表达

$\theta _{k+1}=\theta _{k}+I^{-1}(\theta )\frac{\partial lnp(x;\theta )}{\partial \theta }|_{\theta =\theta _{k}}$

Remmark：存在与N-R迭代法一样的收敛问题。

示例

我们将X表示观察到的成功次数的随机变量，x表示其实现的值。似然函数只是二项式概率函数，但参数是模型参数。所以MLE只是观察到的比例。

Wald置信区间

如果我们使用将参数空间（在我们的示例中为区间（0,1））映射到整个实线的变换，那么我们保证在原始比例上获得仅包括允许参数值的置信区间。

课程

R语言数据分析挖掘必知必会

从数据获取和清理开始，有目的的进行探索性分析与可视化。让数据从生涩的资料，摇身成为有温度的故事。

立即参加 ➜

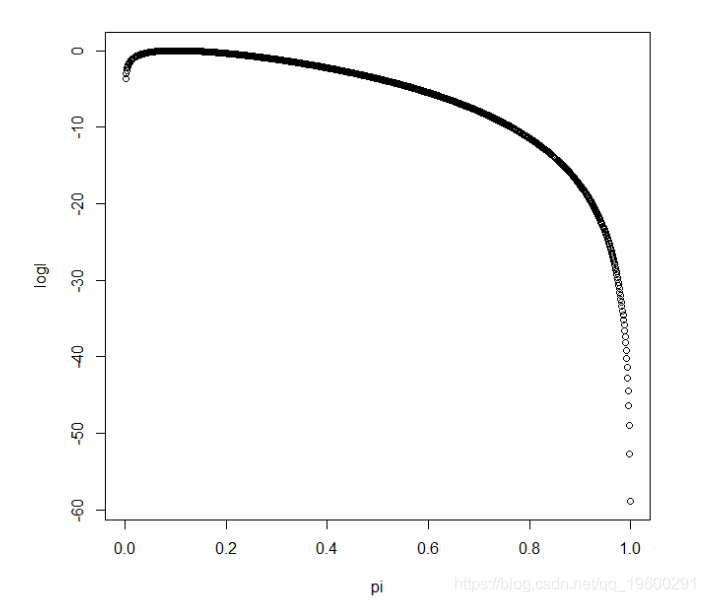
对于概率参数绘制的n = 10，x = 1的二项式示例的对数似然函数：

从视觉上我们可以看出，对数似然函数在绘制时 实际上不是二次方。下图显示了相同的对数似然函数，但现在x轴是对数几率：

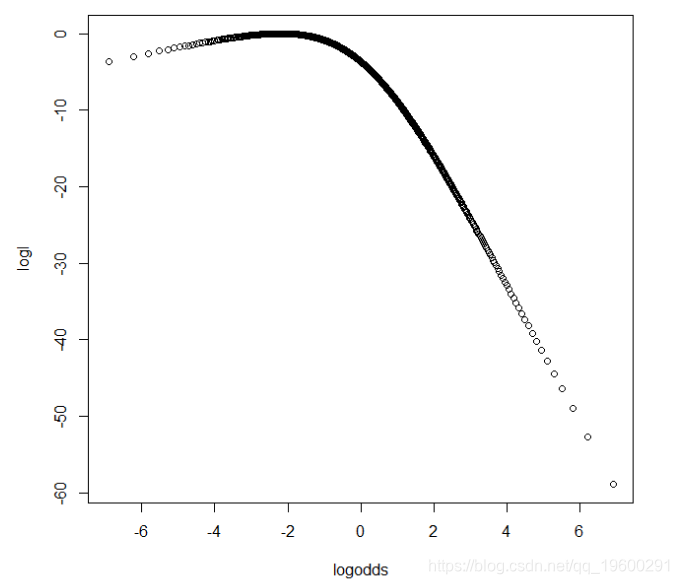
二项式的对数似然函数n = 10 x = 1检验，相对于对数几率。

最受欢迎的见解

1.Matlab马尔可夫链蒙特卡罗法（MCMC）估计随机波动率（SV，Stochastic Volatility）模型

2.基于R语言的疾病制图中自适应核密度估计的阈值选择方法

3.WinBUGS对多元随机波动率模型：贝叶斯估计与模型比较

4.R语言回归中的hosmer-lemeshow拟合优度检验

5.matlab实现MCMC的马尔可夫切换ARMA – GARCH模型估计

6.R语言区间数据回归分析

7.R语言WALD检验 VS 似然比检验

8.python用线性回归预测股票价格

9.R语言如何在生存分析与Cox回归中计算IDI，NRI指标

似然比置信区间

虽然似然比方法具有明显的统计优势，但计算上Wald区间/测试更容易。在实践中，如果样本量不是太小，并且Wald区间是以适当的比例构建的，它们通常是合理的。然而，在小样本中，似然比方法可能是优选的。

可下载资源

关于作者

Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。

本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。

非常感谢您阅读本文，如需帮助请联系我们！

相关文章

售前咨询热线

15121130882

售后咨询热线

0571-63341498