脉冲响应分析是采用向量自回归模型的计量经济学分析中的重要一步。
它们的主要目的是描述模型变量对一个或多个变量的冲击的演化。因此使它们成为评估经济时非常有用的工具。这篇文章介绍了VAR文献中常用的脉冲响应函数的概念和解释。
脉冲响应函数在VAR（向量自回归）模型中是一个核心概念，它描述了模型中一个内生变量受到冲击时，其他内生变量会如何动态地响应这种冲击。这种响应是通过观察模型中的变量在冲击发生后的一段时间内如何变化来衡量的。脉冲响应函数可以被视为一种条件预测或点估计，用于估计冲击发生后不同时间点的变量值。
在VAR模型中，脉冲响应函数不仅关注单一变量的变化，而且能够全面展现多个变量间的相互作用。当模型中的某个变量受到“外生冲击”时，脉冲响应函数能够揭示其他变量如何受到这种冲击的动态影响。通过绘制脉冲响应图形，我们可以直观地观察到这些变量在冲击发生后的动态变化过程。
可下载资源
作者
模型与数据
为了说明脉冲响应函数的概念，使用了Lütkepohl（2007）的示例。可以从教科书的网站上下载所需的数据集。
脉冲响应函数是什么意思?脉冲响应函数经济意义脉冲响应函数描述的是VAR模型中的一个内生变最的冲击给其他内生变且所带来的影响。而方差分解(variancedecomposition)是通过分析每一个结构冲击对内生变l变化(通常用方差来度虽)的贡献度，脉冲响应函数进一步评价不同结构冲击的重要性。因此，脉冲响应函数方差分解给出对VAR模型中的变最产生影响的每个随机扰动的相对重要性的信息。其墓本思想如下所述。
脉冲响应函数是随着时间的推移，脉冲响应函数观察模型中的各变最对于冲击是如何反应的，脉冲响应函数然而对于只是要简单地说明变最间的影响关系又稍稍过细了一些。因此，脉冲响应函数于1980年提出了方差分解方法，定且地把握变量间的影响关系。
它包含从1960年1季度到1982年4季度按季度和季节性调整的时间序列，这些序列是西德的固定投资，可支配收入和数十亿德国马克的消费支出。
# 下载数据
data <- read.table("e1.dat", skip = 6, header = TRUE)
# 仅使用前76个观测值，因此有73个观测值
# 取一阶差分后，留给估计的VAR(2)模型。
data <- data[1:76, ]
# 转换为时间序列对象
data <- ts(data, start = c(1960, 1), frequency = 4)
# 取对数和差值
data <- diff(log(data))
# 绘图数据
plot(data, main = "Dataset E1 from Lütkepohl (2007)")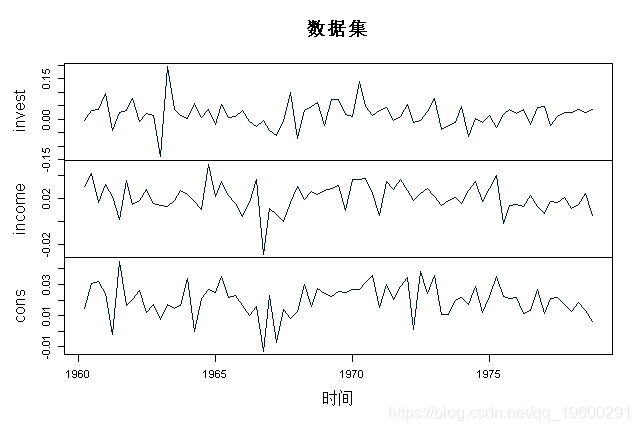
此数据用于估计具有常数项的VAR（2）模型。
估算值
可以使用vars软件包估算VAR模型：
# 查看摘要统计信息
summary(model)代码的结果应与Lütkepohl（2007）的3.2.3节中的结果相同。
预测误差脉冲响应
由于VAR模型中的所有变量都相互依赖，因此单独的系数估计仅提供有关反应的有限信息。为了更好地了解模型的动态行为，使用了脉冲响应（IR）。
线性VAR模型的每个脉冲响应函数的出发点都是其移动平均值（MA）表示，这也是预测误差脉冲响应（FEIR）函数。
在R 中，程序包可用于获取预测误差脉冲响应。
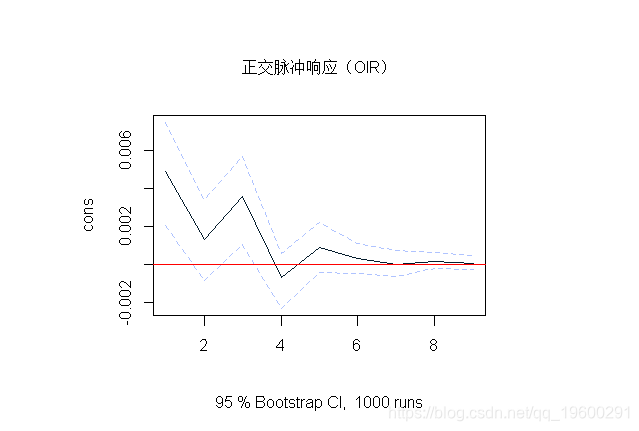
识别问题
从上图可以看出，在第一期间FEIR为零。对于使用的数据集，估计为
## invest income cons
## invest 2.129629e-03 7.161667e-05 1.232404e-04
## income 7.161667e-05 1.373377e-04 6.145867e-05
## cons 1.232404e-04 6.145867e-05 8.920351e-05由于估计方差-协方差矩阵的非对角线元素不为零，因此我们可以假设VAR模型中的变量之间存在同期相关性。这由与Σ相对应的相关矩阵确认：
## invest income cons
## invest 1.0000000 0.1324242 0.2827548
## income 0.1324242 1.0000000 0.5552611
## cons 0.2827548 0.5552611 1.0000000但是，这些矩阵仅描述了误差之间的相关性，但不清楚因果关系的方向。识别这些因果关系是任何VAR分析的主要挑战之一。
正交脉冲响应
识别VAR模型的冲击的常用方法是使用正交脉冲响应（OIR）。基本思想是分解方差-协方差矩阵，使∑ = PP− 1，其中P是带有正对角线元素的下三角矩阵，通常通过Choleski分解获得。给定估计方差-协方差矩阵PP，可以通过以下方法获得分解
## invest income cons
## invest 0.046147903 0.000000000 0.000000000
## income 0.001551894 0.011615909 0.000000000
## cons 0.002670552 0.004934117 0.007597773从这个矩阵可以看出，收入冲击对消费具有同时性的影响，反之则不然。
在R 中，vars可以通过设置参数来使用包的功能来获得OIR：
plot(oir)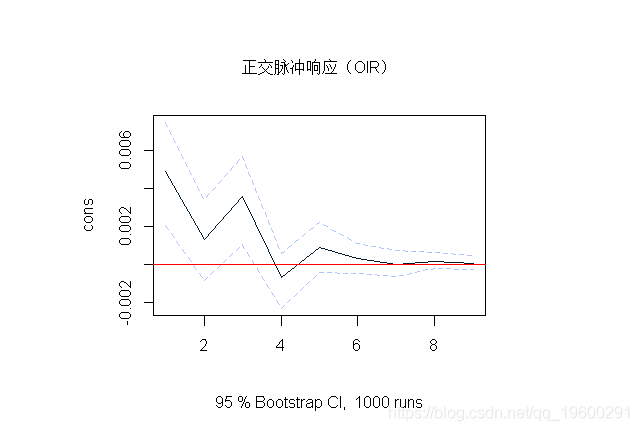
请注意，Choleski分解的输出是一个较低的三角矩阵，因此第一行中的变量永远不会对任何其他变量的同时冲击敏感，而系统中的最后一个变量将对所有其他变量的冲击敏感。因此，OIR的结果可能对变量的顺序很敏感，建议用不同的顺序估计上述VAR模型，以查看所产生的OIR受此影响的程度。
随时关注您喜欢的主题
结构脉冲反应
在VAR模型的估计过程中，结构脉冲响应（SIR）已经考虑了识别问题。
广义脉冲响应
正交和结构响应都可以通过找到变量的正确顺序或通过识别估计的结构参数来约束。Koop等（1998）提出了一种不同类型的响应函数，即所谓的广义脉冲响应（GIR）。它们独立于变量顺序，因为它们将其他冲击的影响整合到响应之外。
对于难以识别结构关系的大型系统，GIR非常有用。
参考文献
Koop, G., Pesaran, M. H., Potter, S. M. (1996). Impulse response analysis in nonlinear multivariate models. Journal of Econometrics 74, 119-147. doi:10.1016/0304-4076(95)01753-4
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
R语言汇率、股价指数与GARCH模型分析：格兰杰因果检验、脉冲响应与预测可视化
【视频】因子分析简介及R语言应用实例：对地区经济研究分析重庆市经济指标
R语言宏观经济学：IS-LM曲线可视化货币市场均衡
R语言代做编程辅导和解答GLM Coursework
