最近我们被客户要求撰写关于波动率的研究报告。
波动率是众多定价和风险模型中的关键参数,例如BS定价方法或风险价值的计算。
在这个模型中,或者说在教科书中,这些模型中的波动率通常被认为是一个常数。
然而,情况并非如此,根据学术研究,波动率是具有聚类,厚尾和长记忆特征的时间序列变量。
本博客比较了GARCH模型(描述波动率聚类),ARFIMA模型( 长记忆),HAR-RV模型(基于高频数据 ),以及来自SSE 50指数和CME利率期货的样本。
此外,本文使用滚动时间窗预测方法来计算预测波动率并构建指数以评估模型的准确性。结果表明,基于长记忆和实现波动率的ARFIMA-RV模型是最准确的模型。
在建议用于预测已实现波动率的模型中,Corsi的HAR-RV在性能和简便性方面均脱颖而出。
“ HAR-RV”代表已实现波动性的异质自回归模型,并且基于所谓的“异质市场假说”。这表明,金融市场是人们以不同的频率行事的相互作用(例如,以高频率运行的公司,日内交易的交易商和低频率的机构投资者)。每一类市场都会以不同的频率引起波动,这将在一定程度上影响彼此。从这些考虑出发,想到了独立但联合地对每个波动频率建模的想法。这使我们得出以下结构非常简单的模型:
RV_d + 1 = b_0 + b_1 * RV_d + b_2 * RV_w + b_3 * RV_m
其中RV_d + 1是第二天的RV,RV_d是前一天的RV,RV_w是前一周的平均日RV,RV_m是前一个月的平均RV。在这种情况下,RV是给定频率下日内收益平方和的平方根。
b_0,b_1,b_2和b_3是要找到的回归参数。
如您所见,该模型基本上是一个简单的回归模型,但是它在性能方面与更复杂的模型(例如ARFIMA)进行了比较。实际上,HAR-RV能够对有关RV的主要程式化事实进行建模,例如自相关和长记忆效应(尽管该模型本身不是长记忆模型,它利用了AR(1)的简单总和的发现这一优势。进程可能显示为长存储进程)。
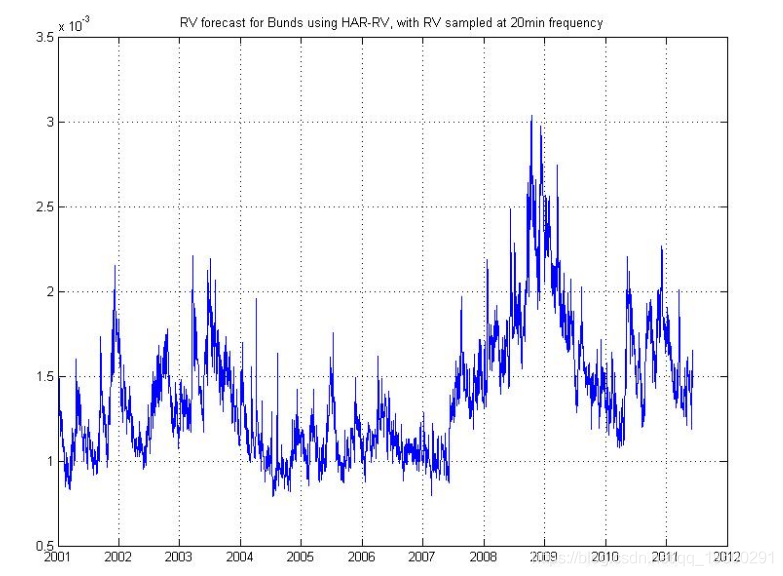
这是预测的已实现波动率的图:
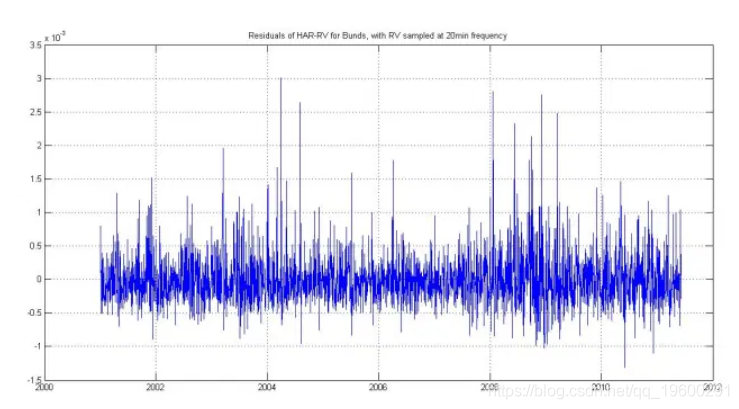
这是实际RV的残差:
基于GARCH的模型
描述波动率聚类
为了模拟异方差性,GARCH采用以下过程:

为了反映金融市场的不对称性,学者们提出了EGARCH,TGARCH或APARCH,其中APARCH更为一般。

我们从在R中拟合APARCH开始:

可以看出ARCH效应是显而易见的
我们通过acf和pacf定义模型阶数

我们可以得到模型的系数,以及误差分析
我们可以查看模型摘要:包含模型系数、误差和显著性等信息。



得到模型的误差分析和标准残差测试。
为了进一步分析模型,我们分析了QQ图中的正态性残差。

我们发现残差不符合正态性,然后我们测试残差的自相关:
测试对于上面列出的模型,所有残差都具有一些自相关效应。因此,基于GARCH的模型可能不够准确,无法预测波动性。
我们使用MSE(误差的均方)来测量模型的预测性能。
| MSE.NGARCH | 0.000385108313676526 |
| MSE.tGARCH | 0.00038568802365854 |
| MSE.APARCH | 0.000385278917823468 |
基于HAR-RV的模型
处理高频实际波动率
高频数据包含更丰富的日内交易信息,因此可用于衡量波动率。实现波动是其中一种方式。
如果我们将交易日t划分为N个时段,每个时段都会有一个对数收益率,那么实际收益可以计算如下:
HAR-RV,异构自回归RV模型由科希创建。






MSE计算如下
| MSE.HARRV | 1.08226110318177 * 10 ^( – 7) |
| MSE.HARRVCJ | 1.90270268315141 * 10 ^( – 7) |
基于ARFIMA的模型
描述长记忆
ARFIMA是分整自回归移动平均模型,其具有与ARMA模型相同的表示形式,但差分参数d可以是非整数值:
随时关注您喜欢的主题

在差分参数d是非整数的情况下,则可以如下操作

在R中,我们编程探索HAR-RV和HAR-RV-CJ模型。



MSE如下所列
| MSE.ARFIMA1 | 1.0663781087345 * 10 ^( – 7) |
| MSE.ARFIMA2 | 1.06634734745652 * 10 ^( – 7) |
| MSE.ARFIMA3 | 1.06846983445809 * 10 ^( – 7) |
结论
| SH50 | S&P500 | |
| MSE.NGARCH | 0.000385108314 | 7.793024760363 * 10 ^( – 5) |
| MSE.tGARCH | 0.000385688024 | 7.803986179542 * 10 ^( – 5) |
| MSE.APARCH | 0.000385278919 | 7.781641356006 * 10 ^( – 5) |
| MSE.HARRV | 1.082261103181 * 10 ^( – 7) | 1.459464289508 * 10 ^( – 9) |
| MSE.HARRVCJ | 1.902702683151 * 10 ^( – 7) | N / A(没有足够的数据) |
| MSE.ARFIMA1 | 1.066378108737 * 10 ^( – 7) | 1.820349558502 * 10 ^( – 8) |
| MSE.ARFIMA2 | 1.066347347457 * 10 ^( – 7) | 1.848206765296 * 10 ^( – 8) |
| MSE.ARFIMA3 | 1.068469834458 * 10 ^( – 7) | 1.844987432992 * 10 ^( – 8) |
从结果我们知道基于ARFIMA的模型具有与HAR-RV相似的准确度,并且两者都比GARCH模型好得多。


 CrewAI与GPT融合多智能体MAS与实时数据预测2026T20世界杯胜者|附代码数据
CrewAI与GPT融合多智能体MAS与实时数据预测2026T20世界杯胜者|附代码数据 llama的Qwen3.5大模型单GPU高效部署与股票筛选应用|附代码教程
llama的Qwen3.5大模型单GPU高效部署与股票筛选应用|附代码教程 Python用Seedream4.5图像生成模型API调用与多场景应用|附代码教程
Python用Seedream4.5图像生成模型API调用与多场景应用|附代码教程 R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据
R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据




1 comment on “R语言预测期货波动率的实现:ARCH与HAR-RV与GARCH,ARFIMA模型比较”