
特别是在经济学/计量经济学中,建模者不相信他们的模型能反映现实。
比如:收益率曲线并不遵循三因素的Nelson-Siegel模型,股票与其相关因素之间的关系并不是线性的,波动率也不遵循Garch(1,1)过程,或者Garch(?,?)。
我们只是试图为我们看到的现象找到一个合适的描述。
模型的发展往往不是由我们的理解决定的,而是由新的数据的到来决定的,这些数据并不适合现有的看法。有些人甚至可以说,现实没有基本的模型(或数据生成过程)。正如汉森在《计量经济学模型选择的挑战》中写道。
1、随机森林是bagging思想和决策树的结合,而GBDT是boosting思想和决策树的结合。其中的bagging思想。bagging的主要思想是训练集是在原始集中有放回选取的,从原始集中选出的各轮训练集之间是独立的;boosting的思想则是每一轮的训练集不变,只是训练集中每个样例在分类器中的权重发生变化。
2、随机森林可以是回归树,也可以是分类树,而GBDT只能由回归树构成。
3、随机森林是并行生成众多决策树模型的,而GBDT是按顺序串行生成的。
4、随机森林输出的结果是采用投票的结果,而GBDT则是采用将所有树预测结果进行累加。
5、随机森林对数据的异常值不敏感,而GBDT对异常值就非常敏感。
6、随机森林是通过减少模型的方差提供模型性能,而GBDT则是减少偏差。
“模型应该被视为近似值,计量经济学理论应该认真对待这一点”
所有的理论都自然而然地遵循 “如果这是一个过程,那么我们就显示出对真实参数的收敛性 “的思路。收敛性很重要,但这是一个很大的假设。无论是否存在这样的过程,这样的真实模型,我们都不知道它是什么。同样,特别是在社会科学领域,即使有一个真正的GDP,你可以认为它是可变的。
这种讨论引起了模型的组合,或者预测未来的组合。如果我们不知道潜在的真相,结合不同的选择,或不同的建模方法可能会产生更好的结果。
模型平均
让我们使用 3 种不同的模型对时间序列数据进行预测。简单回归 (OLS)、提升树和随机森林。一旦获得了三个预测,我们就可以对它们进行平均。
# 加载代码运行所需的软件包。如果你缺少任何软件包,先安装。
tem <- lappy(c("randomoest", "gb", "quanteg"), librry, charter.oly=T)
# 回归模型。
moelm <- lm(y~x1+x2, data=f)
molrf <- ranmFrst(y~x1+x2, dta=df)
mogm <- gb(ata=df, g.x=1:2, b.y=4
faiy = "gssian", tre.comle = 5, eain.rate = 0.01, bg.fratn = 0.5)
# 现在我们对样本外的预测。
#-------------------------------
Tt_ofsamp <- 500
boosf <- pbot(df\_new$x1, df\_new$x2)
rfft <- pf(df\_new$x1, df\_new$x2)
lmt <- pm(df\_new$x1, df\_new$x2)
# 绑定预测
mtfht <- cbind(bo\_hat, f\_fat, lm_at)
# 命名这些列
c("Boosting", "Random Forest", "OLS")
# 定义一个预测组合方案。
# 为结果留出空间。
resls <- st()
# 最初的30个观测值作为初始窗口
# 重新估计新的观测值到达
it_inw = 30
for(i in 1:leth(A_shes)){
A\_nw$y, mt\_fht,Aeng\_hee= A\_scmes\[i, n_wiow = intwdow )
}
# 该函数输出每个预测平均方案的MSE。
# 让我们检查一下各个方法的MSE是多少。
atr <- apy(ma\_ht, 2, fucon(x) (df\_wy - x)^2 )
apy(ma\_er\[nitnow:Tou\_o_saple, \], 2, fncon(x) 100*( man(x) ) )

在这种情况下,最准确的方法是提升。但是,在其他一些情况下,根据情况,随机森林会比提升更好。如果我们使用约束最小二乘法,我们可以获得几乎最准确的结果,但这不需要事先选择 Boosting 、Random Forest 方法。继续介绍性讨论,我们只是不知道哪种模型会提供最佳结果以及何时会这样做。
加权平均模型融合预测
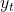 是你的预测变量,
是你的预测变量, 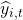 是时间预测
是时间预测 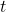 ,从方法
,从方法 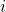 , 和
, 和 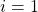 例如OLS,
例如OLS, 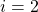 提升树和
提升树和  是随机森林。您可以只取预测的平均值:
是随机森林。您可以只取预测的平均值:
![[\frac{\sum^3_{i=1} \widehat{y}_{i,t} }{3}.] [\frac{\sum^3_{i=1} \widehat{y}_{i,t} }{3}.]](https://img-blog.csdnimg.cn/img_convert/222d08839fe5302a43e42214c759f43d.png)
通常,这个简单的平均值表现非常好。
在 OLS 平均中,我们简单地将预测投影到目标上,所得系数用作权重:
![[\widehat{y}^{combined}_t = \widehat{w}_{0t} + \sum_{i = 1}^3 \widehat{w}_{i,t} \widehat{y}_{它}。] [\widehat{y}^{combined}_t = \widehat{w}_{0t} + \sum_{i = 1}^3 \widehat{w}_{i,t} \widehat{y}_{它}。]](https://img-blog.csdnimg.cn/img_convert/4a1f640802eb47dd963b0adb183b51a8.png)
这是相当不稳定的。所有预测都有相同的目标,因此它们很可能是相关的,这使得估计系数变得困难。稳定系数的一个不错的方法是使用约束优化,即您解决最小二乘问题,但在以下约束下:
![[w_{0t} = 0 \quad \text{and} \quad \sum_{i = 1}^3 w_{it} = 1, \qquad \forall t.] [w_{0t} = 0 \quad \text{and} \quad \sum_{i = 1}^3 w_{it} = 1, \qquad \forall t.]](https://img-blog.csdnimg.cn/img_convert/c7b02ce29511dc91f94d7616fc3947c3.png)
另一种方法是根据预测的准确程度对预测进行平均化,直到基于一些指标如根MSE。我们反转权重,使更准确的(低RMSE)获得更多权重。
![[w_{it} = \frac{\left(\frac{RMSE_{i,t} }{\sum_{i = 1}^3 RMSE_{i,t}}\right)^{-1}}{ \sum_{i = 1}^3 \left(\frac{RMSE_{i,t} }{\sum_{i = 1}^3 RMSE_{i,t}}\right)^{-1} } = \ frac{\frac{1}{RMSE_{i,t}}}{\sum_{i=1}^3\frac{1}{RMSE_{i,t}}}.] [w_{it} = \frac{\left(\frac{RMSE_{i,t} }{\sum_{i = 1}^3 RMSE_{i,t}}\right)^{-1}}{ \sum_{i = 1}^3 \left(\frac{RMSE_{i,t} }{\sum_{i = 1}^3 RMSE_{i,t}}\right)^{-1} } = \ frac{\frac{1}{RMSE_{i,t}}}{\sum_{i=1}^3\frac{1}{RMSE_{i,t}}}.]](https://img-blog.csdnimg.cn/img_convert/2ff12247b2e7ed75339140d54512f9a2.png)
您可以绘制各个方法的权重:
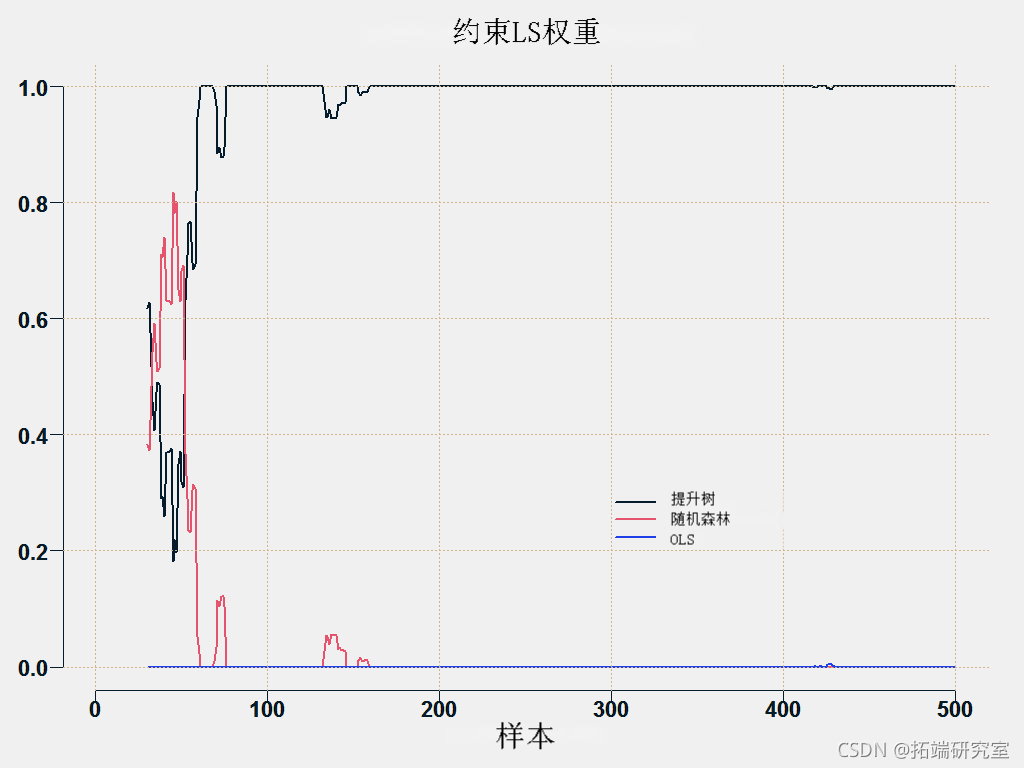
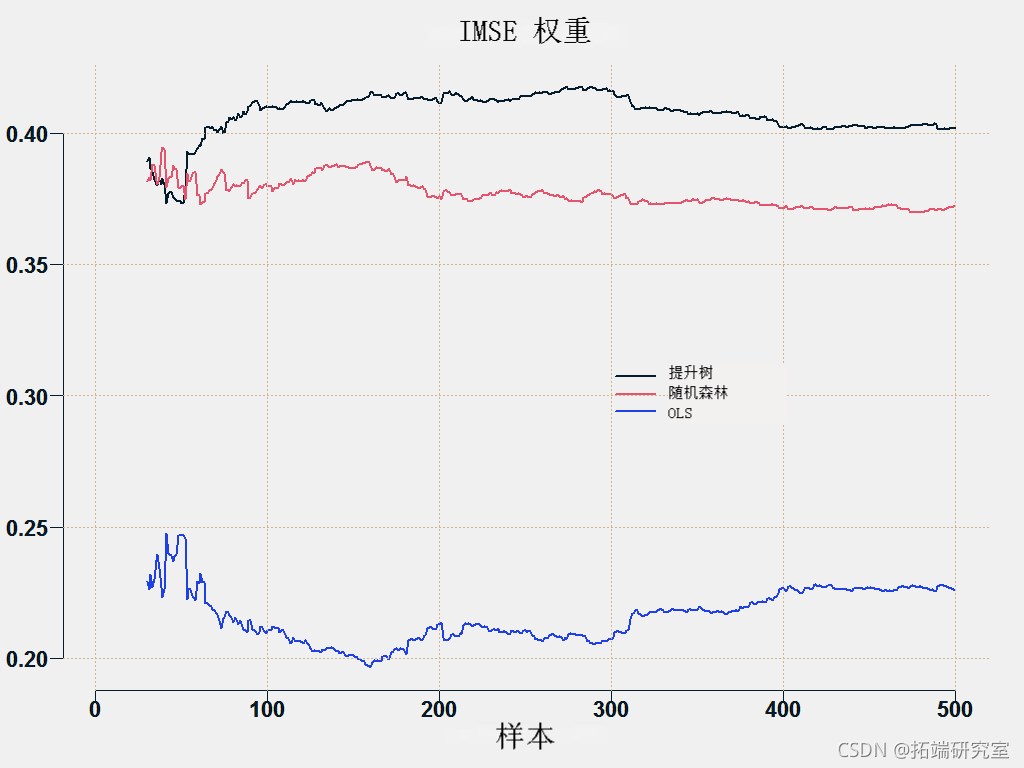
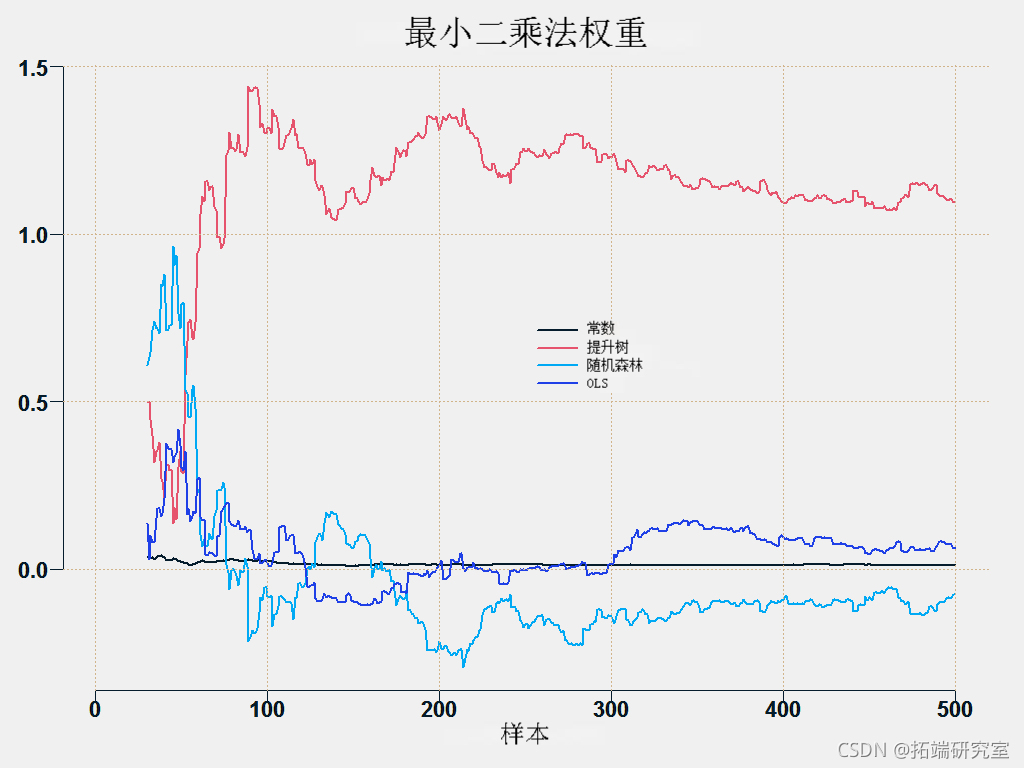
这是预测平均方法。
随时关注您喜欢的主题
## 需要的子程序。
er <- funcion(os, red){ man( (os - ped)^2 ) }
## 不同的预测平均方案
##简单
rd <- aply(a_at, 1, an)
wehs <- trx( 1/p, now = TT, ncl = p)
## OLS权重
wgs <- marx( nol=(p+1)T)
for (i in in_wnow:TT) {
wghs\[i,\] <- lm $oef
pd <- t(eigs\[i,\])%*%c(1, aht\[i,\] )## 稳健的权重
for (i in iitnow:T) {
whs\[i,\] <- q(bs\[1:(i-1)\]~ aft\[1:(i-1),\] )$cef
prd\[i\] <- t(wihs\[i,\] )*c(1, atfha\[i,\])
##基于误差的方差。MSE的倒数
for (i in n_no:TT) {
mp =aply(aerr\[1:(i-1),\]^2,2,ean)/um(aply(mter\[1:(i-1),\]^2,2,man))
wigs\[i,\] <- (1/tmp)/sum(1/tep)
ped\[i\] <- t(wits\[i,\] )%*%c(maat\[i,\] )
##使用约束最小二乘法
for (i in itd:wTT) {
weht\[i,\] <- s1(bs\[1:(i-1)\], a_fat\[1:(i-1),\] )$wigts
red\[i\] <- t(wehs\[i,\])%*%c(aht\[i,\] )
##根据损失的平方函数,挑选出迄今为止表现最好的模型
tmp <- apy(mt\_fat\[-c(1:iit\_wdow),\], 2, ser, obs= obs\[-c(1:ntwiow)\] )
for (i in it_idw:TT) {
wghs\[i,\] <- rp(0,p)
wihts\[i, min(tep)\] <- 1
ped\[i\] <- t(wiht\[i,\] )*c(mht\[i,\] )
} }
MSE <- sr(obs= os\[-c(1:intiow)\], red= red\[-c(1:itwiow)\])
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 Python实现Transformer神经网络时间序列模型可视化分析商超蔬菜销售数据筛选高销量单品预测|附代码数据
Python实现Transformer神经网络时间序列模型可视化分析商超蔬菜销售数据筛选高销量单品预测|附代码数据 Python银行客户数据流失预测SMOTE平衡数据实现神经网络、SVM、决策树、随机森林与超参数调优|附代码数据
Python银行客户数据流失预测SMOTE平衡数据实现神经网络、SVM、决策树、随机森林与超参数调优|附代码数据 Matlab、Python母亲身心健康与婴儿行为特征数据分析WSO-CNN-GRU、GWO-MLP-RF、SEM、SVM、随机森林、Kmeans算法|附代码数据
Matlab、Python母亲身心健康与婴儿行为特征数据分析WSO-CNN-GRU、GWO-MLP-RF、SEM、SVM、随机森林、Kmeans算法|附代码数据 Python主题建模、情感分析酒店评论、工商银行手机APP用户评论:MLP、LSTM、CNN、LDA、SVM、随机森林、朴素贝叶斯
Python主题建模、情感分析酒店评论、工商银行手机APP用户评论:MLP、LSTM、CNN、LDA、SVM、随机森林、朴素贝叶斯



