本文将分析工业指数(DJIA)。工业指数(DIJA)是一个股市指数,表明30家大型上市公司的价值。
最近我们被客户要求撰写关于ARMA-GARCH模型的研究报告。工业指数(DIJA)的价值基于每个组成公司的每股股票价格之和。
可下载资源
本文将尝试回答的主要问题是:
- 这些年来收益率和交易量如何变化?
- 这些年来,收益率和交易量的波动如何变化?
- 我们如何建模收益率波动?
- 我们如何模拟交易量的波动?
什么是ARMA(p,q)模型?
AR(Autoregressive Model)模型即自回归模型,其描述了历史值对当前值的影响。举个实际例子,比如CRSP价值加权指数的月收益率就具有统计上显著的滞后期为1的自相关系数,这个事实说明我们是可以用上一期的CRSP月收益率来预测当期的月收益率的。这也是AR模型的主要作用,用历史值来预测未来,默认历史会重演。其具体表现形式可以表示为:
MA(Moving Average Model)模型即移动平均模型,其认为当前值是自回归模型误差项的累和。关于MA模型的理解,我们既可以将其看成是白噪声序列的简单推广,也可以将其理解为参数受到某种约束的无穷阶AR模型,这个具体推导过程详见教程或相关文献。但MA模型有一个特殊的性质就是其总是弱平稳的,主要在于其表现形式是白噪声序列的有限线性组合,从而其前两阶矩不随时间而变化。MA模型可以表示为:
在介绍完这两种基本的模型后,我们再回到初始介绍的ARMA(p,q)模型上来。 ARMA(Autoregressive moving average model)即自回归移动平均模型。既然AR和MA模型能够刻画绝大部分的时间序列的动态过程,为什么要引入ARMA模型呢?ARMA模型的引入主要是为了解决有些需要高阶的AR或MA模型才能充分描述的动态数据结构,起到了一个类似‘降维’的作用,减少了参数估计量,降低了参数估计难度。结合上面的两个表达式,我们很容易就能够想到ARMA(p,q)的模型表现形式了:
我们这里具体地了解一下其各个参数的含义:如果代表资产的t期对数收益率,则
代表滞后i 期的收益率,而
则表示滞后j 期的扰动项,但扰动项本身是一个均值为0,方差为
的白噪声序列。
和
则分别代表相应变量对应的系数。这些含义也适用于接下来的波动率模型,所以下文不再赘述。
这里澄清一点:对金融中的资产收益率进行建模其实是很少用到ARMA模型的!当然这在前面也提到了,但并不妨碍我们的思路继续进行。
什么是GARCH(1,1)模型?
虽然要多一点真诚,少一些套路,但这里请原谅我要继续按套路出牌了。<邪恶脸>根据前面介绍ARMA的套路,在介绍GARCH之前,我们先来简单了解一下其前身ARCH模型。 ARCH(Autoregressive conditional heteroscedasticity model)即自回归条件异方差模型,其首次出现在Robert-Engle教授于1982年发表在《Econometrica》期刊上的一篇论文中,主要用来解决时间序列的波动性问题。那为什么需要对波动率进行建模呢?概括起来主要有以下几个方面:1.波动率建模提供了一个简单的方法来计算风险管理中一个金融头寸的风险值;2.时间序列的波动率建模能够改进参数估计的有效性和区间预测的精准度;3.市场的波动率本身也可以构建成一个交易工具,用来对冲风险,比如CBOE构建的VIX(波动率指数)就有相应的交易品种在交易所交易。讲到这里,我们来看看ARCH模型的具体表现形式:
根据ARCH模型的表现形式,我们可以知道其一些特点,简单概括一下,因为后面建模会涉及到对性质的利用。ARCH模型分布的尾部相比于正态分布尾部更厚,即其‘扰动’比高斯白噪声序列更容易产生异常值,这与实证研究中资产收益率表现出的异常值多于正态分布一致,而且ARCH模型能够很好地刻画波动率聚集效应。但其也存在着一些缺点,比如说,ARCH模型假定正的扰动和负的扰动对波动率有相同的影响,因为根据其表达式,我们知道波动率依赖于扰动项的平方。但实证研究中,金融资产价格对正的和负的扰动反应是不同的。同时ARCH模型对参数的限制比较强,尤其是对高阶的ARCH模型,参数约束会更加复杂,这导致ARCH模型不能很好地刻画超额峰度,最后ARCH模型给出的波动率预测值会偏高,因为它对收益率序列大的孤立的‘扰动’反应缓慢。
啰嗦了这么多,那到底什么是GARCH模型,其跟我前文介绍的内容又有什么关系嘛?我们知道每一个新的模型的提出都是为了解决之前模型的一些缺点,GARCH也不例外。在ARCH模型中,其假设时间序列的变量的波动幅度(方差)是一个常数,而在实证研究中,学者们早就发现收益率的波动幅度是随时间变化的,并非是固定的值。因此Bollerslev在1986年提出了GARCH(Generalized autoregressive conditional heteroscedasticity model) 模型,即广义自回归条件异方差模型,其在方差的影响因素中增加了方差的滞后项。GARCH模型对ARCH模型的另一大改进是使得高阶ARCH模型退出了历史舞台,因为高阶的ARCH对于波动率建模参数约束太多,并且难以估计,就是上面提到的第二个缺点,这其实又与前面的 ARMA模型相互呼应了。然而GARCH依然没有解决杠杆效应的问题。当然GARCH的衍生模型很好地解决了,不过这是后话了。现在我们先来看一下GARCH(p, q)模型的表现形式:
是不是有一种似曾相识的感觉?是的,没错,GARCH模型可以看作是一个ARMA(p,q)模型的‘变脸’,其将因变量由收益率变为了波动率的平方。至于GARCH的性质大家可以对照上文介绍的ARCH来理解,改进部分我也在前面提到了。这里补充一点,关于波动率模型上面都只是给出了波动率的表达式,其实其还有均值方程以及扰动项方程,完整形式应如下所示:
任何时间序列都由一个均值方程和一个方差方程所组成,普通的ARMA我们忽略了方差方程,因为残差是一个白噪声,没有任何信息可以挖掘了。所以一般只写一个ARMA。而GARCH模型,我们平时都假设均值方程是一个常数,而残差有ARCH效应,所以就focus在残差上,均值略去不写。
所谓的ARMA-GARCH就是分别对均值和方差建模。即均值满足ARMA过程,残差满足GARCH过程的一个随机过程。
总结:
ARMA model: x~ARMA(p,q)+e, where e is a white noise
GARCH model: x~c+e, where c is a constant, e^2 follows a GARCH(p,q) process
ARMA-GARCH model: x~ARMA(p,q)+e, where e^2 follows a GARCH(m,n) process
为此,本文按以下内容划分:
第1部分: 获取每日和每周对数收益的 数据,摘要和图
第2部分:获取每日交易量及其对数比率的数据,摘要和图
第3部分: 每日对数收益率分析和GARCH模型定义
第4部分: 每日交易量分析和GARCH模型定义
获取数据
利用quantmod软件包中提供的getSymbols()函数,我们可以获得2007年至2018年底的工业平均指数。
getSymbols("^DJI", from = "2007-01-01", to = "2019-01-01")
dim(DJI)
## [1] 3020 6
class(DJI)
## [1] "xts" "zoo"让我们看一下DJI xts对象,它提供了六个时间序列,我们可以看到。
head(DJI)
## DJI.Open DJI.High DJI.Low DJI.Close DJI.Volume DJI.Adjusted
## 2007-01-03 12459.54 12580.35 12404.82 12474.52 327200000 12474.52
## 2007-01-04 12473.16 12510.41 12403.86 12480.69 259060000 12480.69
## 2007-01-05 12480.05 12480.13 12365.41 12398.01 235220000 12398.01
## 2007-01-08 12392.01 12445.92 12337.37 12423.49 223500000 12423.49
## 2007-01-09 12424.77 12466.43 12369.17 12416.60 225190000 12416.60
## 2007-01-10 12417.00 12451.61 12355.63 12442.16 226570000 12442.16
tail(DJI)
## DJI.Open DJI.High DJI.Low DJI.Close DJI.Volume DJI.Adjusted
## 2018-12-21 22871.74 23254.59 22396.34 22445.37 900510000 22445.37
## 2018-12-24 22317.28 22339.87 21792.20 21792.20 308420000 21792.20
## 2018-12-26 21857.73 22878.92 21712.53 22878.45 433080000 22878.45
## 2018-12-27 22629.06 23138.89 22267.42 23138.82 407940000 23138.82
## 2018-12-28 23213.61 23381.88 22981.33 23062.40 336510000 23062.40
## 2018-12-31 23153.94 23333.18 23118.30 23327.46 288830000 23327.46更准确地说,我们有可用的OHLC(开盘,高,低,收盘)指数值,调整后的收盘价和交易量。在这里,我们可以看到生成的相应图表。
我们在此分析调整后的收盘价。
DJI[,"DJI.Adjusted"]
简单对数收益率
简单的收益定义为:
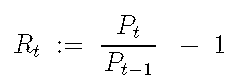
对数收益率定义为:
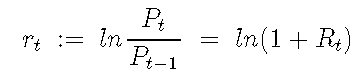
我们计算对数收益率。
CalculateReturns(dj_close, method = "log")
让我们看看。
head(dj_ret)
## DJI.Adjusted
## 2007-01-04 0.0004945580
## 2007-01-05 -0.0066467273
## 2007-01-08 0.0020530973
## 2007-01-09 -0.0005547987
## 2007-01-10 0.0020564627
## 2007-01-11 0.0058356461
tail(dj_ret)
## DJI.Adjusted
## 2018-12-21 -0.018286825
## 2018-12-24 -0.029532247
## 2018-12-26 0.048643314
## 2018-12-27 0.011316355
## 2018-12-28 -0.003308137
## 2018-12-31 0.011427645给出了下面的图。
可以看到波动率的急剧上升和下降。第3部分将对此进行深入验证。
辅助函数
我们需要一些辅助函数来简化一些基本的数据转换,摘要和绘图。
1.从xts转换为带有year and value列的数据框。这样就可以进行年度总结和绘制。
df_t <- data.frame(year = factor(year(index(data_xts))), value = coredata(data_xts))
colnames(df_t) <- c( "year", "value")
2.摘要统计信息,用于存储为数据框列的数据。
rownames(basicStats(rnorm(10,0,1))) # 基本统计数据输出行名称
with(dataset, tapply(value, year, basicStats))3.返回关联的列名。
colnames(basicstats[r, which(basicstats[r,] > threshold), drop = FALSE])4.基于年的面板箱线图。
p <- ggplot(data = data, aes(x = year, y = value)) + theme_bw() + theme(legend.position = "none") + geom_boxplot(fill = "blue")5.密度图,以年份为基准。
p <- ggplot(data = data, aes(x = value)) + geom_density(fill = "lightblue")
p <- p + facet_wrap(. ~ year)
6.基于年份的QQ图。
p <- ggplot(data = dataset, aes(sample = value)) + stat_qq(colour = "blue") + stat_qq_line()
p <- p + facet_wrap(. ~ year)
7. Shapiro检验
pvalue <- function (v) { shapiro.test(v)$p.value}每日对数收益率探索性分析
我们将原始的时间序列转换为具有年和值列的数据框。这样可以按年简化绘图和摘要。
head(ret_df)
## year value
## 1 2007 0.0004945580
## 2 2007 -0.0066467273
## 3 2007 0.0020530973
## 4 2007 -0.0005547987
## 5 2007 0.0020564627
## 6 2007 0.0058356461
tail(ret_df)
## year value
## 3014 2018 -0.018286825
## 3015 2018 -0.029532247
## 3016 2018 0.048643314
## 3017 2018 0.011316355
## 3018 2018 -0.003308137
## 3019 2018 0.011427645基本统计摘要
给出了基本统计摘要。
## 2007 2008 2009 2010 2011
## nobs 250.000000 253.000000 252.000000 252.000000 252.000000
## NAs 0.000000 0.000000 0.000000 0.000000 0.000000
## Minimum -0.033488 -0.082005 -0.047286 -0.036700 -0.057061
## Maximum 0.025223 0.105083 0.066116 0.038247 0.041533
## 1. Quartile -0.003802 -0.012993 -0.006897 -0.003853 -0.006193
## 3. Quartile 0.005230 0.007843 0.008248 0.004457 0.006531
## Mean 0.000246 -0.001633 0.000684 0.000415 0.000214
## Median 0.001098 -0.000890 0.001082 0.000681 0.000941
## Sum 0.061427 -0.413050 0.172434 0.104565 0.053810
## SE Mean 0.000582 0.001497 0.000960 0.000641 0.000837
## LCL Mean -0.000900 -0.004580 -0.001207 -0.000848 -0.001434
## UCL Mean 0.001391 0.001315 0.002575 0.001678 0.001861
## Variance 0.000085 0.000567 0.000232 0.000104 0.000176
## Stdev 0.009197 0.023808 0.015242 0.010182 0.013283
## Skewness -0.613828 0.224042 0.070840 -0.174816 -0.526083
## Kurtosis 1.525069 3.670796 2.074240 2.055407 2.453822
## 2012 2013 2014 2015 2016
## nobs 250.000000 252.000000 252.000000 252.000000 252.000000
## NAs 0.000000 0.000000 0.000000 0.000000 0.000000
## Minimum -0.023910 -0.023695 -0.020988 -0.036402 -0.034473
## Maximum 0.023376 0.023263 0.023982 0.038755 0.024384
## 1. Quartile -0.003896 -0.002812 -0.002621 -0.005283 -0.002845
## 3. Quartile 0.004924 0.004750 0.004230 0.005801 0.004311
## Mean 0.000280 0.000933 0.000288 -0.000090 0.000500
## Median -0.000122 0.001158 0.000728 -0.000211 0.000738
## Sum 0.070054 0.235068 0.072498 -0.022586 0.125884
## SE Mean 0.000470 0.000403 0.000432 0.000613 0.000501
## LCL Mean -0.000645 0.000139 -0.000564 -0.001298 -0.000487
## UCL Mean 0.001206 0.001727 0.001139 0.001118 0.001486
## Variance 0.000055 0.000041 0.000047 0.000095 0.000063
## Stdev 0.007429 0.006399 0.006861 0.009738 0.007951
## Skewness 0.027235 -0.199407 -0.332766 -0.127788 -0.449311
## Kurtosis 0.842890 1.275821 1.073234 1.394268 2.079671
## 2017 2018
## nobs 251.000000 251.000000
## NAs 0.000000 0.000000
## Minimum -0.017930 -0.047143
## Maximum 0.014468 0.048643
## 1. Quartile -0.001404 -0.005017
## 3. Quartile 0.003054 0.005895
## Mean 0.000892 -0.000231
## Median 0.000655 0.000695
## Sum 0.223790 -0.057950
## SE Mean 0.000263 0.000714
## LCL Mean 0.000373 -0.001637
## UCL Mean 0.001410 0.001175
## Variance 0.000017 0.000128
## Stdev 0.004172 0.011313
## Skewness -0.189808 -0.522618
## Kurtosis 2.244076 2.802996在下文中,我们对上述一些相关指标进行了具体评论。
随时关注您喜欢的主题
平均值
每日对数收益率具有正平均值的年份是:
filter_stats(stats, "Mean", 0)
## [1] "2007" "2009" "2010" "2011" "2012" "2013" "2014" "2016" "2017"按升序排列。
## 2008 2018 2015 2011 2007 2012 2014
## Mean -0.001633 -0.000231 -9e-05 0.000214 0.000246 0.00028 0.000288
## 2010 2016 2009 2017 2013
## Mean 0.000415 5e-04 0.000684 0.000892 0.000933中位数
正中位数是:
filter_stats(dj_stats, "Median", 0)
## [1] "2007" "2009" "2010" "2011" "2013" "2014" "2016" "2017" "2018"以升序排列。
## 2008 2015 2012 2017 2010 2018 2014
## Median -0.00089 -0.000211 -0.000122 0.000655 0.000681 0.000695 0.000728
## 2016 2011 2009 2007 2013
## Median 0.000738 0.000941 0.001082 0.001098 0.001158偏度
偏度(Skewness)可以用来度量随机变量概率分布的不对称性。
公式: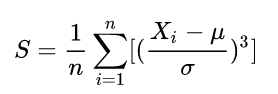
其中 ![]() 是均值,
是均值, ![]() 是标准差。
是标准差。
几何意义:
偏度的取值范围为(-∞,+∞)
当偏度<0时,概率分布图左偏(也叫负偏分布,其偏度<0)。
当偏度=0时,表示数据相对均匀的分布在平均值两侧,不一定是绝对的对称分布。
当偏度>0时,概率分布图右偏(也叫正偏分布,其偏度>0)。
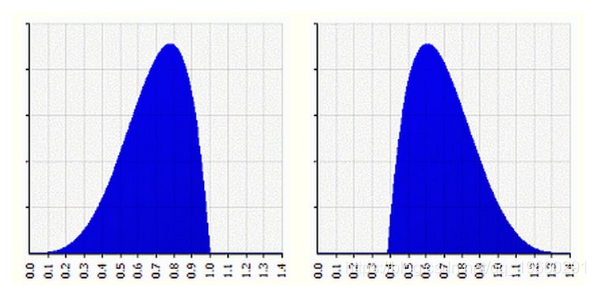
例如上图中,左图形状左偏,右图形状右偏。
每日对数收益出现正偏的年份是:
## [1] "2008" "2009" "2012"按升序返回对数偏度。
stats["Skewness",order(stats["Skewness",
## 2007 2011 2018 2016 2014 2013
## Skewness -0.613828 -0.526083 -0.522618 -0.449311 -0.332766 -0.199407
## 2017 2010 2015 2012 2009 2008
## Skewness -0.189808 -0.174816 -0.127788 0.027235 0.07084 0.224042峰度
峰度(Kurtosis)可以用来度量随机变量概率分布的陡峭程度。
公式:
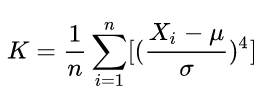
其中 ![]() 是均值,
是均值, ![]() 是标准差。
是标准差。
几何意义:
峰度的取值范围为[1,+∞),完全服从正态分布的数据的峰度值为 3,峰度值越大,概率分布图越高尖,峰度值越小,越矮胖。

例如上图中,左图是标准正太分布,峰度=3,右图的峰度=4,可以看到右图比左图更高尖。
通常我们将峰度值减去3,也被称为超值峰度(Excess Kurtosis),这样正态分布的峰度值等于0,当峰度值>0,则表示该数据分布与正态分布相比较为高尖,当峰度值<0,则表示该数据分布与正态分布相比较为矮胖。
每日对数收益出现超值峰度的年份是:
## [1] "2007" "2008" "2009" "2010" "2011" "2012" "2013" "2014" "2015" "2016"
## [11] "2017" "2018"按升序返回超值峰度。
## 2012 2014 2013 2015 2007 2010 2009
## Kurtosis 0.84289 1.073234 1.275821 1.394268 1.525069 2.055407 2.07424
## 2016 2017 2011 2018 2008
## Kurtosis 2.079671 2.244076 2.453822 2.802996 3.6707962018年的峰度最接近2008年。
箱形图
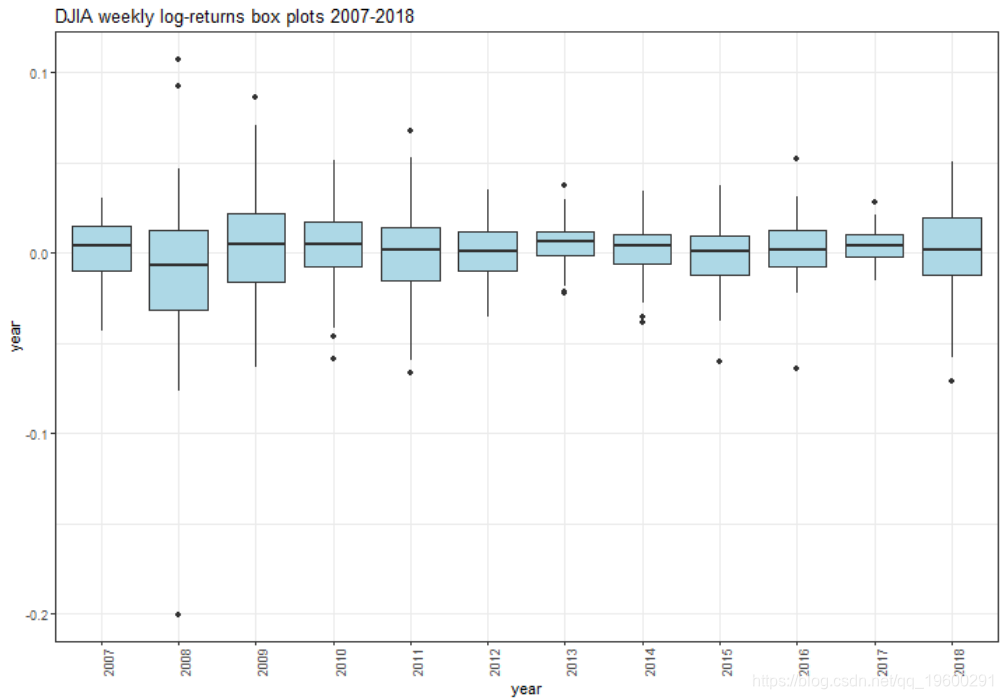
我们可以看到2008年出现了最极端的值。从2009年开始,除了2011年和2015年以外,其他所有值的范围都变窄了。但是,与2017年和2018年相比,产生极端值的趋势明显改善。
密度图
densityplot(ret_df)
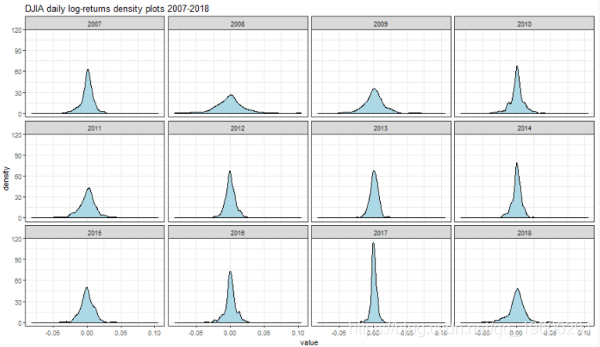
2007年具有显着的负偏。2008年的特点是平坦。2017年的峰值与2018年的平坦度和左偏一致。
shapiro检验
shapirot(ret_df)
## result
## 2007 5.989576e-07
## 2008 5.782666e-09
## 2009 1.827967e-05
## 2010 3.897345e-07
## 2011 5.494349e-07
## 2012 1.790685e-02
## 2013 8.102500e-03
## 2014 1.750036e-04
## 2015 5.531137e-03
## 2016 1.511435e-06
## 2017 3.304529e-05
## 2018 1.216327e-07正态的零假设在2007-2018年的所有年份均被拒绝。
每周对数收益率探索性分析
可以从每日对数收益率开始计算每周对数收益率。让我们假设分析第{t-4,t-3,t-2,t-1,t}天的交易周,并知道第t-5天(前一周的最后一天)的收盘价。我们将每周的对数收益率定义为:
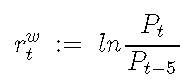
可以写为:
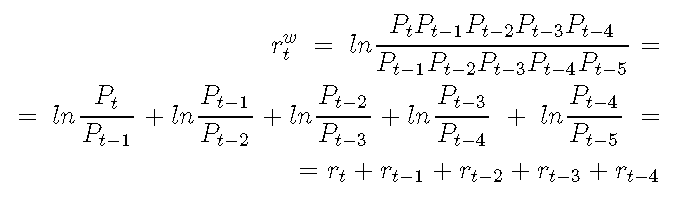
因此,每周对数收益率是应用于交易周窗口的每日对数收益率之和。
我们来看看每周的对数收益率。

该图显示波动率急剧上升和下降。我们将原始时间序列数据转换为数据框。
head(weekly_ret_df)
## year value
## 1 2007 -0.0061521694
## 2 2007 0.0126690596
## 3 2007 0.0007523559
## 4 2007 -0.0062677053
## 5 2007 0.0132434177
## 6 2007 -0.0057588519
tail(weekly_ret_df)
## year value
## 622 2018 0.05028763
## 623 2018 -0.04605546
## 624 2018 -0.01189714
## 625 2018 -0.07114867
## 626 2018 0.02711928
## 627 2018 0.01142764基本统计摘要
dataframe_basicstats(weekly_ret_df)
## 2007 2008 2009 2010 2011 2012
## nobs 52.000000 52.000000 53.000000 52.000000 52.000000 52.000000
## NAs 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000
## Minimum -0.043199 -0.200298 -0.063736 -0.058755 -0.066235 -0.035829
## Maximum 0.030143 0.106977 0.086263 0.051463 0.067788 0.035316
## 1. Quartile -0.009638 -0.031765 -0.015911 -0.007761 -0.015485 -0.010096
## 3. Quartile 0.014808 0.012682 0.022115 0.016971 0.014309 0.011887
## Mean 0.001327 -0.008669 0.003823 0.002011 0.001035 0.001102
## Median 0.004244 -0.006811 0.004633 0.004529 0.001757 0.001166
## Sum 0.069016 -0.450811 0.202605 0.104565 0.053810 0.057303
## SE Mean 0.002613 0.006164 0.004454 0.003031 0.003836 0.002133
## LCL Mean -0.003919 -0.021043 -0.005115 -0.004074 -0.006666 -0.003181
## UCL Mean 0.006573 0.003704 0.012760 0.008096 0.008736 0.005384
## Variance 0.000355 0.001975 0.001051 0.000478 0.000765 0.000237
## Stdev 0.018843 0.044446 0.032424 0.021856 0.027662 0.015382
## Skewness -0.680573 -0.985740 0.121331 -0.601407 -0.076579 -0.027302
## Kurtosis -0.085887 5.446623 -0.033398 0.357708 0.052429 -0.461228
## 2013 2014 2015 2016 2017 2018
## nobs 52.000000 52.000000 53.000000 52.000000 52.000000 53.000000
## NAs 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000
## Minimum -0.022556 -0.038482 -0.059991 -0.063897 -0.015317 -0.071149
## Maximum 0.037702 0.034224 0.037693 0.052243 0.028192 0.050288
## 1. Quartile -0.001738 -0.006378 -0.012141 -0.007746 -0.002251 -0.011897
## 3. Quartile 0.011432 0.010244 0.009620 0.012791 0.009891 0.019857
## Mean 0.004651 0.001756 -0.000669 0.002421 0.004304 -0.001093
## Median 0.006360 0.003961 0.000954 0.001947 0.004080 0.001546
## Sum 0.241874 0.091300 -0.035444 0.125884 0.223790 -0.057950
## SE Mean 0.001828 0.002151 0.002609 0.002436 0.001232 0.003592
## LCL Mean 0.000981 -0.002563 -0.005904 -0.002470 0.001830 -0.008302
## UCL Mean 0.008322 0.006075 0.004567 0.007312 0.006778 0.006115
## Variance 0.000174 0.000241 0.000361 0.000309 0.000079 0.000684
## Stdev 0.013185 0.015514 0.018995 0.017568 0.008886 0.026154
## Skewness -0.035175 -0.534403 -0.494963 -0.467158 0.266281 -0.658951
## Kurtosis -0.200282 0.282354 0.665460 2.908942 -0.124341 -0.000870在下文中,我们对上述一些相关指标进行了具体评论。
平均值
每周对数收益呈正平均值的年份是:
## [1] "2007" "2009" "2010" "2011" "2012" "2013" "2014" "2016" "2017"所有平均值按升序排列。
## 2008 2018 2015 2011 2012 2007 2014
## Mean -0.008669 -0.001093 -0.000669 0.001035 0.001102 0.001327 0.001756
## 2010 2016 2009 2017 2013
## Mean 0.002011 0.002421 0.003823 0.004304 0.004651中位数
中位数是:
## [1] "2007" "2009" "2010" "2011" "2012" "2013" "2014" "2015" "2016" "2017"
## [11] "2018"所有中值按升序排列。
## 2008 2015 2012 2018 2011 2016 2014
## Median -0.006811 0.000954 0.001166 0.001546 0.001757 0.001947 0.003961
## 2017 2007 2010 2009 2013
## Median 0.00408 0.004244 0.004529 0.004633 0.00636偏度
出现正偏的年份是:
stats(stats, "Skewness", 0)
## [1] "2009" "2017"所有偏度按升序排列。
stats["Skewness",order(stats["Skewness",,])]
## 2008 2007 2018 2010 2014 2015
## Skewness -0.98574 -0.680573 -0.658951 -0.601407 -0.534403 -0.494963
## 2016 2011 2013 2012 2009 2017
## Skewness -0.467158 -0.076579 -0.035175 -0.027302 0.121331 0.266281峰度
出现正峰度的年份是:
filter_stats(stats, "Kurtosis", 0) ## [1] "2008" "2010" "2011" "2014" "2015" "2016"峰度值都按升序排列。
## 2012 2013 2017 2007 2009 2018
## Kurtosis -0.461228 -0.200282 -0.124341 -0.085887 -0.033398 -0.00087
## 2011 2014 2010 2015 2016 2008
## Kurtosis 0.052429 0.282354 0.357708 0.66546 2.908942 5.4466232008年也是每周峰度最高的年份。但是,在这种情况下,2017年的峰度为负,而2016年的峰度为第二。
箱形图
密度图

shapiro检验
shapirot(weekly_df)
## result
## 2007 0.0140590311
## 2008 0.0001397267
## 2009 0.8701335006
## 2010 0.0927104389
## 2011 0.8650874270
## 2012 0.9934600084
## 2013 0.4849043121
## 2014 0.1123139646
## 2015 0.3141519756
## 2016 0.0115380989
## 2017 0.9465281164
## 2018 0.0475141869零假设在2007、2008、2016年被拒绝。
QQ图
在2008年尤其明显地违背正态分布的情况。
交易量探索性分析
在这一部分中,本文将分析道琼斯工业平均指数(DJIA)的交易量。
获取数据
每日量探索性分析
我们绘制每日交易量。
vol <- DJI[,"DJI.Volume"]
plot(vol)值得注意的是,2017年初的水平跃升,我们将在第4部分中进行研究。我们将时间序列数据和时间轴索引转换为数据框。
head(dj_vol_df)
## year value
## 1 2007 327200000
## 2 2007 259060000
## 3 2007 235220000
## 4 2007 223500000
## 5 2007 225190000
## 6 2007 226570000
tail(dj_vol_df)
## year value
## 3015 2018 900510000
## 3016 2018 308420000
## 3017 2018 433080000
## 3018 2018 407940000
## 3019 2018 336510000
## 3020 2018 288830000基本统计摘要
## 2007 2008 2009 2010
## nobs 2.510000e+02 2.530000e+02 2.520000e+02 2.520000e+02
## NAs 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
## Minimum 8.640000e+07 6.693000e+07 5.267000e+07 6.840000e+07
## Maximum 4.571500e+08 6.749200e+08 6.729500e+08 4.598900e+08
## 1. Quartile 2.063000e+08 2.132100e+08 1.961850e+08 1.633400e+08
## 3. Quartile 2.727400e+08 3.210100e+08 3.353625e+08 2.219025e+08
## Mean 2.449575e+08 2.767164e+08 2.800537e+08 2.017934e+08
## Median 2.350900e+08 2.569700e+08 2.443200e+08 1.905050e+08
## Sum 6.148432e+10 7.000924e+10 7.057354e+10 5.085193e+10
## SE Mean 3.842261e+06 5.965786e+06 7.289666e+06 3.950031e+06
## LCL Mean 2.373901e+08 2.649672e+08 2.656970e+08 1.940139e+08
## UCL Mean 2.525248e+08 2.884655e+08 2.944104e+08 2.095728e+08
## Variance 3.705505e+15 9.004422e+15 1.339109e+16 3.931891e+15
## Stdev 6.087286e+07 9.489163e+07 1.157199e+08 6.270480e+07
## Skewness 9.422400e-01 1.203283e+00 1.037015e+00 1.452082e+00
## Kurtosis 1.482540e+00 2.064821e+00 6.584810e-01 3.214065e+00
## 2011 2012 2013 2014
## nobs 2.520000e+02 2.500000e+02 2.520000e+02 2.520000e+02
## NAs 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
## Minimum 8.410000e+06 4.771000e+07 3.364000e+07 4.287000e+07
## Maximum 4.799800e+08 4.296100e+08 4.200800e+08 6.554500e+08
## 1. Quartile 1.458775e+08 1.107150e+08 9.488000e+07 7.283000e+07
## 3. Quartile 1.932400e+08 1.421775e+08 1.297575e+08 9.928000e+07
## Mean 1.804133e+08 1.312606e+08 1.184434e+08 9.288516e+07
## Median 1.671250e+08 1.251950e+08 1.109250e+08 8.144500e+07
## Sum 4.546415e+10 3.281515e+10 2.984773e+10 2.340706e+10
## SE Mean 3.897738e+06 2.796503e+06 2.809128e+06 3.282643e+06
## LCL Mean 1.727369e+08 1.257528e+08 1.129109e+08 8.642012e+07
## UCL Mean 1.880897e+08 1.367684e+08 1.239758e+08 9.935019e+07
## Variance 3.828475e+15 1.955108e+15 1.988583e+15 2.715488e+15
## Stdev 6.187468e+07 4.421660e+07 4.459353e+07 5.211034e+07
## Skewness 1.878239e+00 3.454971e+00 3.551752e+00 6.619268e+00
## Kurtosis 5.631080e+00 1.852581e+01 1.900989e+01 5.856136e+01
## 2015 2016 2017 2018
## nobs 2.520000e+02 2.520000e+02 2.510000e+02 2.510000e+02
## NAs 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
## Minimum 4.035000e+07 4.589000e+07 1.186100e+08 1.559400e+08
## Maximum 3.445600e+08 5.734700e+08 6.357400e+08 9.005100e+08
## 1. Quartile 8.775250e+07 8.224250e+07 2.695850e+08 2.819550e+08
## 3. Quartile 1.192150e+08 1.203550e+08 3.389950e+08 4.179200e+08
## Mean 1.093957e+08 1.172089e+08 3.112396e+08 3.593710e+08
## Median 1.021000e+08 9.410500e+07 2.996700e+08 3.414700e+08
## Sum 2.756772e+10 2.953664e+10 7.812114e+10 9.020213e+10
## SE Mean 2.433611e+06 4.331290e+06 4.376432e+06 6.984484e+06
## LCL Mean 1.046028e+08 1.086786e+08 3.026202e+08 3.456151e+08
## UCL Mean 1.141886e+08 1.257392e+08 3.198590e+08 3.731270e+08
## Variance 1.492461e+15 4.727538e+15 4.807442e+15 1.224454e+16
## Stdev 3.863238e+07 6.875709e+07 6.933572e+07 1.106550e+08
## Skewness 3.420032e+00 3.046742e+00 1.478708e+00 1.363823e+00
## Kurtosis 1.612326e+01 1.122161e+01 3.848619e+00 3.277164e+00在下文中,我们对上面显示的一些相关指标进行了评论。
平均值
每日交易量具有正平均值的年份是:
## [1] "2007" "2008" "2009" "2010" "2011" "2012" "2013" "2014" "2015" "2016"
## [11] "2017" "2018"所有每日交易量均值按升序排列。
## 2014 2015 2016 2013 2012 2011 2010
## Mean 92885159 109395714 117208889 118443373 131260600 180413294 201793373
## 2007 2008 2009 2017 2018
## Mean 244957450 276716364 280053730 311239602 359371036中位数
每日交易量中位数为正的年份是:
## [1] "2007" "2008" "2009" "2010" "2011" "2012" "2013" "2014" "2015" "2016"
## [11] "2017" "2018"所有每日成交量中值均按升序排列。
## 2014 2016 2015 2013 2012 2011 2010
## Median 81445000 94105000 102100000 110925000 125195000 167125000 190505000
## 2007 2009 2008 2017 2018
## Median 235090000 244320000 256970000 299670000 341470000偏度
每日交易量出现正偏的年份是:
## [1] "2007" "2008" "2009" "2010" "2011" "2012" "2013" "2014" "2015" "2016"
## [11] "2017" "2018"每日交易量偏度值均按升序排列。
## 2007 2009 2008 2018 2010 2017 2011
## Skewness 0.94224 1.037015 1.203283 1.363823 1.452082 1.478708 1.878239
## 2016 2015 2012 2013 2014
## Skewness 3.046742 3.420032 3.454971 3.551752 6.619268峰度
有正峰度的年份是:
## [1] "2007" "2008" "2009" "2010" "2011" "2012" "2013" "2014" "2015" "2016"
## [11] "2017" "2018"按升序排列。
## 2009 2007 2008 2010 2018 2017 2011
## Kurtosis 0.658481 1.48254 2.064821 3.214065 3.277164 3.848619 5.63108
## 2016 2015 2012 2013 2014
## Kurtosis 11.22161 16.12326 18.52581 19.00989 58.56136箱形图
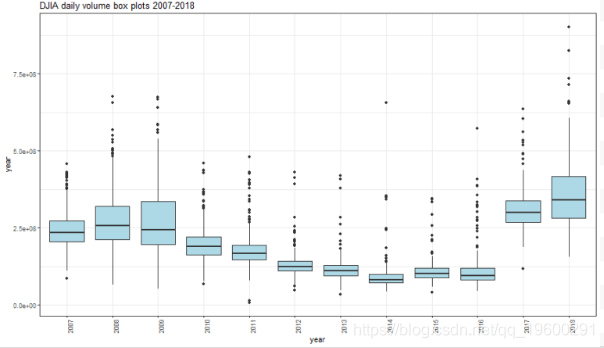
从2010年开始交易量开始下降,2017年出现了显着增长。2018年的交易量甚至超过了2017年和其他年份。
密度图
shapiro检验
## result
## 2007 6.608332e-09
## 2008 3.555102e-10
## 2009 1.023147e-10
## 2010 9.890576e-13
## 2011 2.681476e-16
## 2012 1.866544e-20
## 2013 6.906596e-21
## 2014 5.304227e-27
## 2015 2.739912e-21
## 2016 6.640215e-23
## 2017 4.543843e-12
## 2018 9.288371e-11正态分布的零假设被拒绝。
QQ图
QQplots直观地确认了每日交易量分布的非正态情况。
每日交易量对数比率探索性分析
与对数收益类似,我们可以将交易量对数比率定义为
vt:= ln(Vt/Vt−1)
我们可以通过PerformanceAnalytics包中的CalculateReturns对其进行计算并将其绘制出来。
plot(vol_log_ratio)
将交易量对数比率时间序列数据和时间轴索引映射到数据框。
head(dvol_df)
## year value
## 1 2007 -0.233511910
## 2 2007 -0.096538449
## 3 2007 -0.051109832
## 4 2007 0.007533076
## 5 2007 0.006109458
## 6 2007 0.144221282
tail(vol_df)
## year value
## 3014 2018 0.44563907
## 3015 2018 -1.07149878
## 3016 2018 0.33945998
## 3017 2018 -0.05980236
## 3018 2018 -0.19249224
## 3019 2018 -0.15278959基本统计摘要
## 2007 2008 2009 2010 2011
## nobs 250.000000 253.000000 252.000000 252.000000 252.000000
## NAs 0.000000 0.000000 0.000000 0.000000 0.000000
## Minimum -1.606192 -1.122526 -1.071225 -1.050181 -2.301514
## Maximum 0.775961 0.724762 0.881352 1.041216 2.441882
## 1. Quartile -0.123124 -0.128815 -0.162191 -0.170486 -0.157758
## 3. Quartile 0.130056 0.145512 0.169233 0.179903 0.137108
## Mean -0.002685 0.001203 -0.001973 -0.001550 0.000140
## Median -0.010972 0.002222 -0.031748 -0.004217 -0.012839
## Sum -0.671142 0.304462 -0.497073 -0.390677 0.035162
## SE Mean 0.016984 0.016196 0.017618 0.019318 0.026038
## LCL Mean -0.036135 -0.030693 -0.036670 -0.039596 -0.051141
## UCL Mean 0.030766 0.033100 0.032725 0.036495 0.051420
## Variance 0.072112 0.066364 0.078219 0.094041 0.170850
## Stdev 0.268536 0.257612 0.279677 0.306661 0.413341
## Skewness -0.802037 -0.632586 0.066535 -0.150523 0.407226
## Kurtosis 5.345212 2.616615 1.500979 1.353797 14.554642
## 2012 2013 2014 2015 2016
## nobs 250.000000 252.000000 252.000000 252.000000 252.000000
## NAs 0.000000 0.000000 0.000000 0.000000 0.000000
## Minimum -2.158960 -1.386215 -2.110572 -1.326016 -1.336471
## Maximum 1.292956 1.245202 2.008667 1.130289 1.319713
## 1. Quartile -0.152899 -0.145444 -0.144280 -0.143969 -0.134011
## 3. Quartile 0.144257 0.149787 0.134198 0.150003 0.141287
## Mean 0.001642 -0.002442 0.000200 0.000488 0.004228
## Median -0.000010 -0.004922 0.013460 0.004112 -0.002044
## Sum 0.410521 -0.615419 0.050506 0.123080 1.065480
## SE Mean 0.021293 0.019799 0.023514 0.019010 0.019089
## LCL Mean -0.040295 -0.041435 -0.046110 -0.036952 -0.033367
## UCL Mean 0.043579 0.036551 0.046510 0.037929 0.041823
## Variance 0.113345 0.098784 0.139334 0.091071 0.091826
## Stdev 0.336667 0.314299 0.373274 0.301780 0.303028
## Skewness -0.878227 -0.297951 -0.209417 -0.285918 0.083826
## Kurtosis 8.115847 4.681120 9.850061 4.754926 4.647785
## 2017 2018
## nobs 251.000000 251.000000
## NAs 0.000000 0.000000
## Minimum -0.817978 -1.071499
## Maximum 0.915599 0.926101
## 1. Quartile -0.112190 -0.119086
## 3. Quartile 0.110989 0.112424
## Mean -0.000017 0.000257
## Median -0.006322 0.003987
## Sum -0.004238 0.064605
## SE Mean 0.013446 0.014180
## LCL Mean -0.026500 -0.027671
## UCL Mean 0.026466 0.028185
## Variance 0.045383 0.050471
## Stdev 0.213032 0.224658
## Skewness 0.088511 -0.281007
## Kurtosis 3.411036 4.335748在下文中,我们对一些相关的上述指标进行了具体评论。
平均值
每日交易量对数比率具有正平均值的年份是:
## [1] "2008" "2011" "2012" "2014" "2015" "2016" "2018"所有每日成交量比率的平均值均按升序排列。
## 2007 2013 2009 2010 2017 2011 2014
## Mean -0.002685 -0.002442 -0.001973 -0.00155 -1.7e-05 0.00014 2e-04
## 2018 2015 2008 2012 2016
## Mean 0.000257 0.000488 0.001203 0.001642 0.004228中位数
每日交易量对数比率具有正中位数的年份是:
## [1] "2008" "2014" "2015" "2018"道琼斯所有每日成交量比率的中位数均按升序排列。
## 2009 2011 2007 2017 2013 2010
## Median -0.031748 -0.012839 -0.010972 -0.006322 -0.004922 -0.004217
## 2016 2012 2008 2018 2015 2014
## Median -0.002044 -1e-05 0.002222 0.003987 0.004112 0.01346偏度
每日成交量比率具有正偏的年份是:
## [1] "2009" "2011" "2016" "2017"所有每日成交量比率的平均值均按升序排列。
## 2012 2007 2008 2013 2015 2018
## Skewness -0.878227 -0.802037 -0.632586 -0.297951 -0.285918 -0.281007
## 2014 2010 2009 2016 2017 2011
## Skewness -0.209417 -0.150523 0.066535 0.083826 0.088511 0.407226峰度
有正峰度的年份是:
## [1] "2007" "2008" "2009" "2010" "2011" "2012" "2013" "2014" "2015" "2016"
## [11] "2017" "2018"均按升序排列。
## 2010 2009 2008 2017 2018 2016 2013
## Kurtosis 1.353797 1.500979 2.616615 3.411036 4.335748 4.647785 4.68112
## 2015 2007 2012 2014 2011
## Kurtosis 4.754926 5.345212 8.115847 9.850061 14.55464箱形图
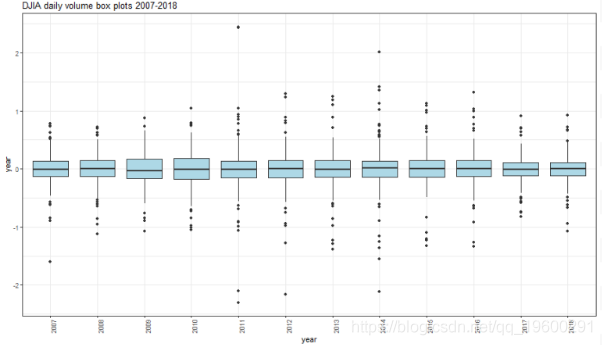
可以在2011、2014和2016年发现正的极端值。在2007、2011、2012、2014年可以发现负的极端值。
密度图
shapiro检验
## result
## 2007 3.695053e-09
## 2008 6.160136e-07
## 2009 2.083475e-04
## 2010 1.500060e-03
## 2011 3.434415e-18
## 2012 8.417627e-12
## 2013 1.165184e-10
## 2014 1.954662e-16
## 2015 5.261037e-11
## 2016 7.144940e-11
## 2017 1.551041e-08
## 2018 3.069196e-09基于报告的p值,我们可以拒绝所有正态分布的零假设。
QQ图
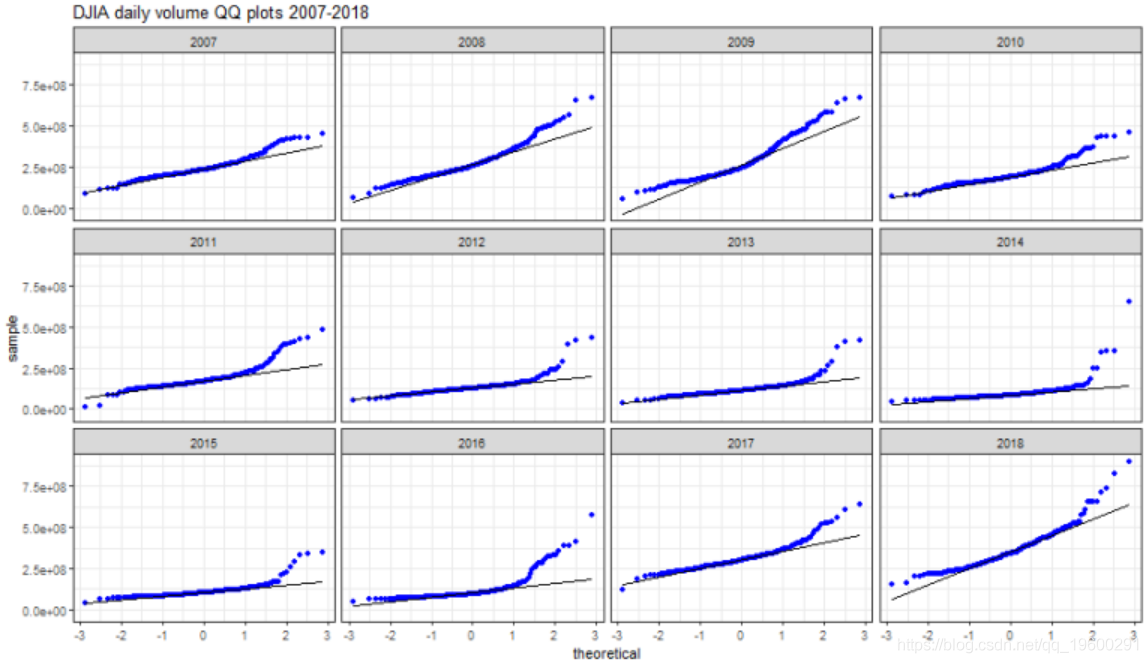
在所有报告的年份都可以发现偏离正态状态。
对数收益率GARCH模型
我将为工业平均指数(DJIA)的每日对数收益率建立一个ARMA-GARCH模型。
这是工业平均指数每日对数收益的图。
plot(ret)
离群值检测
Performance Analytics程序包中的Return.clean函数能够清除异常值。在下面,我们将原始时间序列与调整离群值后的进行比较。
clean(ret, "boudt")
作为对波动率评估的更为保守的方法,本文将以原始时间序列进行分析。
相关图
以下是自相关和偏相关图。
acf(ret)
pacf(dj_ret)
上面的相关图表明p和q> 0的一些ARMA(p,q)模型。将在本分析的该范围内对此进行验证。
单位根检验
我们运行Augmented Dickey-Fuller检验。
##
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression none
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 - 1 + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.081477 -0.004141 0.000762 0.005426 0.098777
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## z.lag.1 -1.16233 0.02699 -43.058 < 2e-16 ***
## z.diff.lag 0.06325 0.01826 3.464 0.000539 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.01157 on 2988 degrees of freedom
## Multiple R-squared: 0.5484, Adjusted R-squared: 0.5481
## F-statistic: 1814 on 2 and 2988 DF, p-value: < 2.2e-16
##
##
## Value of test-statistic is: -43.0578
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau1 -2.58 -1.95 -1.62基于报告的检验统计数据与临界值的比较,我们拒绝单位根存在的零假设。
ARMA模型
现在,我们确定时间序列的ARMA结构,以便对结果残差进行ARCH效应检验。ACF和PACF系数拖尾表明存在ARMA(2,2)。我们利用auto.arima()函数开始构建。
## Series: ret
## ARIMA(2,0,4) with zero mean
##
## Coefficients:
## ar1 ar2 ma1 ma2 ma3 ma4
## 0.4250 -0.8784 -0.5202 0.8705 -0.0335 -0.0769
## s.e. 0.0376 0.0628 0.0412 0.0672 0.0246 0.0203
##
## sigma^2 estimated as 0.0001322: log likelihood=9201.19
## AIC=-18388.38 AICc=-18388.34 BIC=-18346.29
##
## Training set error measures:
## ME RMSE MAE MPE MAPE MASE
## Training set 0.0002416895 0.01148496 0.007505056 NaN Inf 0.6687536
## ACF1
## Training set -0.002537238建议使用ARMA(2,4)模型。但是,ma3系数在统计上并不显着,进一步通过以下方法验证:
## z test of coefficients:
##
## Estimate Std. Error z value Pr(>|z|)
## ar1 0.425015 0.037610 11.3007 < 2.2e-16 ***
## ar2 -0.878356 0.062839 -13.9779 < 2.2e-16 ***
## ma1 -0.520173 0.041217 -12.6204 < 2.2e-16 ***
## ma2 0.870457 0.067211 12.9511 < 2.2e-16 ***
## ma3 -0.033527 0.024641 -1.3606 0.1736335
## ma4 -0.076882 0.020273 -3.7923 0.0001492 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1因此,我们将MA阶q <= 2作为约束。
## Series: dj_ret
## ARIMA(2,0,2) with zero mean
##
## Coefficients:
## ar1 ar2 ma1 ma2
## -0.5143 -0.4364 0.4212 0.3441
## s.e. 0.1461 0.1439 0.1512 0.1532
##
## sigma^2 estimated as 0.0001325: log likelihood=9196.33
## AIC=-18382.66 AICc=-18382.64 BIC=-18352.6
##
## Training set error measures:
## ME RMSE MAE MPE MAPE MASE
## Training set 0.0002287171 0.01150361 0.007501925 Inf Inf 0.6684746
## ACF1
## Training set -0.002414944现在,所有系数都具有统计意义。
## z test of coefficients:
##
## Estimate Std. Error z value Pr(>|z|)
## ar1 -0.51428 0.14613 -3.5192 0.0004328 ***
## ar2 -0.43640 0.14392 -3.0322 0.0024276 **
## ma1 0.42116 0.15121 2.7853 0.0053485 **
## ma2 0.34414 0.15323 2.2458 0.0247139 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1使用ARMA(2,1)和ARMA(1,2)进行的进一步验证得出的AIC值高于ARMA(2,2)。因此,ARMA(2,2)是更可取的。这是结果。
## Series: dj_ret
## ARIMA(2,0,1) with zero mean
##
## Coefficients:
## ar1 ar2 ma1
## -0.4619 -0.1020 0.3646
## s.e. 0.1439 0.0204 0.1438
##
## sigma^2 estimated as 0.0001327: log likelihood=9194.1
## AIC=-18380.2 AICc=-18380.19 BIC=-18356.15
##
## Training set error measures:
## ME RMSE MAE MPE MAPE MASE
## Training set 0.0002370597 0.01151213 0.007522059 Inf Inf 0.6702687
## ACF1
## Training set 0.0009366271
coeftest(auto_model3)
##
## z test of coefficients:
##
## Estimate Std. Error z value Pr(>|z|)
## ar1 -0.461916 0.143880 -3.2104 0.001325 **
## ar2 -0.102012 0.020377 -5.0062 5.552e-07 ***
## ma1 0.364628 0.143818 2.5353 0.011234 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1所有系数均具有统计学意义。
## ARIMA(1,0,2) with zero mean
##
## Coefficients:
## ar1 ma1 ma2
## -0.4207 0.3259 -0.0954
## s.e. 0.1488 0.1481 0.0198
##
## sigma^2 estimated as 0.0001328: log likelihood=9193.01
## AIC=-18378.02 AICc=-18378 BIC=-18353.96
##
## Training set error measures:
## ME RMSE MAE MPE MAPE MASE
## Training set 0.0002387398 0.0115163 0.007522913 Inf Inf 0.6703448
## ACF1
## Training set -0.001958194
coeftest(auto_model4)
##
## z test of coefficients:
##
## Estimate Std. Error z value Pr(>|z|)
## ar1 -0.420678 0.148818 -2.8268 0.004702 **
## ma1 0.325918 0.148115 2.2004 0.027776 *
## ma2 -0.095407 0.019848 -4.8070 1.532e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1所有系数均具有统计学意义。此外,我们使用TSA软件包报告中的eacf()函数。
## AR/MA
## 0 1 2 3 4 5 6 7 8 9 10 11 12 13
## 0 x x x o x o o o o o o o o x
## 1 x x o o x o o o o o o o o o
## 2 x o o x x o o o o o o o o o
## 3 x o x o x o o o o o o o o o
## 4 x x x x x o o o o o o o o o
## 5 x x x x x o o x o o o o o o
## 6 x x x x x x o o o o o o o o
## 7 x x x x x o o o o o o o o o以“ O”为顶点的左上三角形位于(p,q)= {(1,2 ,,(2,2),(1,3)}}内,它表示一组潜在候选对象(p,q)值。ARMA(1,2)模型已经过验证。ARMA(2,2)已经是候选模型。让我们验证ARMA(1,3)。
## Call:
##
## Coefficients:
## ar1 ma1 ma2 ma3
## -0.2057 0.1106 -0.0681 0.0338
## s.e. 0.2012 0.2005 0.0263 0.0215
##
## sigma^2 estimated as 0.0001325: log likelihood = 9193.97, aic = -18379.94
coeftest(arima_model5)
##
## z test of coefficients:
##
## Estimate Std. Error z value Pr(>|z|)
## ar1 -0.205742 0.201180 -1.0227 0.306461
## ma1 0.110599 0.200475 0.5517 0.581167
## ma2 -0.068124 0.026321 -2.5882 0.009647 **
## ma3 0.033832 0.021495 1.5739 0.115501
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1只有一个系数具有统计意义。
结论是,我们选择ARMA(2,2)作为均值模型。现在,我们可以继续进行ARCH效果检验。
ARCH LM检验的原假设是:ARCH模型里所有回归系数是否同时为零。
若概率大,大于给定的显著性水平(比如5%),则序列不存在ARCH效应的,即不能拒绝没有ARCH效应假设, ARCH LM一般是对残差进行检验,在未知残差是否具有ARCH效应时,用OLS后,一般是希望残差检验的相伴概率从1阶就有ARCH效应,即概率从1阶就很小,拒绝假设,但是有些时候是低阶概率大,不能拒绝假设,而到了高阶(一般为7、8阶时)概率小,拒绝假设时,说明高阶是有很强的ARCH效应的,这是正常的表现。
在对序列使用GARCH模型后的残差ARCH LM检验时,就必须期望残差从1阶就表现较大的概率为好,即不能拒绝原假设,残差不再有ARCH效应,说明残差里的信息已经提取干净。
ARCH效应检验
现在,我们可以检验模型残差上是否存在ARCH效应。如果ARCH效应对于我们的时间序列的残差在统计上显着,则需要GARCH模型。
## ARCH LM-test; Null hypothesis: no ARCH effects
##
## data: model_residuals - mean(model_residuals)
## Chi-squared = 986.82, df = 12, p-value < 2.2e-16基于报告的p值,我们拒绝没有ARCH效应的原假设。
粗略地说,平稳。
让我们看一下残差相关图。
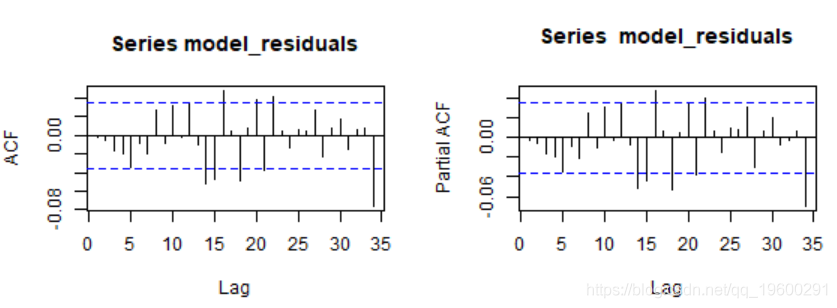
条件波动率
条件均值和方差定义为:
μt:= E(rt | Ft-1)σt2:= Var(rt | Ft-1)= E [(rt-μt)2 | Ft-1]
条件波动率可以计算为条件方差的平方根。
eGARCH模型
将sGARCH作为方差模型的尝试未获得具有统计显着性系数的结果。
而指数GARCH(eGARCH)方差模型能够捕获波动率内的不对称性。要检查DJIA对数收益率内的不对称性,显示汇总统计数据和密度图。
## DAdjusted
## nobs 3019.000000
## NAs 0.000000
## Minimum -0.082005
## Maximum 0.105083
## 1. Quartile -0.003991
## 3. Quartile 0.005232
## Mean 0.000207
## Median 0.000551
## Sum 0.625943
## SE Mean 0.000211
## LCL Mean -0.000206
## UCL Mean 0.000621
## Variance 0.000134
## Stdev 0.011593
## Skewness -0.141370
## Kurtosis 10.200492负偏度值确认分布内不对称性的存在。
这给出了密度图。
我们继续提出eGARCH模型作为方差模型(针对条件方差)。更准确地说,我们将使用ARMA(2,2)作为均值模型,指数GARCH(1,1)作为方差模型对ARMA-GARCH进行建模。
在此之前,我们进一步强调ARMA(0,0)在这种情况下不令人满意。ARMA-GARCH:ARMA(0,0)+ eGARCH(1,1)
##
## *---------------------------------*
## * GARCH Model Fit *
## *---------------------------------*
##
## Conditional Variance Dynamics
## -----------------------------------
## GARCH Model : eGARCH(1,1)
## Mean Model : ARFIMA(0,0,0)
## Distribution : sstd
##
## Optimal Parameters
## ------------------------------------
## Estimate Std. Error t value Pr(>|t|)
## mu 0.000303 0.000117 2.5933 0.009506
## omega -0.291302 0.016580 -17.5699 0.000000
## alpha1 -0.174456 0.013913 -12.5387 0.000000
## beta1 0.969255 0.001770 547.6539 0.000000
## gamma1 0.188918 0.021771 8.6773 0.000000
## skew 0.870191 0.021763 39.9848 0.000000
## shape 6.118380 0.750114 8.1566 0.000000
##
## Robust Standard Errors:
## Estimate Std. Error t value Pr(>|t|)
## mu 0.000303 0.000130 2.3253 0.020055
## omega -0.291302 0.014819 -19.6569 0.000000
## alpha1 -0.174456 0.016852 -10.3524 0.000000
## beta1 0.969255 0.001629 595.0143 0.000000
## gamma1 0.188918 0.031453 6.0063 0.000000
## skew 0.870191 0.022733 38.2783 0.000000
## shape 6.118380 0.834724 7.3298 0.000000
##
## LogLikelihood : 10138.63
##
## Information Criteria
## ------------------------------------
##
## Akaike -6.7119
## Bayes -6.6980
## Shibata -6.7119
## Hannan-Quinn -6.7069
##
## Weighted Ljung-Box Test on Standardized Residuals
## ------------------------------------
## statistic p-value
## Lag[1] 5.475 0.01929
## Lag[2*(p+q)+(p+q)-1][2] 6.011 0.02185
## Lag[4*(p+q)+(p+q)-1][5] 7.712 0.03472
## d.o.f=0
## H0 : No serial correlation
##
## Weighted Ljung-Box Test on Standardized Squared Residuals
## ------------------------------------
## statistic p-value
## Lag[1] 1.342 0.2467
## Lag[2*(p+q)+(p+q)-1][5] 2.325 0.5438
## Lag[4*(p+q)+(p+q)-1][9] 2.971 0.7638
## d.o.f=2
##
## Weighted ARCH LM Tests
## ------------------------------------
## Statistic Shape Scale P-Value
## ARCH Lag[3] 0.3229 0.500 2.000 0.5699
## ARCH Lag[5] 1.4809 1.440 1.667 0.5973
## ARCH Lag[7] 1.6994 2.315 1.543 0.7806
##
## Nyblom stability test
## ------------------------------------
## Joint Statistic: 4.0468
## Individual Statistics:
## mu 0.2156
## omega 1.0830
## alpha1 0.5748
## beta1 0.8663
## gamma1 0.3994
## skew 0.1044
## shape 0.4940
##
## Asymptotic Critical Values (10% 5% 1%)
## Joint Statistic: 1.69 1.9 2.35
## Individual Statistic: 0.35 0.47 0.75
##
## Sign Bias Test
## ------------------------------------
## t-value prob sig
## Sign Bias 1.183 0.23680
## Negative Sign Bias 2.180 0.02932 **
## Positive Sign Bias 1.554 0.12022
## Joint Effect 8.498 0.03677 **
##
##
## Adjusted Pearson Goodness-of-Fit Test:
## ------------------------------------
## group statistic p-value(g-1)
## 1 20 37.24 0.00741
## 2 30 42.92 0.04633
## 3 40 52.86 0.06831
## 4 50 65.55 0.05714
##
##
## Elapsed time : 0.6527421所有系数均具有统计学意义。但是,根据以上报告的p值的标准化残差加权Ljung-Box检验,我们确认该模型无法捕获所有ARCH效果(我们拒绝了残差内无相关性的零假设) )。
作为结论,我们通过在下面所示的GARCH拟合中指定ARMA(2,2)作为均值模型来继续进行。
ARMA-GARCH:ARMA(2,2)+ eGARCH(1,1)
##
## *---------------------------------*
## * GARCH Model Fit *
## *---------------------------------*
##
## Conditional Variance Dynamics
## -----------------------------------
## GARCH Model : eGARCH(1,1)
## Mean Model : ARFIMA(2,0,2)
## Distribution : sstd
##
## Optimal Parameters
## ------------------------------------
## Estimate Std. Error t value Pr(>|t|)
## ar1 -0.47642 0.026115 -18.2433 0
## ar2 -0.57465 0.052469 -10.9523 0
## ma1 0.42945 0.025846 16.6157 0
## ma2 0.56258 0.054060 10.4066 0
## omega -0.31340 0.003497 -89.6286 0
## alpha1 -0.17372 0.011642 -14.9222 0
## beta1 0.96598 0.000027 35240.1590 0
## gamma1 0.18937 0.011893 15.9222 0
## skew 0.84959 0.020063 42.3469 0
## shape 5.99161 0.701313 8.5434 0
##
## Robust Standard Errors:
## Estimate Std. Error t value Pr(>|t|)
## ar1 -0.47642 0.007708 -61.8064 0
## ar2 -0.57465 0.018561 -30.9608 0
## ma1 0.42945 0.007927 54.1760 0
## ma2 0.56258 0.017799 31.6074 0
## omega -0.31340 0.003263 -96.0543 0
## alpha1 -0.17372 0.012630 -13.7547 0
## beta1 0.96598 0.000036 26838.0412 0
## gamma1 0.18937 0.013003 14.5631 0
## skew 0.84959 0.020089 42.2911 0
## shape 5.99161 0.707324 8.4708 0
##
## LogLikelihood : 10140.27
##
## Information Criteria
## ------------------------------------
##
## Akaike -6.7110
## Bayes -6.6911
## Shibata -6.7110
## Hannan-Quinn -6.7039
##
## Weighted Ljung-Box Test on Standardized Residuals
## ------------------------------------
## statistic p-value
## Lag[1] 0.03028 0.8619
## Lag[2*(p+q)+(p+q)-1][11] 5.69916 0.6822
## Lag[4*(p+q)+(p+q)-1][19] 12.14955 0.1782
## d.o.f=4
## H0 : No serial correlation
##
## Weighted Ljung-Box Test on Standardized Squared Residuals
## ------------------------------------
## statistic p-value
## Lag[1] 1.666 0.1967
## Lag[2*(p+q)+(p+q)-1][5] 2.815 0.4418
## Lag[4*(p+q)+(p+q)-1][9] 3.457 0.6818
## d.o.f=2
##
## Weighted ARCH LM Tests
## ------------------------------------
## Statistic Shape Scale P-Value
## ARCH Lag[3] 0.1796 0.500 2.000 0.6717
## ARCH Lag[5] 1.5392 1.440 1.667 0.5821
## ARCH Lag[7] 1.6381 2.315 1.543 0.7933
##
## Nyblom stability test
## ------------------------------------
## Joint Statistic: 4.4743
## Individual Statistics:
## ar1 0.07045
## ar2 0.37070
## ma1 0.07702
## ma2 0.39283
## omega 1.00123
## alpha1 0.49520
## beta1 0.79702
## gamma1 0.51601
## skew 0.07163
## shape 0.55625
##
## Asymptotic Critical Values (10% 5% 1%)
## Joint Statistic: 2.29 2.54 3.05
## Individual Statistic: 0.35 0.47 0.75
##
## Sign Bias Test
## ------------------------------------
## t-value prob sig
## Sign Bias 0.4723 0.63677
## Negative Sign Bias 1.7969 0.07246 *
## Positive Sign Bias 2.0114 0.04438 **
## Joint Effect 7.7269 0.05201 *
##
##
## Adjusted Pearson Goodness-of-Fit Test:
## ------------------------------------
## group statistic p-value(g-1)
## 1 20 46.18 0.0004673
## 2 30 47.73 0.0156837
## 3 40 67.07 0.0034331
## 4 50 65.51 0.0574582
##
##
## Elapsed time : 0.93679所有系数均具有统计学意义。在标准化残差或标准化平方残差内未发现相关性。模型正确捕获所有ARCH效果。然而:
*对于某些模型参数,Nyblom稳定性检验无效假设认为模型参数随时间是恒定的
*正偏差为零的假设在5%的显着性水平上被拒绝;这种检验着重于正面冲击的影响
*拒绝了标准化残差的经验和理论分布相同的Pearson拟合优度检验原假设
注意:ARMA(1,2)+ eGARCH(1,1)拟合还提供统计上显着的系数,标准化残差内没有相关性,标准化平方残差内没有相关性,并且正确捕获了所有ARCH效应。但是,偏差检验在5%时不如ARMA(2,2)+ eGARCH(1,1)模型令人满意。
进一步显示诊断图。
我们用平均模型拟合(红线)和条件波动率(蓝线)显示了原始的对数收益时间序列。
p <- addSeries(mean_model_fit, col = 'red', on = 1)
p <- addSeries(cond_volatility, col = 'blue', on = 1)
p模型方程式
结合ARMA(2,2)和eGARCH模型,我们可以:
yt − ϕ1yt−1 − ϕ2yt−2 = ϕ0 + ut + θ1ut−1 +θ2ut-2ut= σtϵt,ϵt = N(0,1)ln(σt2)=ω+ ∑j = 1q(αjϵt−j2 +γ (ϵt−j–E | ϵt−j |))+ ∑i =1pβiln(σt−12)
使用模型结果系数,结果如下。
yt +0.476 yt-1 +0.575 yt-2 = ut +0.429 ut-1 +0.563 ut-2ut = σtϵt,ϵt = N(0,1)ln(σt2)= -0.313 -0.174ϵt-12 +0.189( ϵt−1–E | ϵt−1 |))+ 0.966 ln(σt−12)
波动率分析
这是由ARMA(2,2)+ eGARCH(1,1)模型得出的条件波动图。
plot(cond_volatility)
显示了年条件波动率的线线图。
pl <- lapply(2007:2018, function(x) { plot(cond_volatility[as.character(x)])
pl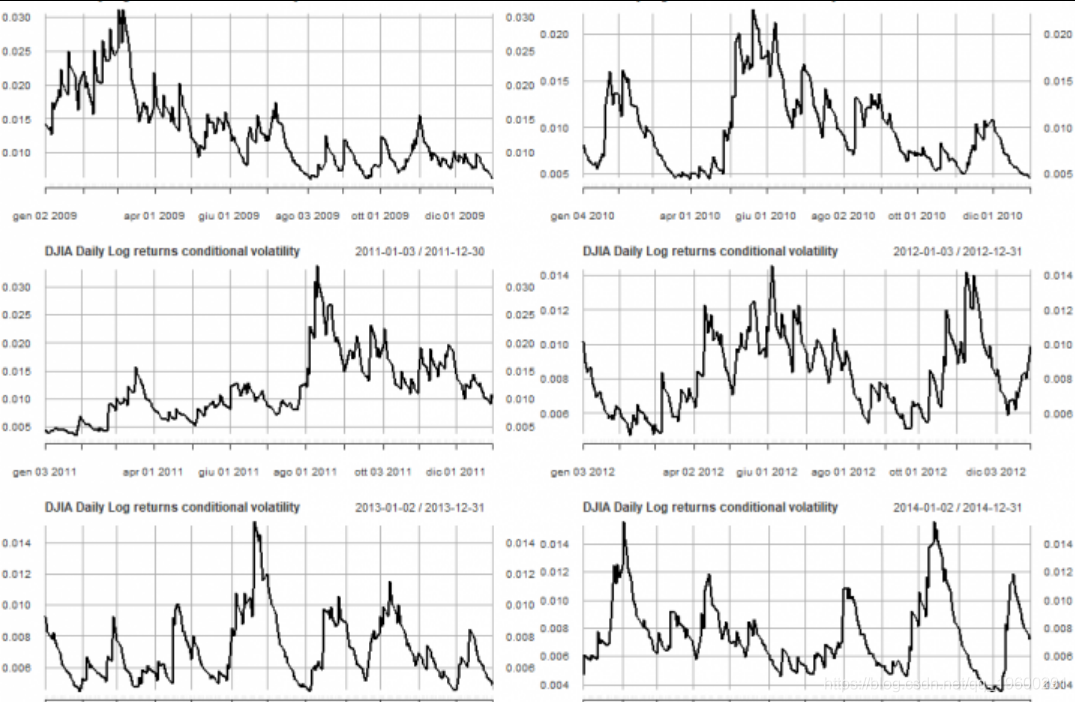
显示了按年列出的条件波动率箱图。
2008年之后,日波动率基本趋于下降。在2017年,波动率低于其他任何年。不同的是,与2017年相比,我们在2018年的波动性显着增加。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 专题:2025AI营销市场发展研究报告|附400+份报告PDF汇总下载
专题:2025AI营销市场发展研究报告|附400+份报告PDF汇总下载  专题:2025游戏科技与市场趋势报告|附130+份报告PDF汇总下载
专题:2025游戏科技与市场趋势报告|附130+份报告PDF汇总下载 Python酒店预订数据:随机森林与逻辑回归模型ROC曲线可视化
Python酒店预订数据:随机森林与逻辑回归模型ROC曲线可视化 视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析
视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析


