最近我们被客户要求撰写关于北京房价的研究报告。房价有关的数据可能反映了中国近年来的变化:
我核心的想法是预测房价。
然而,我不打算使用任何arima模型;相反,我将使用数据的特性逐年拟合回归。
- 人们得到更多的资源(薪水),期望有更好的房子
- 人口众多
- 独生子女政策:如何影响房子的几何结构?更多的卧室,更多的空间
目的
结构如下:
- 数据准备:将数值特征转换为分类;缺失值
- EDA:对于数值特征和分类特征:平均价格与这些特征的表现
- 建模:
- 分割训练/测试给定年份的数据:例如,在2000年分割数据;根据这些数据训练回归模型
- 然后,在2016年之前的所有年里,预测每套房子的价值。
- 用于验证的度量将是房屋的平均价格(即每年从测试样本中获得平均价格和预测值)
对于大多数国家来说,住房与人类生活息息相关,住房是居民总财富的重要的组成部分。易成栋、任建宇和高璇对房价和幸福感进行实证分析发现,住房会影响居民的幸福感 [1]。不仅如此,房价是支撑国民经济的重要产业,房价的波动对我国的经济的影响巨大。对房价进行合理地预测分析,有利于国家政策的调控,对相关主体产业的发展也有借鉴意义。
国内外都很重视对房价定性和定量的研究。国内外学者对于房价定性预测的研究成果比较多,如国内学者周佳琪和金百锁基于空间网络自回归变点模型对房价的影响因素进行分析,认为商业区、地铁等会影响房价 [2]。薛建谱和王卫华基于均衡分析认为引起房价上涨的主要因素是收入 [3]。范允奇和王艺明基于二阶段局部动态调整模型认为土地成本是引起房价上涨的重要因素等 [4]。但是对于房价定量预测的文献较少。在房价定量研究的文献中,Malpezzi对美国重复交易住宅价格指数用时间序列截面回归分析 [5]。国内学者邬嘉怡、王思玉、史宏炜、李虎森、楼凯达和崔丽鸿对北京房屋价格采用多小波变换进行分析 [6]。唐晓彬、张瑞和刘立新对北京二手房价格指数采用蝙蝠算法的SVR模型进行分析 [7]。
通过文献回顾可以看出国内外理论界进行房价预测的方法主要有时间序列截面回归分析等。
| [1] | 易成栋, 任建宇, 高璇. 房价、住房不平等与居民幸福感——基于中国综合社会调查2005、2015年数据的实证研究[J]. 中央财经大学学报, 2020(6): 105-117. |
| [2] | 周佳琪, 金百锁. 基于空间网络自回归变点模型的合肥市房地产价格影响因素分析[J]. 中国科学院大学学报, 2020, 37(3): 398-404. |
| [3] | 薛建谱, 王卫华. 基于均衡模型的我国商品房价格影响因素分析[J]. 统计与决策, 2013(22): 118-121. |
| [4] | 范允奇, 王艺明. 中国房价影响因素的区域差异与时序变化研究[J]. 贵州财经大学学报, 2014(1): 62-67. |
| [5] |
Malpezzi, S. (1999) A Simple Error Correction Model of House Prices. Journal of Housing Economics, 8, 27-62. https://doi.org/10.1006/jhec.1999.0240 |
| [6] | 邬嘉怡, 王思玉, 史宏炜, 李虎森, 楼凯达, 崔丽鸿. 基于多小波的北京市房屋市场价格的分析预测[J]. 北京化工大学学报(自然科学版), 2019, 46(5): 101-106. |
| [7] | 唐晓彬, 张瑞, 刘立新. 基于蝙蝠算法SVR模型的北京市二手房价预测研究[J]. 统计研究, 2018, 35(11): 71-81. |
数据准备
我们对特征有了非常完整的描述:
url:获取数据(字符)的urlid:id(字符)Lng:和Lat坐标,使用BD09协议。(数字)Cid:社区id(数字)交易时间:交易时间(字符)DOM:市场活跃日。(数字)关注者:交易后的人数。(数字)总价:(数值)价格:按平方计算的平均价格(数值)面积:房屋的平方(数字)- 起居室
:客厅数(字符) - 客厅
:客厅数(字符) 厨房:厨房数量(数字)浴室数量(字符)房子的高度建筑类型:包括塔楼(1)、平房(2)、板塔组合(3)、板(4)(数值)施工时间装修:包括其他(1)、粗(2)、简单(3)、精装(4)(数值)建筑结构:包括未清(1)、混合(2)、砖和木(3)、砖混凝土(4)、钢(5)和钢-混凝土复合材料(6)。(数值)梯梯比:同层居民数与电梯数量的比例。电梯有(1)或没有电梯(0)(数值)五年期:业主拥有不到5年的财产(数字)
数据清理、特征创建
从最初的数据看:
- 从网址上,我发现它有位置信息,如chengjiao/101084782030。同样,一个简单的regexp进行省特征提取。
- 另一个大的数据准备工作是转换一些数字特征,比如地铁,地铁站附近的房子编码为1,相反的情况编码为0。
- 还有很大一部分DOM缺失。我既不能在建模中使用这个特性,也不能删除NA,但它也会减小数据帧的大小。
#从网址中提取省份
sapply(df$url, function(x) strsplit(x,'/')[[1]][4]) 检查缺失
#缺失数据图
ggplot(data = .,aes(x = V2, y = V1)) + geom_tile(aes(fill = value )) + 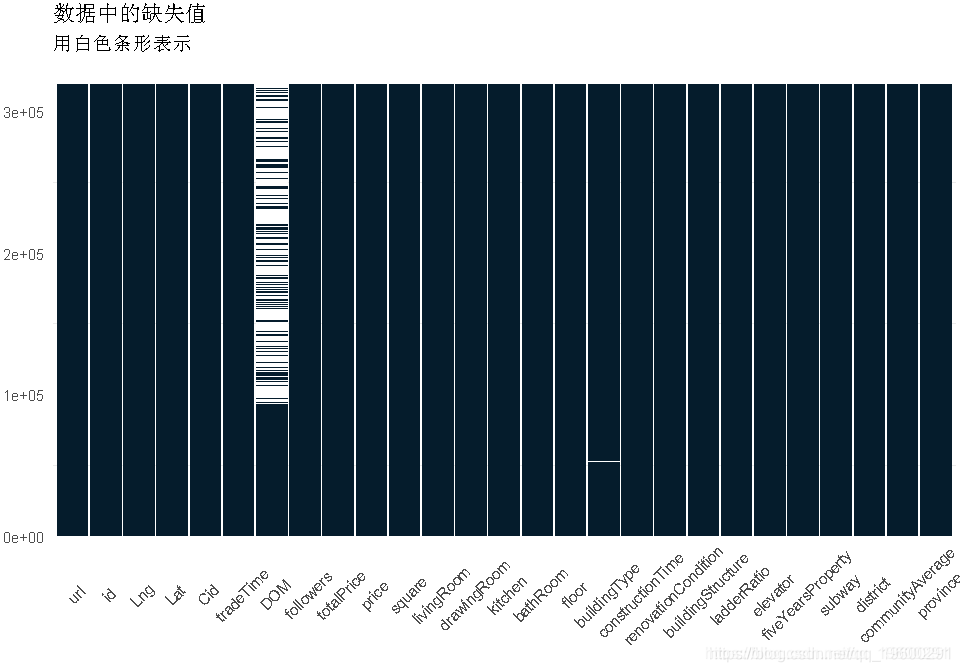
- 如上所述,DOM的很大一部分丢失了。我决定先保留这个特性,然后用中间值来填充缺失的值(分布是非常倾斜的)
- 否则,buildingType和communityAverage(pop.)中只有几个缺少的值,我决定简单地删除这些值。事实上,它们只占了约30行,而整个数据集的数据量为300k+,因此损失不会太大。
- 下面我简单地删除了我以后不打算使用的特征。
ifelse(is.na(df$DOM),median(df$DOM,na.rm=T),df$DOM) 用于将数字转换为类别的自定义函数
对于某些特征,需要一个函数来处理多个标签,对于其他一些特征(客厅、客厅和浴室),转换非常简单。
df2$livingRoom <- as.numeric(df2$livingRoom) 似乎buildingType具有错误的编码数字值:
| buildingType | count |
|---|---|
| 0.048 | 4 |
| 0.125 | 3 |
| 0.250 | 2 |
| 0.333 | 5 |
| 0.375 | 1 |
| 0.429 | 1 |
| 0.500 | 15 |
| 0.667 | 1 |
| 1.000 | 84541 |
| 2.000 | 137 |
| 3.000 | 59715 |
| 4.000 | 172405 |
| NaN | 2021 |
由于错误的编码值和NA的数量很少,因此我将再次丢弃这些行
df2$renovationCondition <- sapply(df2$renovationCondition, ionCondition)
df2$buildingStructure <- sapply(df2$buildingStructure, makeStructure)
df2$elevator <- ifelse(df2$elevator==1,'has_elevator','no_elevator') 缺失值检察
# 缺失数据图
df2 %>% is.na %>% melt %>%
ggplot(data = .,aes(x = Var2, y = Var1)) + geom_tile(aes(fill = value)) +
scale_fill_manual(values = c("grey20","white")) + theme_minimal(14) + 
kable(df %>% group_by(constructionTime) %>% summarise(count=n()) %>% arrange(-count) %>% head(5))| constructionTime | count |
|---|---|
| 2004 | 21145 |
| 2003 | 19409 |
| NA | 19283 |
| 2005 | 18924 |
| 2006 | 14854 |
df3 <- data.frame(df2 %>% na.omit())插补后的最终检查
any(is.na(df3))随时关注您喜欢的主题
## [1] FALSE探索性分析
由于有数字和分类特征,我将使用的EDA技术有:
- 数值:相关矩阵
- 分类:箱线图和地图
我们必须关注价格(单位价格/单位价格)以及总价格(百万元)
totalPrice将是回归模型的目标变量。
数值特征
corrplot(cor(
df3 ,
tl.col='black')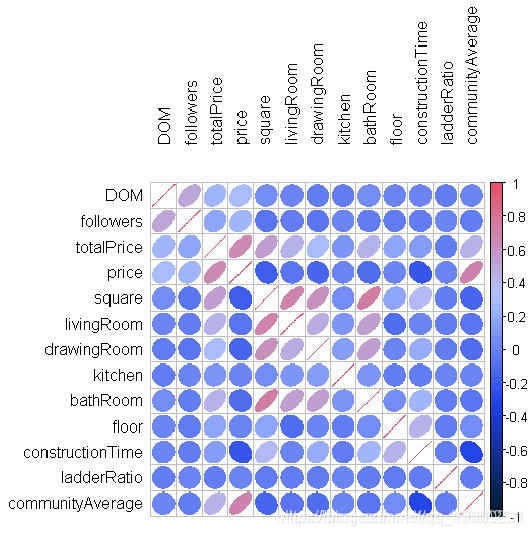
评论
- totalPrice与communityAverage有很强的正相关关系,即人口密集区的房价较高
- totalPrice与客厅、卫浴室数量有一定的正相关关系。
- 至于面积变量,我们看到它与上述变量也有很强的相关性:这是有道理的,因为如果房子的面积大,可以建造更多的房间(显而易见)。
- 其他一些有趣的相关性:communityAverage与建筑时间呈负相关,这意味着在人口密集区建房所需的时间更短
分类特征
地图
- 中国三级(省)地图
- 我看了看城郊,它位于北京附近,所以我过滤了那个特定省份的地图
ggplot() +
geom_polygon(data = shapefile_test,aes(x = long, y = lat, group = group),
BeijingLoc <- data.frame('Long'=116.4075,'Lat' = 39.904)建筑结构
makeEDA('buildingStructure' )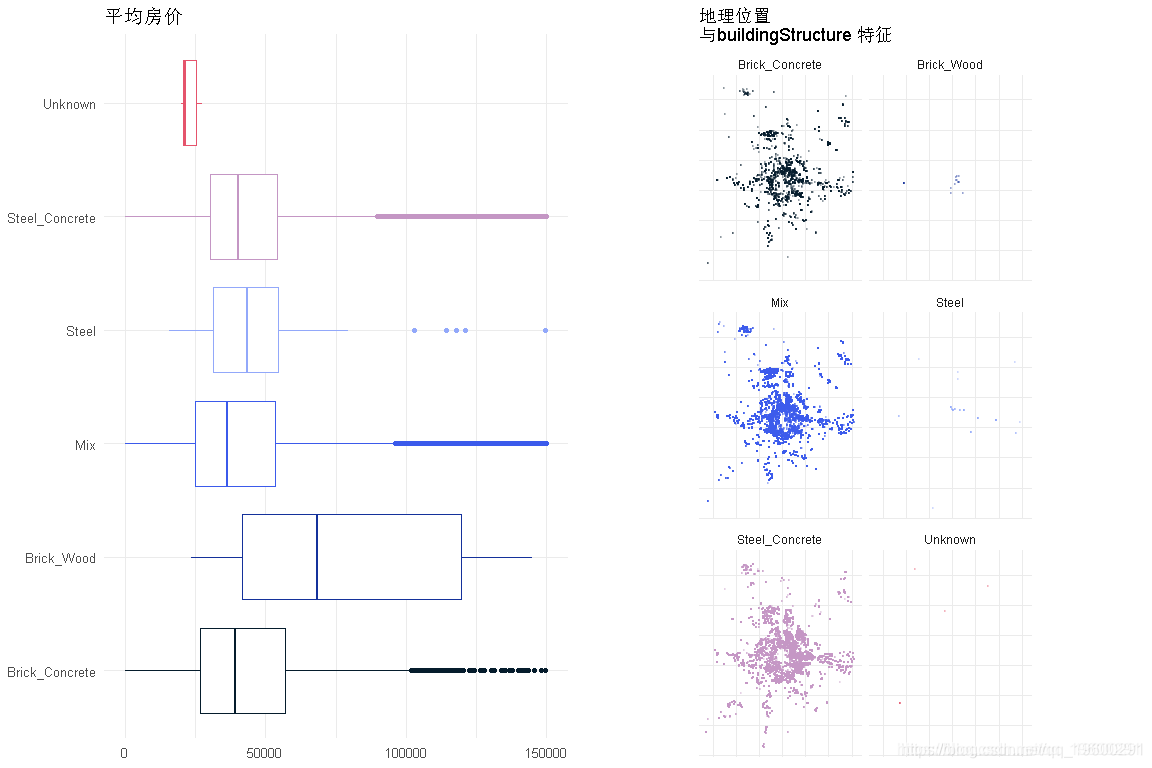
砖木结构的房屋是最昂贵的,几乎是其他类型房屋的两倍
建筑类型
makeEDA('buildingType' )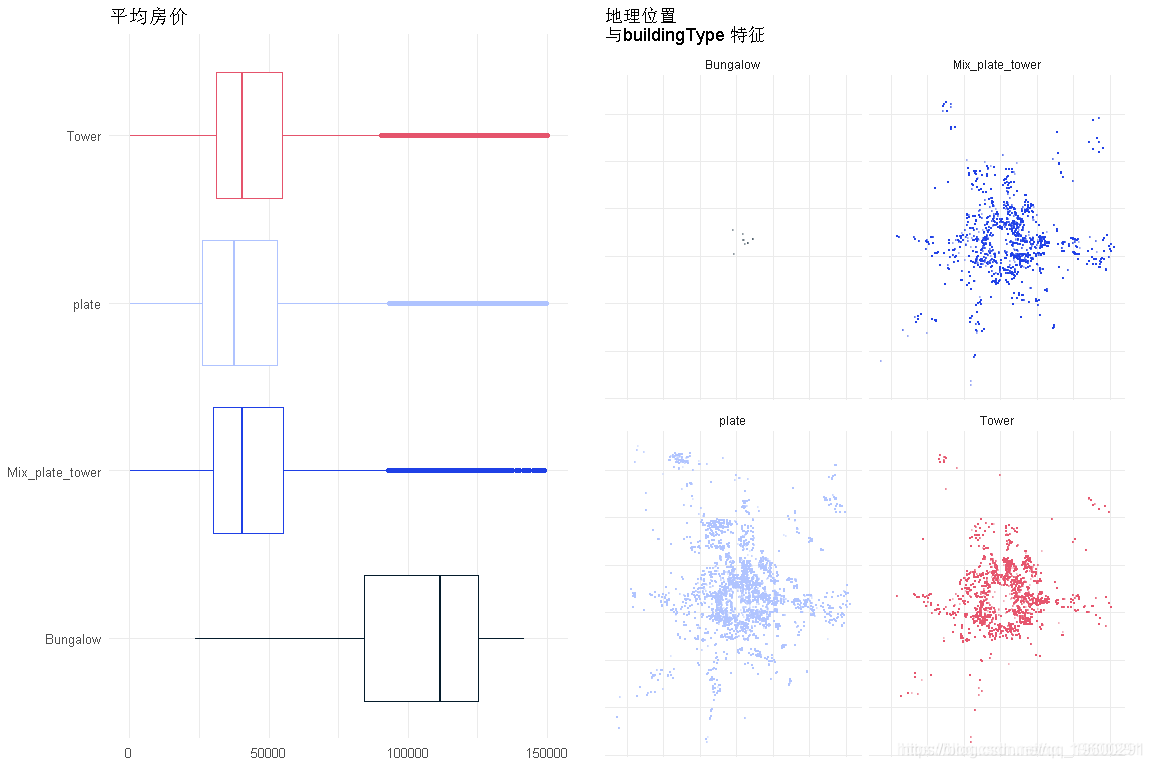
平房是最昂贵的,也是最本地化的
装修条件
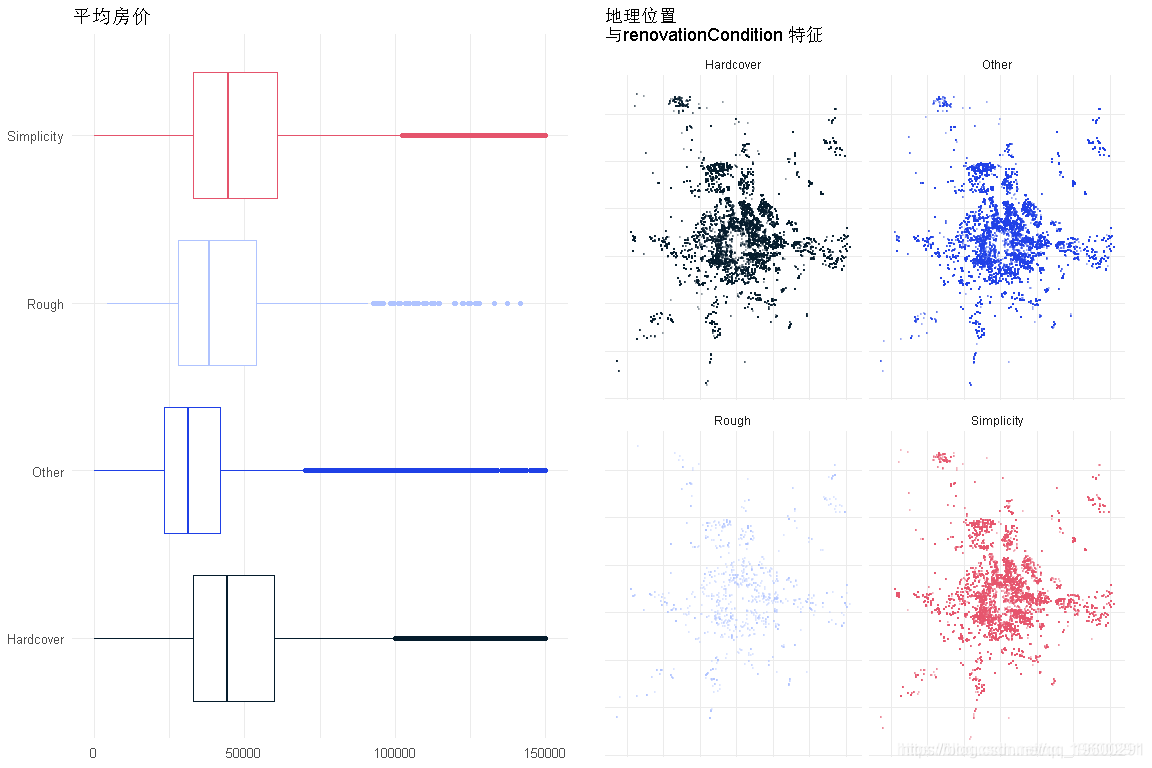
电梯
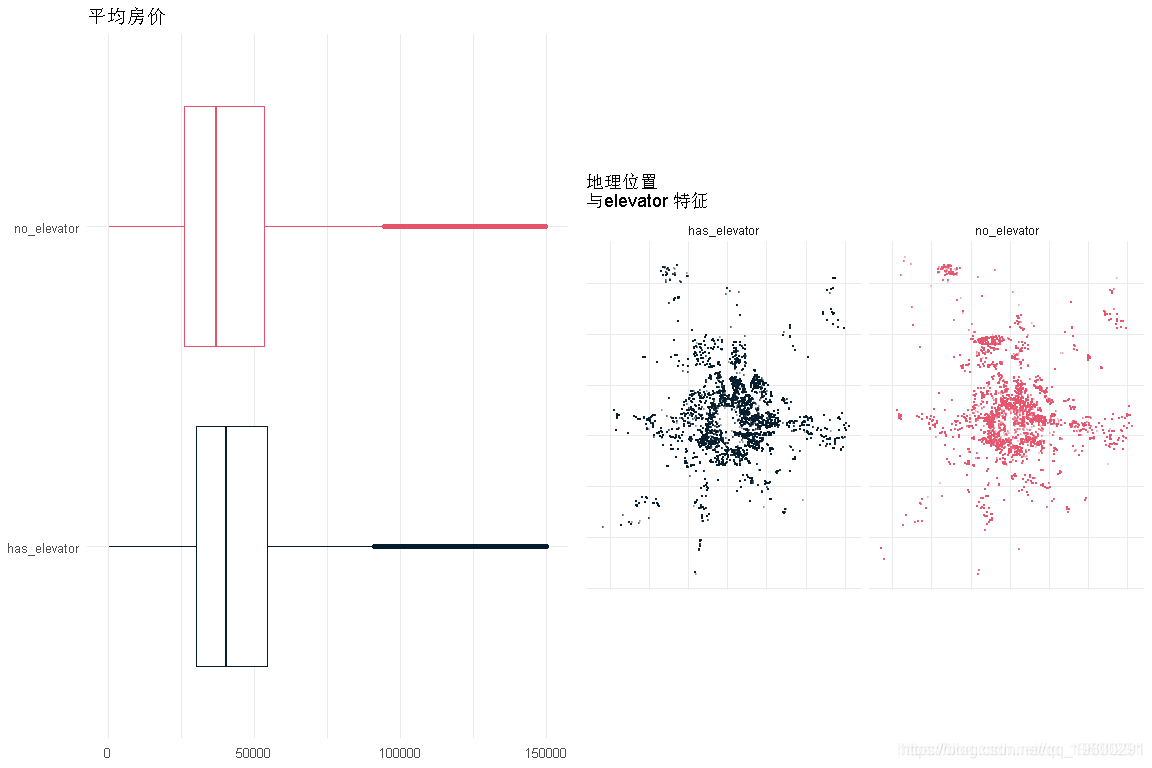
- 价格对电梯的依赖性非常小
- 住宅的分布与这一特征是相对相等的。
地铁
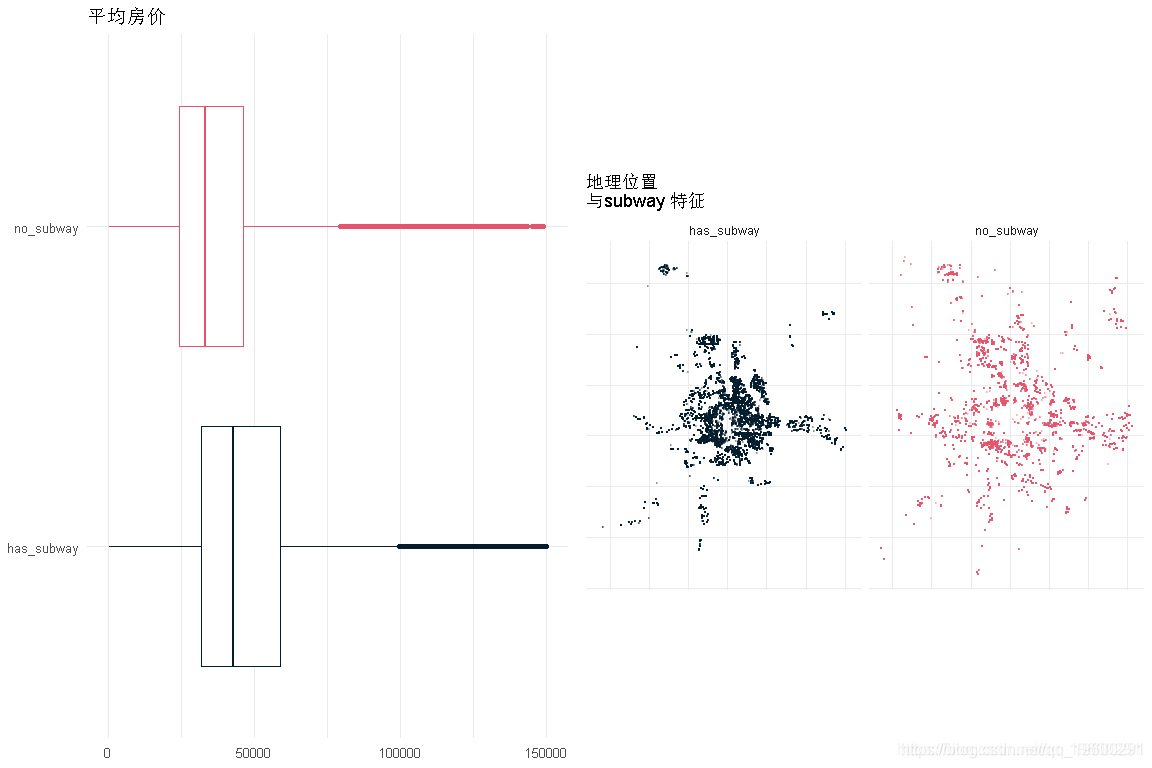
- 价格对地铁站附近的依赖性非常小。
- 住宅的分布与这一特征是相对相等的。
是否满_五年_
makeFeatureCatEDA('fiveYearsProperty', length(unique(df3$fiveYearsProperty)))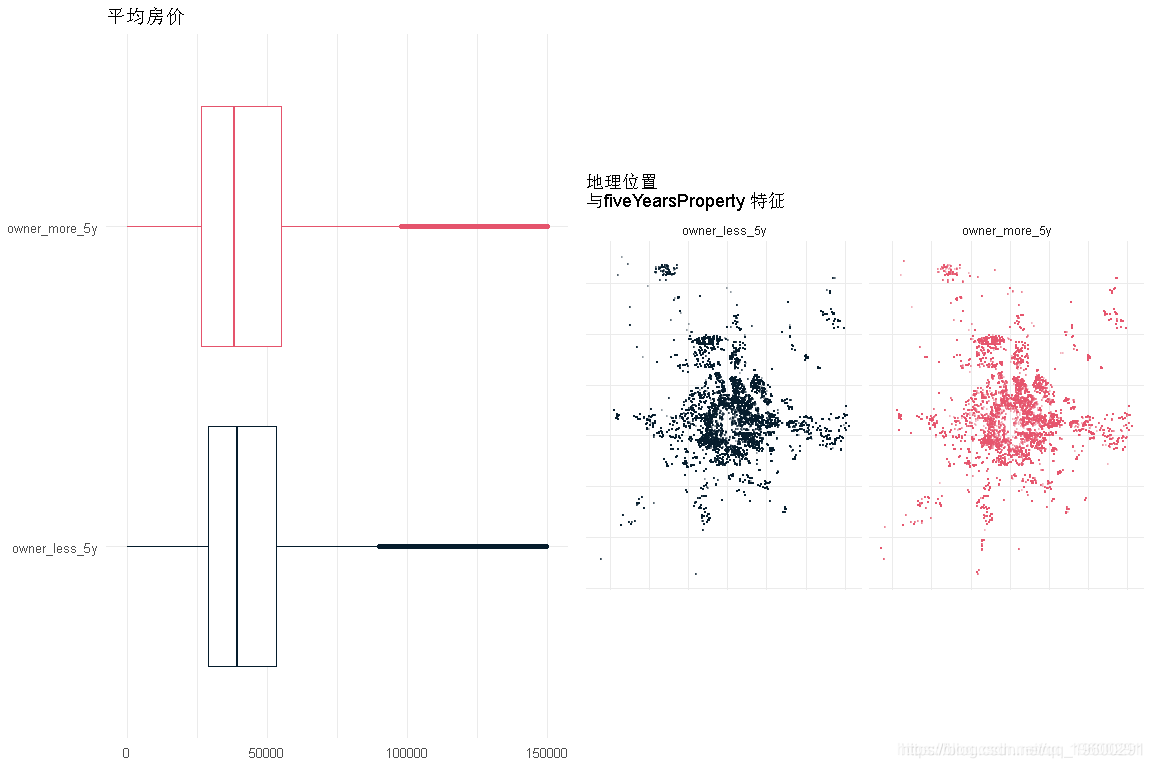
- 对于是否拥有不到5年房产来说,价格的依赖性确实很小
- 就这一特征而言,房子的分布是相对平等的
区域
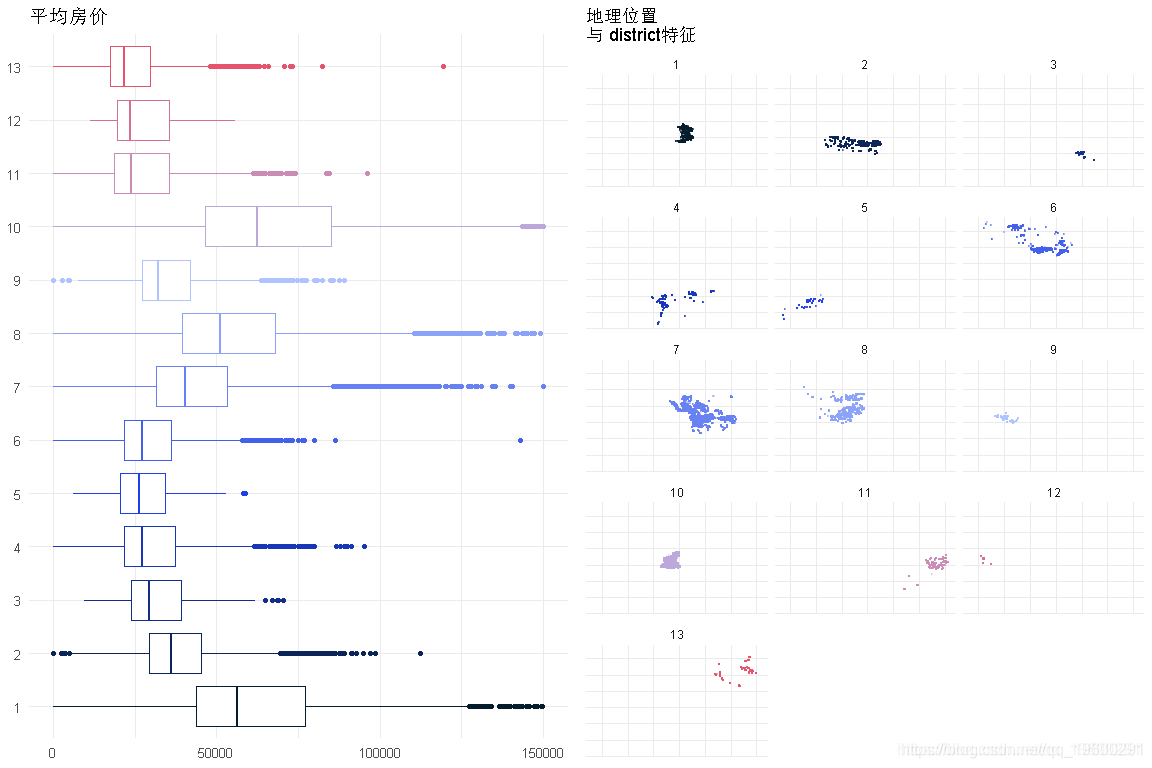
回归模型
策略
- 从tradeTime中提取年份和月份
按年度和月份分组,得到房屋的数量和均价- 拆分数据集:
- 对于年[2010-2017]=在这组年上训练并运行回归模型
- 对于>2017年:逐月对测试样本并预测平均价格
平均价格总览
首先需要看看我们想要预测什么
df3$year <- year(df3$tradeTimeTs)
df3$month <- month(df3$tradeTimeTs) df3 %>% filter(year>2009) %>% group_by(monthlyTrad) %>%
summarise(count=n(), mean = mean(price)) %>%
ggplot(aes(x=monthlyTradeTS, y= mean)) + 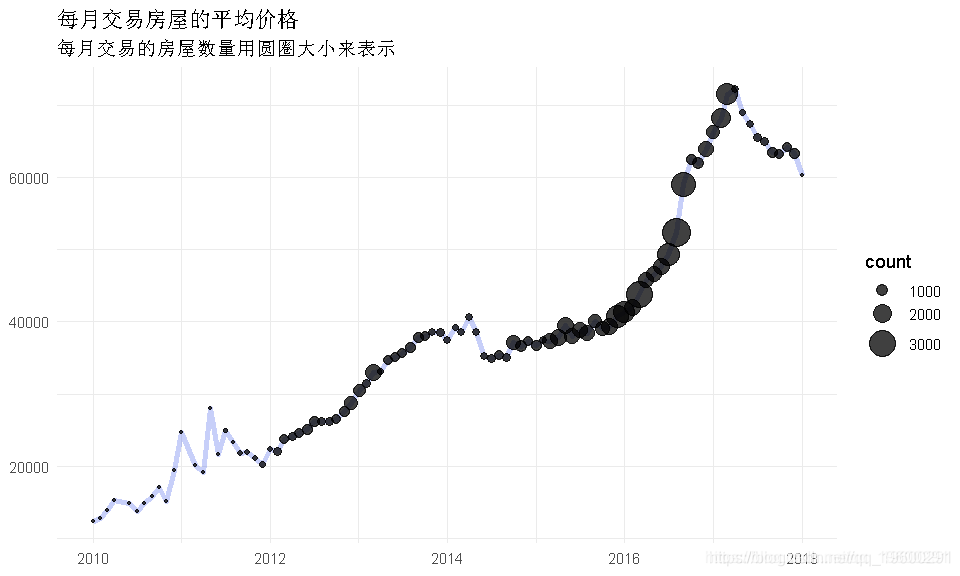
- 平均价格上涨至2017年中期,然后迅速下降
- 同时,房屋数量随着价格的上涨而增加,而且现在房屋交易的数量也随着价格的上涨而减少。
准备训练/测试样本
我在2017-01-01拆分数据。对于所有样本,我需要把分类特征变成伪变量。
df_train <- data.frame(df %>% filter(year>2009 & year<2017))
df_test <- data.frame(df %>% filter(year>=2017))
as.data.frame(cbind(
df_train %>% select_if(is.numeric) %>% select(-Lng, -Lat, -year, -month),
'bldgType'= dummy.code(df_train$buildingType),
'bldgStruc'= dummy.code(df_train$buildingStructure),
'renovation'= dummy.code(df_train$renovationCondition),
'hasElevator'= dummy.code(df_train$elevator), 在这一步中,我只训练一个线性模型
regressors<-c('lm')
Control <- trainControl(method = "cv",number = 5, repeats=3)
for(r in regressors){
cnt<-cnt+1
res[[cnt]]<-train(totalPrice ~., data = train ,method=r,trControl = Control) 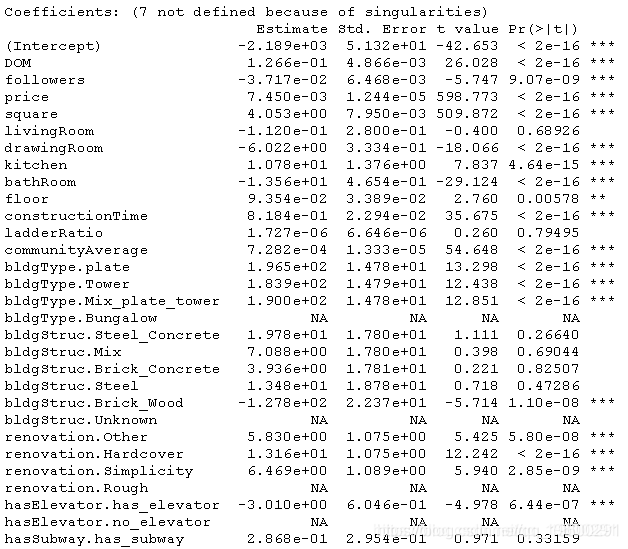

r^2在0.88左右,不错。让我们看看细节。
训练精度
g1<-ggplot(data=PRED,aes(x=Prediction,y=True)) + geom_jitter() + geom_smooth(method='lm',size=.5) +
#计算指标
mse <- mean((PRED$True-PRED$Prediction)^2)
rmse<-mse^0.5
SSE = sum((PRED$Pred - PR 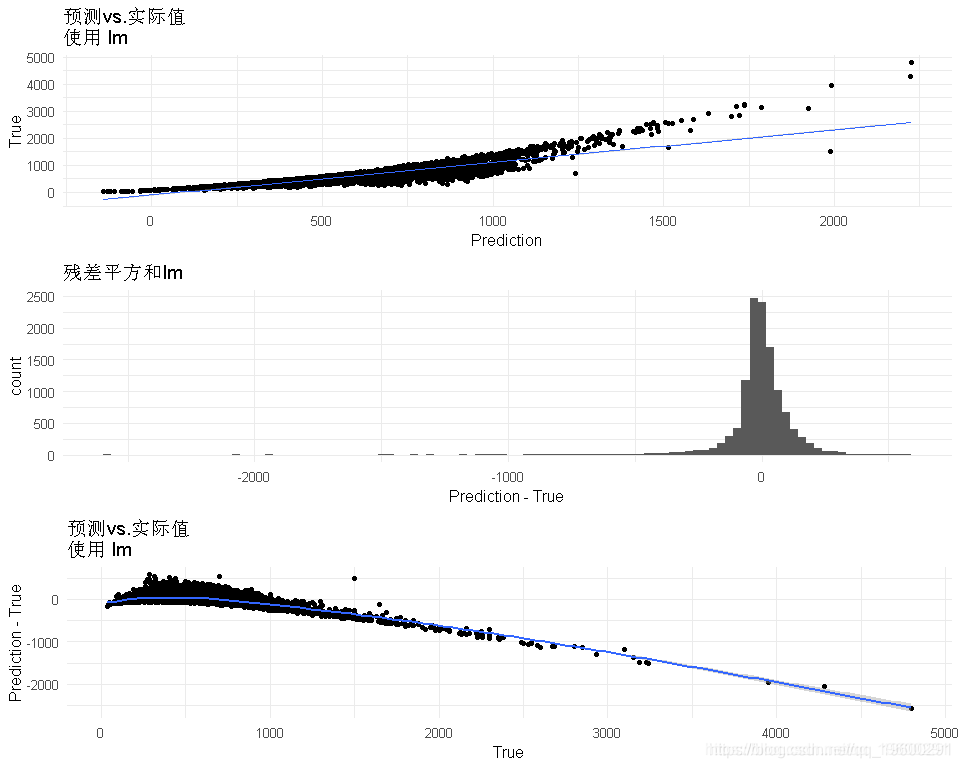
## [1] "MSE: 15952.845934 RMSE : 126.304576 R2 :0.795874"- 所以看起来残差还不错(分布是正态的,以0为中心),但对于低价格来说似乎失败了。训练和测试样本的预测与时间的关系
- 基本上与上述相同,但我将重复预测所有月份的训练数据
- 我的目标指标是平均房价。
- 训练是在10多年的训练样本中完成的,因此逐月查看预测将非常有趣。
# 训练样本->训练精度
for (i in 1:length(dates_train)){
current_df <- prepareDF(current_df)
current_pred <- mean(predict(res[[1]],current_df))
#运行测试样本-->测试精度
for (i in 1:length(dates_test)){
current_df <- prepareDF(current_df)
current_pred <- mean(predict(res[[1]],current_df)) RES %>% reshape2::melt(id=c('date','split')) %>%
ggplot(aes(x=date,y=value)) + geom_line(aes(color=variable, lty=split),size=1) + 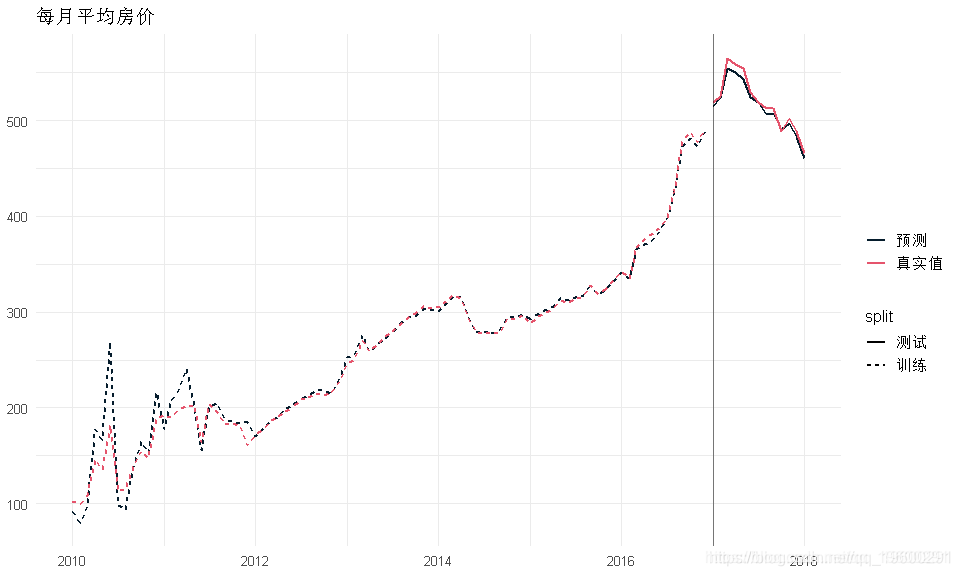
- 预测对于2012年之后的数据确实非常好,这可能与有足够数据的月份相对应
改进
地理位置作为特征
- 下面是一个有趣的图;它显示了每个位置的总价格。 在二维分布的中心,价格更高。
- 这个想法是计算每个房子到中心的距离,并关联一个等级/分数
BeijingLoc <- data.frame('Long'=116.4075,'Lat' = 39.904)
df3 %>% ggplot(aes(x=Lng,y=Lat)) + geom_point(aes(color=price),size=.1,alpha=.5) +
theme(legend.position = 'bottom') + 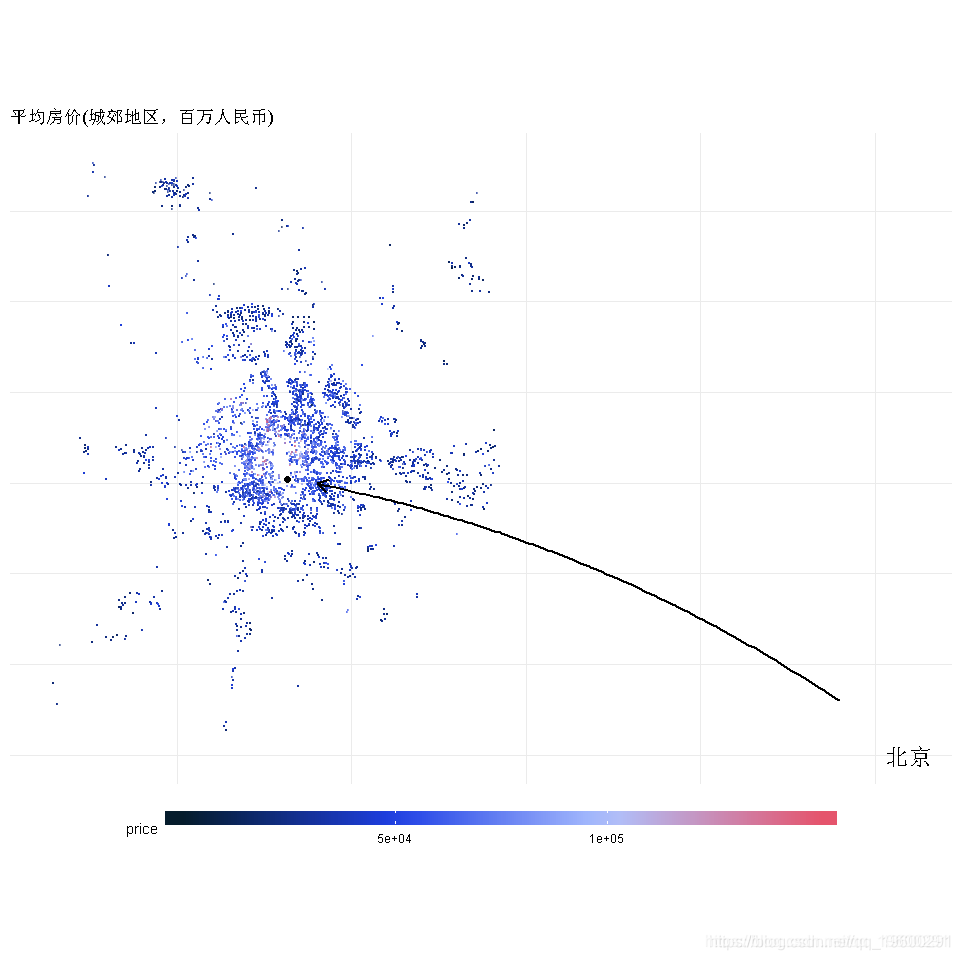
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!



 Python酒店预订数据:随机森林与逻辑回归模型ROC曲线可视化
Python酒店预订数据:随机森林与逻辑回归模型ROC曲线可视化 Python用Transformer、SARIMAX、RNN、LSTM、Prophet时间序列预测对比分析用电量、零售销售、公共安全、交通事故数据
Python用Transformer、SARIMAX、RNN、LSTM、Prophet时间序列预测对比分析用电量、零售销售、公共安全、交通事故数据 Python谷歌商店Google Play APP评分预测:LASSO、多元线性回归、岭回归模型对比研究
Python谷歌商店Google Play APP评分预测:LASSO、多元线性回归、岭回归模型对比研究 Python+AI提示词出租车出行轨迹:梯度提升GBR、KNN、LR回归、随机森林融合预测及贝叶斯概率异常检测研究
Python+AI提示词出租车出行轨迹:梯度提升GBR、KNN、LR回归、随机森林融合预测及贝叶斯概率异常检测研究


