在最近的一篇文章中，我描述了一个Metropolis-in-Gibbs采样器，用于估计贝叶斯逻辑回归模型的参数。
这篇文章就此问题进行了研究，以展示Rcpp如何帮助克服这一瓶颈。 TLDR：只需用C ++编写log-posterior而不是矢量化R函数，我们就可以大大减少运行时间。
可下载资源
我模拟了模型的数据：
×
MH算法在参数空间随机取值，作为起始点。按照参数的概率分布生成随机的参数，按照这一系列参数的组合，计算当前点的概率密度。依据当前点和起始点概率密度比值是否大于(0,1)之间的随机数来判断是否保留当前点。若当前点的概率密度大于该随机数，就称这种状态为接受状态，此时，在满足参数概率分布的前提下，继续随机抽取参数的组合，作为下一点，计算下一点的概率密度，并计算下一点概率密度和概率密度的比值，并继续循环。若当前点不能被接受，则继续在满足参数概率分布的前提下，继续生成随机数，作为新的参数组合，直到参数组合能够被接受为止。
下面是用MCMC MH抽样法生成满足一定条件二元正态分布的例子。
问题：## 对于一个二元正态分布，给定输入数据点向量x （x包含两个元素，x1，x2）， 平均值参数向量mu（x1，x2），和sigma（方差矩阵），写出二元正态分布的概率密度函数。
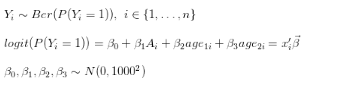
对于这个分析，我编写了两个Metropolis-Hastings（MH）采样器：sample\_mh（）和sample\_mh\_cpp（）。
视频
贝叶斯推断线性回归与R语言预测工人工资数据
视频
逻辑回归Logistic模型原理和R语言分类预测冠心病风险实例
前者使用对数后验编码作为向量化R函数。后者使用C ++（log\_post.cpp）中的log-posterior编码，并使用Rcpp编译成R函数。Armadillo库对C ++中的矩阵和向量类很有用。
因此，在每次迭代中，提出了系数向量。下面用红线表示链，表示生成数据的参数值。
burnin <- 1000 iter <- 100000 p <- ncol(X) cpp(X, Y, iter = iter, jump = .03) par(mfrow=c(2,2)) plot(mh_cpp\[\[1\]\]\[burnin:iter,'intercept'\]) abline(h= -1, col='red')
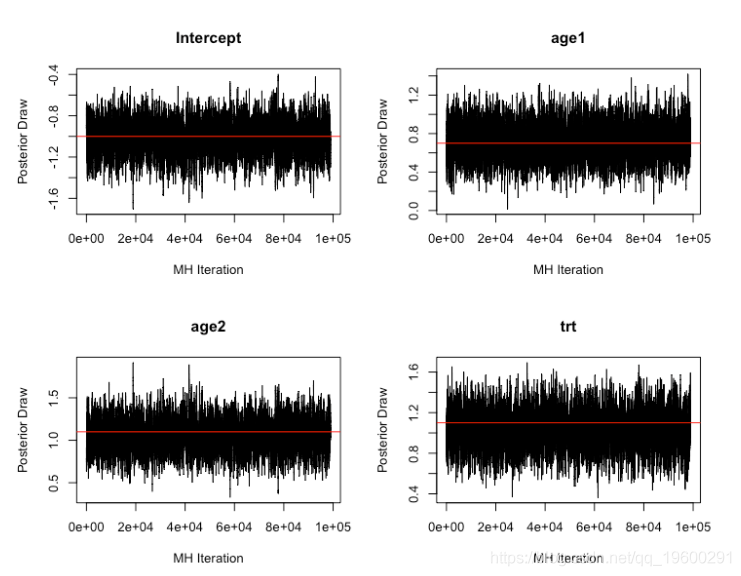
似乎趋同。平均接受概率在采样运行中收敛到约20％。
那么Rcpp实现与R实现相比如何呢？Rcpp的运行时间明显较低。当log-posterior被编码为矢量化R函数时，采样器相对于Rcpp实现运行速度大约慢7倍（样本大小为100）。下图显示了样本大小为100到5000的相对运行时间，增量为500。
for(i in 1:length(s){
benchmark(mh(X, Y, iter = iter)
time\[i\] <- time/rcpp
plot(ss, time)
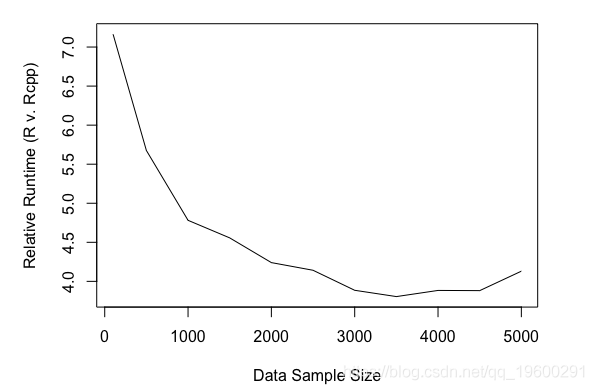
直观地说，C ++带来了一些效率增益。但很明显，Rcpp是解决代码瓶颈的好方法。
数据代码分享|R语言回归分析：体脂数据、公交绿色出行与全球变暖2案例
R语言武汉流动人口趋势预测：灰色模型GM（1，1）、ARIMA时间序列、logistic逻辑回归模型
R语言bnlearn包：贝叶斯网络的构造及参数学习的原理和实例|视频课程
R语言K-Means(K-均值)聚类、朴素贝叶斯（Naive Bayes）模型分类可视化
